7. Власний, інваріантний та циклічний підпростори лінійного оператора

Нехай лінійний оператор у векторному просторі над полем має в деякому базисі матрицю .

Означення. Власним вектором оператора називається такий ненульовий вектор 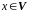, який цим оператором переводиться в пропорційний йому вектор , тобто , де – деяке число з поля , яке називається власним значенням оператора .

Теорема. Власними значеннями лінійного оператора , який діє у векторному просторі над полем є характеристичні корені цього оператора, які належать полю .

Для знаходження всіх власних значень оператора з матрицею треба знайти всі характеристичні числа матриці і з них вибрати тільки ті, які належать полю . Для знаходження всіх власних векторів оператора з матрицею для кожного власного значення треба знайти всі ненульові розв’язки системи .

Теорема. Множина власних векторів лінійного оператора , які відповідають власному значенню , разом з нульовим вектором утворює лінійний підпростір векторного простору .

Означення. Власним підпростором, що відповідає власному значенню оператора називається підпростір , утворений власними векторами, які відповідають власному значенню .

За означенням . Якщо оператор в заданому базисі має матрицю , то .

Приклад. Знайти власні значення, власні вектори і власні підпростори лінійного оператора у дійсному векторному просторі, який в заданому базисі має матрицю:

.

Розв’язання. Щоб знайти власні значення, обчислюємо характеристичний многочлен матриці

.

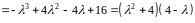Він має корені і . Оскільки розглядається оператор у дійсному векторному просторі, то його власним значенням буде тільки .

Зайдемо власні вектори, що відповідають значенню . При система набуває вигляду:

,

або

.

Для знаходження загального розв’язку цієї системи скористаємося методом Гаусса.

Невідомі , – базисні, невідоме – вільне. Виразимо базисні невідомі через вільне.

Вільному невідомому можна надавати будь-яких значень. Нехай , де . Тоді загальний розв’язок системи , , або у вигляді матриці-рядка 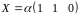. При загальний розв’язок дає всі власні вектори лінійного оператора з матрицею .

Власним підпростором, що відповідає власному значенню лінійного оператора з матрицею буде одновимірний підпростір . Вектор є базисом підпростору .

Власний підпростір є окремим випадком інваріантного підпростору лінійного оператора .

Означення. Інваріантним підпростором лінійного оператора називається такий підпростір 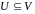, що образом кожного вектора з є вектор, який знову належить , тобто .

Інваріантні підпростори мають наступні важливі властивості.

1. Якщо мінімальний многочлен матриці має вид , де , 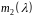– нормовані, взаємно прості многочлени, то простір розкладається на два інваріантні підпростори , : , причому мінімальними многочленами цих підпросторів є відповідно та .

2. У просторі завжди існує вектор , мінімальний многочлен якого збігається з мінімальним многочленом всього простору .

Означення. Циклічним підпростором лінійного оператора називається інваріантний підпростір з базисом виду . Вектор називається твірним вектором циклічного підпростору.

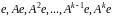Мінімальний многочлен такого підпростору має степінь , оскільки вектори обов’язково будуть лінійно залежними.

Циклічні підпростори мають наступні властивості.

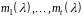1. Простір розкладається на циклічні відносно лінійного оператора підпростори : , з мінімальними многочленами таким чином, що збігається з мінімальним многочленом всього простору і .

2. Лінійний простір циклічний (відносно оператора ) тоді і тільки тоді, коли розмірність простору збігається зі степенем його мінімального многочлена.

3. Циклічний лінійний простір розкладається тільки на циклічні інваріантні підпростори, причому мінімальні многочлени цих підпросторів взаємно прості.

4. Лінійний простір можна розкласти на циклічні підпростори таким чином, що мінімальний многочлен кожного з них є степенем незвідного над полем многочлена.