4. Координати вектора у векторному просторі. Розкладання вектора за базисом

Для того, щоб вектори з векторного простору можна було б задавати за допомогою чисел і зводити операції над векторами до операцій над числами, вводиться поняття координат вектора.

Нехай – деякий базис векторного простору . Тоді будь-який вектор можна подати у вигляді (1)

де – деякі дійсні числа, причому єдиним чином. В цьому випадку вираз (1) називається розкладом вектора за базисом .

Означення. Коефіцієнти розкладу (1) називаються координатами вектора в даному базисі. Упорядкований набір координат вектора називається його координатним рядком і позначається :

.

Таким чином, базис дає змогу кожен вектор однозначно зобразити рядком чисел – координат цього вектора. Це зображення дозволяє виконувати над векторами лінійні операції за правилами лінійних операцій над матрицями-рядками:

якщо і в деякому базисі, то

,

.

Зауваження. Разом із координатними рядками можна розглядати координатні стовпці , отримані транспонуванням -матриці

Приклад. Довести, що вектори утворюють базис у просторі та знайти координати вектора в цьому базисі.

, , ,

Розв’язання. 1) Перевіримо необхідну і достатню умову компланарності векторів :

.

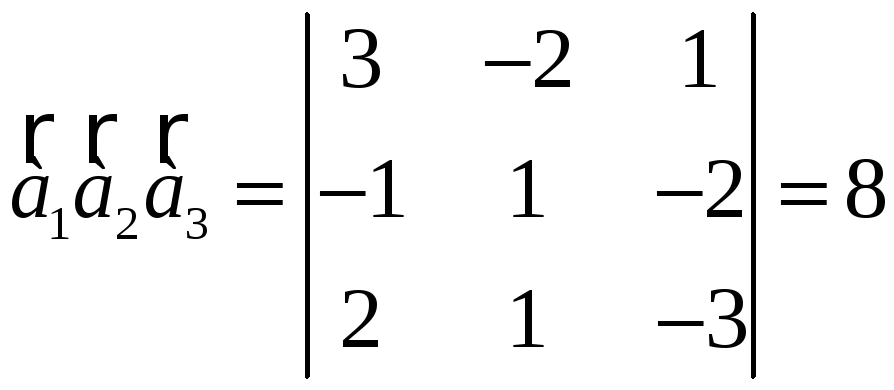Оскільки , то вектори некомпланарні, тому вони лінійно незалежні і утворюють базис.

2) Розкладемо вектор за базисом :

або в координатному вигляді:

Вектори рівні, коли їх відповідні координати рівні. Тому одержимо систему :

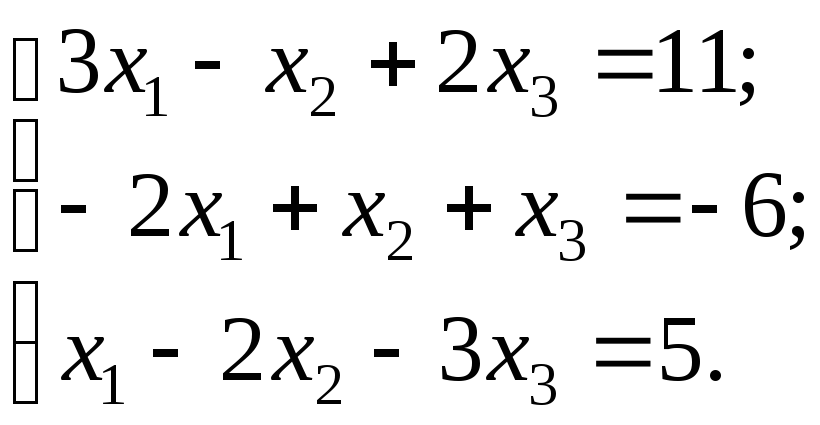
Розв’язуючи цю систему будь-яким способом, знайдемо

, , .

3) Отже, .

.

Відповідь:

4. Векторні простори із скалярним добутком

До цього часу ми розглядали властивості векторного простору, зв’язані тільки з двома операціями: додаванням векторів і множенням їх на числа. Розглянемо ще одну операцію.

Означення. Кажуть, що в векторному просторі визначена операція скалярного добутку векторів, якщо кожній парі векторів ставиться у відповідність число так, що виконані наступні умови (аксіоми скалярного множення):

,

1) ;

2) ;

3) ;

4) , .

Приклади векторних просторів із скалярним добутком.

1) У векторному просторі геометричних векторів операцію скалярного добутку визначимо формулою: для та

.

Відомо, що так визначена операція скалярного добутку задовольняє умовам 1)-4), тобто є скалярним множенням у розумінні даного означення.

2) В арифметичному числовому векторному просторі скалярний добуток визначимо формулою: для та

,

Легко перевірити, що аксіоми 1)–4) будуть виконані.

3) У векторному просторі функцій, неперервних на інтервалі визначимо скалярне множення векторів і формулою

.

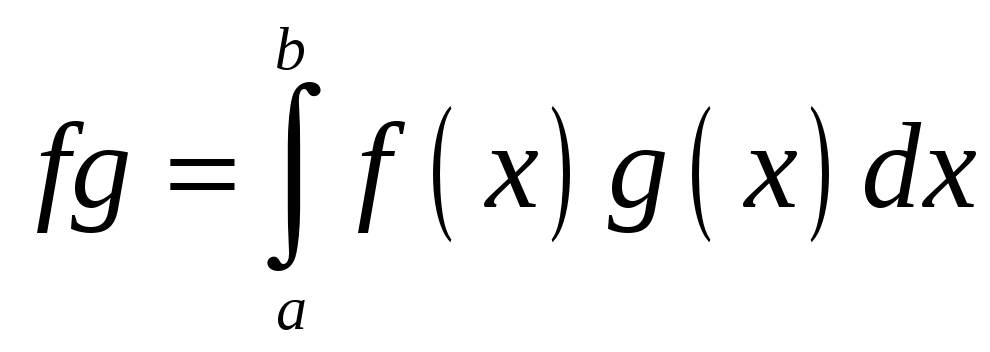З відомих властивостей визначеного інтеграла випливає, що так визначене скалярне множення задовольняє умовам 1)-4).

Означення. Евклідовим простором називається дійсний векторний простір із скалярним добутком.

Приклади.

1) Дійсний векторний простір геометричних векторів із звичайним скалярним множенням є евклідовим.

2) Арифметичний числовий векторний простір із скалярним добутком, визначеним формулою: для та

,

є евклідовим.

3) Векторний простір функцій, неперервних на інтервалі скалярним добутком векторів і , визначеним формулою

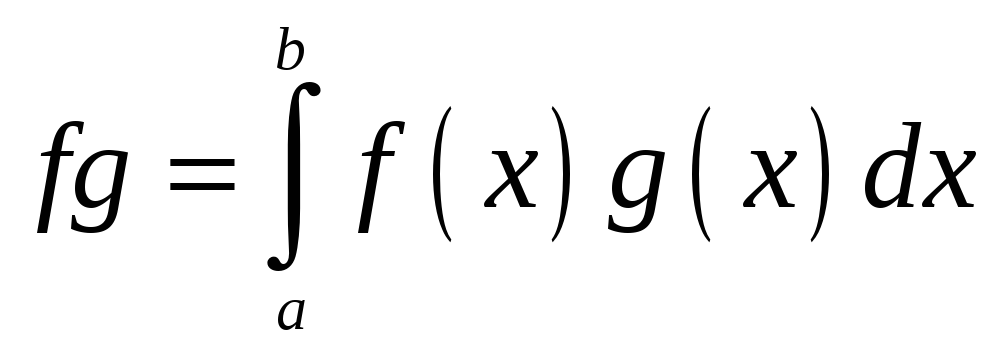
є евклідовим.