
- •Лекція 5 Тема: Векторні простори. Алгебри
- •2. Поняття, приклади і найпростіші властивості векторного простору
- •3. Лінійна залежність системи векторів. Базис і розмірність векторного простору Означення. Лінійною комбінацією векторів векторного простору називається вектор вигляду
- •4. Координати вектора у векторному просторі. Розкладання вектора за базисом
- •2) Розкладемо вектор за базисом :
- •Розв’язуючи цю систему будь-яким способом, знайдемо
- •4. Векторні простори із скалярним добутком
- •5. Підпростори векторного простору
- •6. Лінійний оператор та його матриця
- •6. Поняття алгебри. Приклади алгебр
- •8. Ізоморфізм та гомоморфізм алгебр
Лекція 5 Тема: Векторні простори. Алгебри
План лекції:
-
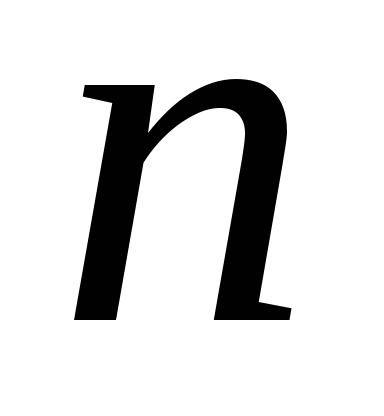 -вимірний
арифметичний простір.
-вимірний
арифметичний простір. -
Поняття, приклади і найпростіші властивості векторного простору.
-
Лінійна залежність системи векторів. Базис і розмірність векторного простору.
-
Координати вектора у векторному просторі. Розкладання вектора за базисом.
-
Підпростори векторного простору.
-
Лінійний оператор і його матриця
-
Поняття алгебри. Приклади алгебр.
-
Ізоморфізм та гомоморфізм алгебр.
1.
![]() -вимірний
арифметичний простір
-вимірний
арифметичний простір
Нехай
![]() – деяке числове поле. Числа з
– деяке числове поле. Числа з
![]() будемо позначати малими латинськими
буквами.
будемо позначати малими латинськими
буквами.
Означення.
Будь-який впорядкований набір з
![]() чисел
чисел
![]() з поля
з поля
![]() називається
називається
![]() -вимірним
числовим вектором. Числа
-вимірним
числовим вектором. Числа
![]() називаються координатами
або компонентами
вектора. Позначається
називаються координатами
або компонентами
вектора. Позначається
![]() .
.
Компоненти вектора розташовують в рядок:
![]()
або в стовпчик
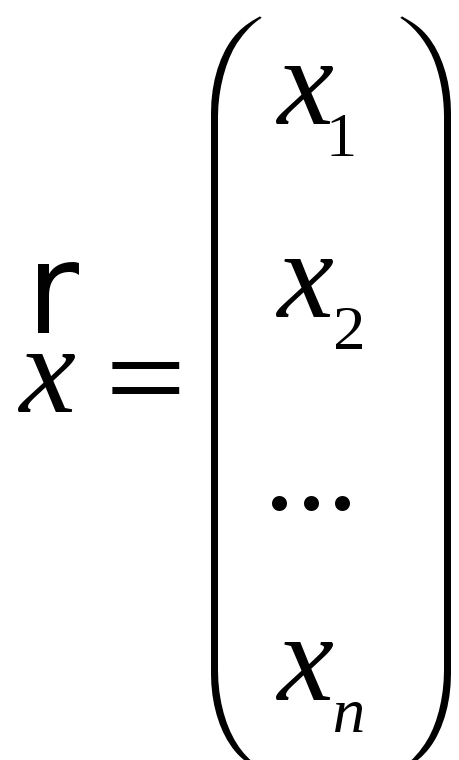 .
.
![]() -вимірний
вектор, всі компоненти якого дорівнюють
нулю, називається
нульовим або нуль-вектором:
-вимірний
вектор, всі компоненти якого дорівнюють
нулю, називається
нульовим або нуль-вектором:
![]() .
.
Означення.
Два числових вектори
![]() та
та
![]() рівні
тоді і тільки тоді, коли рівні їх
відповідні компоненти:
рівні
тоді і тільки тоді, коли рівні їх
відповідні компоненти:
![]() .
.
Відзначимо, що два числових вектори не можуть бути рівні, якщо число компонент в них неоднакове.
Позначимо
через
![]() множину всіх
множину всіх
![]() -вимірних
числових векторів з компонентами з
-вимірних
числових векторів з компонентами з
![]() .
Визначимо в цій множині операції
додавання векторів і множення вектора
на число з поля
.
Визначимо в цій множині операції
додавання векторів і множення вектора
на число з поля
![]() .
.
Означення.
Сумою векторів
![]() та
та
![]() називається вектор
називається вектор
![]() .
.
Означення.
Добутком
вектора
![]() на
число
на
число
![]() називається вектор
називається вектор
![]() .
.
Неважко
переконатися в тому, що множина
![]() всіх
всіх
![]() -вимірних
числових векторів є абелевою групою
відносно додавання. Дійсно, оскільки
операція додавання
-вимірних
числових векторів є абелевою групою
відносно додавання. Дійсно, оскільки
операція додавання
![]() -вимірних
числових векторів зводиться до додавання
їх відповідних координат, то вона
асоціативна:
-вимірних
числових векторів зводиться до додавання
їх відповідних координат, то вона
асоціативна:
1.
![]()
![]() – асоціативність додавання;
– асоціативність додавання;
і комутативна:
2.
![]()
![]() – комутативність додавання;
– комутативність додавання;
в множині
![]() міститься нульовий елемент, ним є
нуль-вектор
міститься нульовий елемент, ним є
нуль-вектор
![]() :
:
3.
![]()
![]() :
:
![]() – існування нульового елемента ;
– існування нульового елемента ;
для
кожного
![]() -вимірного
числового вектора в множині
-вимірного
числового вектора в множині
![]() міститься протилежний йому вектор
міститься протилежний йому вектор
![]() :
:
4.
![]()
![]() :
:![]() – існування протилежного елемента;
– існування протилежного елемента;
З
означення добутку вектора
![]() на число
на число
![]() випливає, що операція множення вектора
на число асоціативна:
випливає, що операція множення вектора
на число асоціативна:
5.
![]()
![]()
![]() – асоціативність множення на число;
– асоціативність множення на число;
6.
![]()
![]() .
.
Крім того, мають місце
7.
![]()
![]()
![]() – дистрибутивність множення на число
відносно додавання чисел ;
– дистрибутивність множення на число
відносно додавання чисел ;
8.
![]()
![]()
![]() – дистрибутивність множення на число
відносно додавання елементів.
– дистрибутивність множення на число
відносно додавання елементів.
Означення.
Множина
![]() всіх
всіх
![]() -вимірних
числових векторів з компонентами з поля
-вимірних
числових векторів з компонентами з поля
![]() разом з введеними операціями додавання
векторів і множення вектора на число з
поля
разом з введеними операціями додавання
векторів і множення вектора на число з
поля
![]() ,
для яких виконуються всі властивості
лінійних дій над векторами, називається
,
для яких виконуються всі властивості
лінійних дій над векторами, називається
![]() -вимірним
арифметичним простором
над полем
-вимірним
арифметичним простором
над полем
![]() .
.
2. Поняття, приклади і найпростіші властивості векторного простору
У різних розділах математики лінійні операції виконуються не тільки над векторами, а й над різними іншими об’єктами: матрицями, функціями, многочленами, тощо. Можливість підходити до цих об’єктів із загальної точки зору дає поняття векторного (лінійного) простору.
Нехай
![]() – непорожня множина елементів будь-якої
природи, які будемо позначати
– непорожня множина елементів будь-якої
природи, які будемо позначати
![]() і нехай
і нехай
![]() – деяке поле, елементи якого будемо
позначати
– деяке поле, елементи якого будемо
позначати
![]() .
Визначимо в множині
.
Визначимо в множині
![]() операцію додавання елементів:
операцію додавання елементів:
![]()
![]() і операцію множення елемента на число
з поля
і операцію множення елемента на число
з поля
![]() :
:
![]()
![]()
![]() .
.
Означення.
Множина
![]() називається векторним
(лінійним)
простором,
якщо в
називається векторним
(лінійним)
простором,
якщо в
![]() визначені алгебраїчна операція додавання
і операція множення на числа з поля
визначені алгебраїчна операція додавання
і операція множення на числа з поля
![]() ,
причому виконані наступні умови (аксіоми
векторного простору):
,
причому виконані наступні умови (аксіоми
векторного простору):
1.
![]()
![]() – асоціативність додавання;
– асоціативність додавання;
2.
![]()
![]() – комутативність додавання ;
– комутативність додавання ;
3.
![]()
![]() :
:
![]() – існування нульового елемента ;
– існування нульового елемента ;
4.
![]()
![]() :
:![]() – існування протилежного елемента;
– існування протилежного елемента;
5.
![]()
![]()
![]() – асоціативність множення на число;
– асоціативність множення на число;
6.
![]()
![]() .
.
7.
![]()
![]()
![]() – дистрибутивність відносно додавання
чисел ;
– дистрибутивність відносно додавання
чисел ;
8.
![]()
![]()
![]() – дистрибутивність відносно додавання
елементів;
– дистрибутивність відносно додавання
елементів;
Елементи
векторного простору називаються
векторами,
елемент
![]() називається
нульовим вектором (нуль-вектором).
називається
нульовим вектором (нуль-вектором).
Будемо
позначати векторний простір, визначений
на множині
![]() через
через
![]() або
або
![]()
![]() .
Якщо поле
.
Якщо поле
![]() є поле дійсних чисел
є поле дійсних чисел
![]() ,
то векторний простір
,
то векторний простір
![]() називається дійсним
векторним простором; якщо
поле
називається дійсним
векторним простором; якщо
поле
![]() є полем комплексних чисел, то векторний
простір
є полем комплексних чисел, то векторний
простір
![]() називається комплексним
векторним простором.
називається комплексним
векторним простором.
Приклади векторних просторів:
1) Множина
![]() дійсних чисел із звичайними операціями
додавання і множення є дійсним векторним
простором. Множина
дійсних чисел із звичайними операціями
додавання і множення є дійсним векторним
простором. Множина
![]() комплексних чисел відносно операцій
додавання комплексних чисел і множення
комплексних чисел на дійсні числа є
дійсний векторний простір
комплексних чисел відносно операцій
додавання комплексних чисел і множення
комплексних чисел на дійсні числа є
дійсний векторний простір
![]() .
.
2)
![]() -вимірний
арифметичний простір
-вимірний
арифметичний простір
![]() є
векторним простором.
є
векторним простором.
3)
Сукупність
![]() всіх
матриць розмірності
всіх
матриць розмірності
![]() з дійсними елементами утворює дійсний
векторний простір відносно операцій
додавання матриць і множення матриць
на число.
з дійсними елементами утворює дійсний
векторний простір відносно операцій
додавання матриць і множення матриць
на число.
4) Множина
всіх геометричних векторів звичайного
тривимірного простору з початком в
точці
![]() відносно операцій додавання векторів
і множення векторів на число утворює
дійсний векторний простір
відносно операцій додавання векторів
і множення векторів на число утворює
дійсний векторний простір
![]() .
.
Множина
всіх векторів деякої площини і деякої
прямої відносно операцій додавання
векторів і множення векторів на число
також є дійсними векторними просторами.
Позначимо їх відповідно
![]() і
і
![]() .
.
5)
Сукупність всіх многочленів від змінної
![]() з дійсними коефіцієнтами відносно
операцій додавання многочленів і
множення многочленів на число утворює
дійсний векторний простір.
з дійсними коефіцієнтами відносно
операцій додавання многочленів і
множення многочленів на число утворює
дійсний векторний простір.
6)
Сукупність всіх неперервних функцій
дійсної змінної, які визначені на деякому
проміжку
![]() ,
утворює дійсний векторний простір
відносно операцій додавання функцій і
множення функцій на число. Роль
нуль-вектора відіграє функція, яка
тотожно дорівнює нулю.
,
утворює дійсний векторний простір
відносно операцій додавання функцій і
множення функцій на число. Роль
нуль-вектора відіграє функція, яка
тотожно дорівнює нулю.
З означення безпосередньо випливають наступні
Найпростіші властивості векторного простору:
1) Єдиність
нульового вектора. В
векторному просторі
![]() існує єдиний нульовий вектор, тобто
такий, що
існує єдиний нульовий вектор, тобто
такий, що
![]() :
:
![]() .
(аксіома 3)
.
(аксіома 3)
2) Єдиність
протилежного елемента. В
векторному просторі
![]() для будь-якого вектора
для будь-якого вектора
![]() існує
єдиний вектор
існує
єдиний вектор
![]() такий,
що
такий,
що
![]() .
(аксіома 4)
.
(аксіома 4)
3) Для будь-якого
вектора
![]()
![]() .
.
4) Для
будь-якого числа
![]() і
і
![]()
![]() .
.
5) Якщо
добуток
![]() ,
то або
,
то або
![]() ,
або
,
або
![]() .
.
6) Для
будь-якого вектора
![]() елемент
елемент
![]() є протилежним до
є протилежним до
![]() .
.
