29. Функциональные ряды. Основные понятия. Равномерная сходимость. Признак Вейерштрасса. Свойства равномерно сходящихся рядов. Понятие функционального ряда.

Пусть дана последовательность , z g. Выражение u_k(z)- называется функциональным рядом, заданным в g. Определение. Если при zg, соответствующий числовой ряд сходится к определенному комплексному числу w(z), то в g определена f(z)=w, которая называется суммой функционального ряда, а сам ряд называется сходящимся в g.

Если ряд сходится в g, то >0  N(,z): | r_n(z)| <для n N( ,z).

Необходимый и достаточный признак сходимости: Критерий Коши: для >0  N( ,z): | S_n+m(z)-S_n(z)| <для nN и m>0. Вообще говоря, в каждой точке zg N свое: N=N( ,z) и общего N для всей z может и не существовать.

Пусть задана последовательность функций , определенных на множестве .

Определение.   поточечно сходится к  на , если  , т.е. .

Определение. Последовательность  равномерно сходится к   при  на множестве , если . Это обозначается так:   на  при .

Равномерная сходимость функционального ряда – это равномерная сходимость последовательности его частичных сумм  к сумме ряда   на . Это равносильно тому, что  на  при , т.е. тому, что   на Теорема. (Критерий Коши равномерной сходимости последовательности ).  на множестве  .

Из этой теоремы сразу следует критерий Коши равномерной сходимости функционального ряда:   равномерно сходится на  .

Следствие. (Необходимый признак сходимости ряда). Положим в критерий Коши . Тогда получаем: , т.е. .

Теорема. (Признак Вейерштрасса). Пусть  выполняется неравенство . Пусть, кроме того, ряд   сходится. Тогда ряд  сходится на множестве   абсолютно и равномерно.

Доказательство. Достаточно проверить справедливость критерия Коши, т.е. доказать, что . Но последнее неравенство следует из того, что , а для ряда   выполняется критерий Коши, т.е. .

Свойства равномерно сходящихся функциональных рядов

1) Теорема о непрерывности суммы ряда.

1) Теорема о непрерывности суммы ряда.   Если члены ряда   - непрерывные на отрезке [a,b] функции и ряд сходится равномерно, то и его сумма S(x) есть непрерывная функция на отрезке [a,b].

 

  2) Теорема о почленном интегрировании ряда.   Равномерно сходящийся на отрезке [a,b] ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку [a,b] , сходится к интегралу от суммы ряда по этому отрезку.

  3) Теорема о почленном дифференцировании ряда.

  Если члены ряда   сходящегося на отрезке [a,b] представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.

30.Степенные ряды. Теорема Абеля.

Степенным рядом назовем ряд вида c_n(z-z₀)ⁿ, z₀ -центр, c _n - коэффициенты заданные комплексные числа. При z= z ₀ ряд сходится. Это может быть как единственная точка сходимости n!zⁿ , а также ряд может сходится на всей комплексной

плоскости zⁿ /n!. При исследовании степенного ряда важно установить область его равномерной сходимости. Как будет показано далее, область сходимости степенного ряда определяется видом его коэффициентов c _n.

1. Теорема Абеля. Теорема Абеля. Если степенной ряд c_n(z-z₀)ⁿ сходится в точке

z ₁ z₀ , то он сходится и при z: |z-z₀|<|z₁-z₀ |, причем в круге |z-z ₀| <|z₁-z₀| сходится равномерно. Доказательство. В силу необходимого условия сходимости ряда A>0 : для

n |c_n(z₁-z₀)ⁿ|<A =>|c_n|<A/|z₁-z₀|ⁿ =>|c_n(z-z₀)ⁿ|<A|(z-z₀)/(z₁-z₀)|ⁿ .

По условию теоремы |(z-z ₀)/(z₁-z₀)|=q<1=>|c_n(z-z₀)ⁿ|<Aqⁿ => ряд сходится.

При |z-z ₀| <|z₁-z₀ | ряд сходится равномерно по мажорантному признаку Вейерштрасса т.к. |c_n(z-z₀)ⁿ|A| /(z₁-z₀)|ⁿ < Aqⁿ , q<1 .

Следствия теоремы Абеля. 1.    Если степенной ряд расходится в точке z₂ z₀ , то он расходится и при z: |z-z₀|>|z₂-z₀ |. (Предполагая противное, получим, что по теореме Абеля ряд должен сходится в круге радиуса <|z-z₀ |, в частности и в точке z ₂ , что противоречит условию.). 2. Круг сходимости. Радиус сходимости. Рассмотрим s up|z₁-z₀ |=R для z₁ , где ряд сходится- точную верхнюю грань расстояний от точки z ₀ до точек z ₁ в которых сходится ряд c_n(z-z₀)ⁿ . Если R, то для z₂: |z₂-z₀ |>R ряд расходится. R=inf|z ₂-z₀ |=R для z₂ , где ряд расходится. ПустьR>0, тогда наибольшей областью сходимости степенного ряда является круг |z-z ₀|<R - круг сходимости степенного ряда, число R>0- радиус сходимости степенного ряда. Внутри круга сходимости ряд сходится, вне- расходится, в точках границы |z-z₀ |=R   может как сходиться, так и расходиться.

32 - Разложение функций в степянные ряды. теорема о единственности.

Если для любого отрезка при любомто

Доказательство. Для произвольного выберем H так, чтобы . Применим к формулу Тейлора с остаточным членом в форме Лагранжа: где По условию, и По признаку Даламбера ряд с членами сходится ().Поэтому его общий член стремится к 0, значит и при Ввиду произвольности получаем, что .

Для получения разложения заметим, что и для любого отрезка Поэтому лемма применима с , и мы получаем:

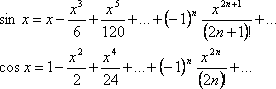
Теорема о единственности

Рассмотрим некоторое множество имеющее хотя бы одну предельную точку и функцию f(z), аналитическую в A и не равную тождественно постоянной. Далее, если существует большая область существует аналитическая в B функция w(z), тождественно совпадающая с f(z) на множестве A, то тождественное совпадение будет иметь место и на всем множестве B.

33. Формула Тейлора. Необходимое и достаточное условие разложимости функции в ряд Тейлора. Остаточный член формулы Тейлора в форме лагранжа.

Многочлен Тейлора:

Формула Тейлора:

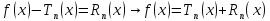
Для того чтобы функция была разложима в ряд Тейлора необходимо и достаточно, чтобы , при 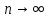. Док-во: в 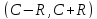разложима в ряд Тейлора

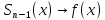, , (x) ,

Остаточный член формулы Тейлора в форме Лагранжа:

34. Достаточное условие разложимости функции в ряд Тейлора.

Если f(x) бесконечно дифференцируемая в (C-R;C+R) существует такое n существует х принадл этому промежутку (C-R;C+R), то функция f(x) в этом промежутке разложима в степенной ряд. Запишем остаточный член формулы Тейлора в форме Лангража

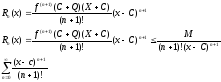
Сходится в каждой точке х принадл (-беск; + бескон)

35. Разложение e^x и a^x в ряд Макларена.

= c₀+c₁x+c₂x²+c₃x³+… - ряд Макларена

e^x=1+x+x²/2!+x³/3!+…

a^x=1+a²x²+a³x³+ a⁴x⁴+…

36, 37. Разложение и в ряд Макларена

38. Разложение в ряд Макларена

39. Разложение arctg x в ряд Макларена.

arctg x разлагается в ряд Макларена в интервале (-1, 1)

Биномиальный ряд, бесконечный ряд, являющийся обобщением формулы Ньютона бинома (1 + х) ⁿ на случай дробных и отрицательных показателей n: Биномиальный ряд сходится: при —1 < x <1, если n < —1; при —1< x £ 1, если —1 < n < 0; при —1 £ x £ 1, если n > 0.