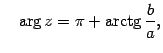- •6. Если всюду в области : то
- •Извлечение корня из комплексного числа
- •9) Однородные уравнения относительно отношения у/х. Уравнения, приводимые к однородным.
- •14. Линейные однородные уравнения второго порядка с постоянными коэффициентами (лемма1, лемма2).
- •27. Абсолютно и условно сходящиеся ряды и их свойства.
- •28. Признак Даламбера
- •29. Функциональные ряды. Основные понятия. Равномерная сходимость. Признак Вейерштрасса. Свойства равномерно сходящихся рядов. Понятие функционального ряда.
- •1) Теорема о непрерывности суммы ряда.
- •30.Степенные ряды. Теорема Абеля.

Определение двойного интеграла
Пусть
в замкнутой квадрируемой области
![]() плоскости
XOY задана функция
плоскости
XOY задана функция
![]() .
Разобьем область
.
Разобьем область
![]() произвольно
на n частей
произвольно
на n частей
![]() так
чтобы области
так
чтобы области
![]() не
имели общих внутренних точек. В каждой
замкнутой области
не
имели общих внутренних точек. В каждой
замкнутой области
![]() (внутри
или на границе) выберем произвольную
точку
(внутри
или на границе) выберем произвольную
точку
![]() и
умножим значение функции
и
умножим значение функции
![]() в
этой точке на площадь
в
этой точке на площадь
![]() .
Сложив все такие произведения, получим
сумму:
.
Сложив все такие произведения, получим
сумму:
![]() (1),
которая называется интегральной суммой
для функции
(1),
которая называется интегральной суммой
для функции
![]() в
области
в
области
![]() .
Интегральная сумма зависит от способа
разбиения области
.
Интегральная сумма зависит от способа
разбиения области
![]() на
части
на
части
![]() и
от выбора точек
и
от выбора точек ![]() на
этих частях, т.е. для функции
на
этих частях, т.е. для функции
![]() в
области
в
области
![]() можно
составить бесчисленное множество
интегральных сумм.
можно
составить бесчисленное множество
интегральных сумм.
Прежде чем переходить к операции предельного перехода, введем понятия диаметра области и шага разбиения области. Диаметром замкнутой области (двухмерного или трехмерного пространства) называется наибольшее из расстояний между двумя точками границы этой области. Шагом разбиения области на конечное число частей называется наибольший из диаметров областей деления.
Обозначим
через
![]() шаг
разбиения области
шаг
разбиения области
![]() на
части
на
части
![]() .
Процесс, состоящий в неограниченном
измельчении областей деления и
соответственно в неограниченном
увеличении числа n областей
деления, удобно характеризовать словами:
«шаг разбиения области
.
Процесс, состоящий в неограниченном
измельчении областей деления и
соответственно в неограниченном
увеличении числа n областей
деления, удобно характеризовать словами:
«шаг разбиения области
![]() стремится
к нулю».
стремится
к нулю».
Если
при стремлении к нулю шага разбиения
![]() области
области
![]() интегральные
суммы (1) имеют предел, то этот предел
называют двойным интегралом от функции
интегральные
суммы (1) имеют предел, то этот предел
называют двойным интегралом от функции
![]() по
области
по
области
![]() и
обозначают символами:
и
обозначают символами:
![]() или
или ![]() .
.
Здесь
![]() - подынтегральная функция,
- подынтегральная функция,
![]() - область интегрирования, x и y – переменные
интегрирования,
- область интегрирования, x и y – переменные
интегрирования,
![]() (dxdy)
- элемент площади. Таким образом, по
определению
(dxdy)
- элемент площади. Таким образом, по
определению
![]()
если этот предел существует.
Функция
![]() ,
для которой существует двойной интеграл
,
для которой существует двойной интеграл
![]()
называется
интегрируемой в области
![]() .
.
Свойства:
1.
Двойной интеграл
![]() не
зависит от обозначения переменных
интегрирования.
не
зависит от обозначения переменных
интегрирования.
2. Постоянный множитель k можно выносить за знак двойного интеграла:
![]()
3. Двойной интеграл от суммы двух функций равен сумме двойных интегралов от слагаемых:
![]()
4.
Если область
![]() разбита
на две области
разбита
на две области
![]() и
и
![]() ,
то
,
то
![]()
5.
Если всюду в области
![]() :
:
![]() то
то
![]()
6. Если всюду в области : то
7.
Если функция
![]() задана
в области
задана
в области
![]() ,
то
,
то
![]()
8.
![]()
Действительно,
так как в данном случае
![]() в
области
в
области
![]() ,
то для любого разбиения области
,
то для любого разбиения области
![]() на
части
на
части
![]() получим:
получим:
![]()
Свойство 8 позволяет использовать двойные интегралы для нахождения плоских фигур.
Вычисление двойных интегралов
Вычисление двойных интегралов сводится к вычислению определенных интегралов.
Теорема
1. Если функция
![]() непрерывна
в замкнутой области
непрерывна
в замкнутой области
![]() ,
ограниченной линиями x = a, y = b (a < b),
,
ограниченной линиями x = a, y = b (a < b),
![]()
![]()
![]() и
и
![]() -
непрерывные функции на отрезке [a,
b], причем
-
непрерывные функции на отрезке [a,
b], причем
![]() на
этом отрезке), то имеет место равенство
на
этом отрезке), то имеет место равенство
![]() (1)
(1)
позволяющее вычисление двойного интеграла свести к последовательному вычислению определенного интеграла от определенного интеграла (или, короче, к вычислению повторного интеграла).
Повторный интеграл, стоящий в правой части равенства (1), обычно записывают в виде:
![]()
Теорема
2. Если функция
![]() непрерывна
в замкнутой области
непрерывна
в замкнутой области
![]() ,
ограниченной линиями y = c, y = d (c<d),
,
ограниченной линиями y = c, y = d (c<d),
![]()
![]()
![]() и
и
![]() - непрерывные функции на отрезке [c,
d], причем всюду на этом
отрезке
- непрерывные функции на отрезке [c,
d], причем всюду на этом
отрезке
![]() (рис.3.8.1.)
то имеет место равенство
(рис.3.8.1.)
то имеет место равенство
![]() (2)
(2)
позволяющее сводить вычисление двойного интеграла к вычислению повторного интеграла.
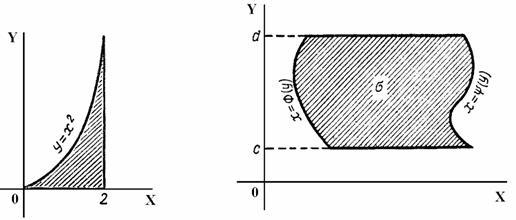
Рис. 3.8.1
При
вычислении двойного интеграла с помощью
повторного по формуле (2) сначала
вычисляется внутренний интеграл
 при
постоянном значении переменной y, в
пределах изменения x (для области
при
постоянном значении переменной y, в
пределах изменения x (для области
![]() )
при постоянном значении y,
)
при постоянном значении y,
![]() затем
полученная функция от y интегрируется
по y в максимальных пределах изменение
y для области
затем
полученная функция от y интегрируется
по y в максимальных пределах изменение
y для области
![]() .
.

Замена переменных в двойном интеграле
Якобиан
и его геометрический смысл. Пусть
даны две плоскости с выбранными на них
прямоугольными декартовыми системами
координат UOV и XOY.
Рассмотрим две (ограниченные или
неограниченные) области
![]() и
и
![]() ,
лежащие соответственно в плоскостях
UOV и XOY, и
предположим, что функции
,
лежащие соответственно в плоскостях
UOV и XOY, и
предположим, что функции
![]() (1)
(1)
устанавливают
взаимно однозначное соответствие между
точками этих областей. Это значит, что
каждой точке (u0, v0) области
![]() соответствует
одна определенная точка (x0,y0), где
соответствует
одна определенная точка (x0,y0), где
![]() области
области
![]() ,
называемая образом точки (u0, v0), и,
наоборот, каждой точке (x0,y0) области
,
называемая образом точки (u0, v0), и,
наоборот, каждой точке (x0,y0) области
![]() соответствует
одна определенная точка (u0, v0) области
соответствует
одна определенная точка (u0, v0) области
![]() [именно
та точка, образом которой является точка
(x0,y0)]. Будем говорить, что формулы (1)
задают взаимно однозначное отображение
области
[именно
та точка, образом которой является точка
(x0,y0)]. Будем говорить, что формулы (1)
задают взаимно однозначное отображение
области
![]() на
область
на
область
![]() (и
наоборот).
(и
наоборот).
Пусть
функции
![]() и
и
![]() непрерывны
в области
непрерывны
в области
![]() вместе
со своими частными производными первого
порядка. Тогда определитель
вместе
со своими частными производными первого
порядка. Тогда определитель
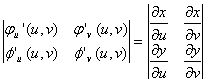
будет
непрерывной функцией переменных u и v,
определенной в области
![]() .
Этот функциональный определитель,
называемый определителем Якоби, или
якобианом отображения (1), принято
обозначать
.
Этот функциональный определитель,
называемый определителем Якоби, или
якобианом отображения (1), принято
обозначать
![]() или
символом
или
символом
![]() похожим
на символ, обозначающий производную.
похожим
на символ, обозначающий производную.
Вывод формулы замены переменных в двойном интеграле. Рассмотрим двойной интеграл
![]() (2)
(2)
от
функции
![]() ,
непрерывной в замкнутой области
,
непрерывной в замкнутой области
![]() ,
ограниченной кусочно-гладким контуром.
Предположим, что формулы
,
ограниченной кусочно-гладким контуром.
Предположим, что формулы
![]() (3)
(3)
задают
взаимно однозначное отображение
замкнутой области
![]() плоскости
UOV на замкнутую область
плоскости
UOV на замкнутую область
![]() плоскости
XOY, причем это отображение
удовлетворяет всем условиям, указанным
в начале параграфа.
плоскости
XOY, причем это отображение
удовлетворяет всем условиям, указанным
в начале параграфа.
![]()
Поставим
своей целью заменить двойной интеграл
(2) по переменным x и y
(по области
![]() )
равным ему двойным интегралом по
переменным u и v
(по области
)
равным ему двойным интегралом по
переменным u и v
(по области
![]() ).
Для этого разобьем область
).
Для этого разобьем область
![]() с
помощью кусочно-гладких кривых на n
областей
с
помощью кусочно-гладких кривых на n
областей
![]() Образы
этих кривых на плоскости XOY,
в свою очередь, будут кусочно-гладкими
кривыми. Они разобьют область
Образы
этих кривых на плоскости XOY,
в свою очередь, будут кусочно-гладкими
кривыми. Они разобьют область
![]() на
n областей
на
n областей
![]() Площади
соответствующих областей
Площади
соответствующих областей
![]() и
и
![]() связаны
соотношением
связаны
соотношением
где
![]() - некоторая точка в области
- некоторая точка в области
![]() ,
а
,
а
![]() -
якобиан отображения (3) в этой точке
(рис. 3.11.1.). Обозначим через
-
якобиан отображения (3) в этой точке
(рис. 3.11.1.). Обозначим через
![]() лежащий
в области
лежащий
в области
![]() образ
точки
образ
точки
![]() при
отображении (3):
при
отображении (3):
![]()
Для
полученного разбиения области
![]() на
части
на
части
![]() и
специального выбора точек
и
специального выбора точек
![]() на
этих частях составляем интегральную
сумму для двойного интеграла (3):
на
этих частях составляем интегральную
сумму для двойного интеграла (3):
![]()
По построению имеем:
![]() (4)
(4)

Рис. 3.11.1
В
правой части этого равенства стоит
интегральная сумма для двойного интеграла
по области
![]() от
непрерывной функции
от
непрерывной функции
![]() При
стремлении к нулю шага разбиения
При
стремлении к нулю шага разбиения
![]() области
области
![]() стремится
к нулю шаг разбиения
стремится
к нулю шаг разбиения
![]() области
области
![]() Переходя
к пределу в равенстве (3) получаем:
Переходя
к пределу в равенстве (3) получаем:
![]()
Эта формула и называется формулой замены переменных в двойном интеграле.
Двойной интеграл в полярных координатах
Пусть
в двойном интеграле
(1)
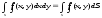
при обычных предположениях мы желаем перейти к полярным координатам r и f, полагая
x = r cos , y = r sin . (2)
Область интегрирования S разобьем на элементарные ячейки Si с помощью координатных линий r = ri (окружности) и = i (лучи)
Введем обозначения: rj = rj+1 - rj, i = i+1 - i
Так как окружность перпендикулярна (ортогональна) радиусам, то внутренние ячейки Si с точностью до бесконечно малых высшего порядка малости относительно их площади можно рассматривать как прямоугольники с измерениями rji и rj; поэтому площадь каждой такой ячейки будет равна:
Si = rj i rj (3)
Что касается ячеек Sij неправильной формы, примыкающих к границе Г области интегрирования S, то эти ячейки не повлияют на значение двойного интеграла и мы их будем игнорировать.
В качестве точки Mij Sij для простоты выберем вершину ячейки Sij с полярными координатами rj и i. Тогда декартовые координаты точки Mij равны:
xij = rj cos i, yij = rj sin i.
И следовательно,
f(xij,yij) = f(rj cos i, rj sin i) (3')
Двойной интеграл (1) представляет собой предел двумерной интегральной суммы, причем можно показать, что на значение этого предела не влияют добавки к слагаемым
интегральной
суммы, являющиеся бесконечно малыми
высшего порядка малости, поэтому учитывая
формулы (3) и (3'), получаем:
(4)
где d - максимальный диаметр ячеек Sij и сумма распространена на все ячейки указанного выше вида, целиком содержащиеся в области S. С другой стороны, величины i и rj суть числа и их можно рассматривать как прямоугольные декартовые координаты некоторых точек плоскости Or. Таким образом, сумма (4) является интегральной суммой для функции
f(r cos, r sin)r,
соответствующая прямоугольной сетке с линейными элементами i и ri. Следовательно
(5)

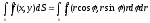
Сравнивая формулы (4) и (5), получим окончательно
(6)
Выражение
dS = r d dr
называется двумерным элементом площади в полярных координатах. Итак, чтобы в двойном интеграле (1) перейти к полярным координатам, достаточно координаты x и y заменить по формулам (2), а вместо элемента площади dS подставить выражение (7).
Для вычисления двойного интеграла (6) его нужно заменить повторным. Пусть область интегрирования S определяется неравенствами
Где r1(), r1() - однозначные непрерывные функции на отрезке [,].
Имеем
(8)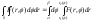
Где
F(r,) = rf(r cos, r sin)

Определение тройного интеграла и его свойства
Пусть
в замкнутой кубируемой области V
пространства XYZ задана
произвольная функция
![]() .
Разобьем область V на n
областей
.
Разобьем область V на n
областей
![]() не
имеющих общих внутренних точек. В каждой
точке области
не
имеющих общих внутренних точек. В каждой
точке области
![]() возьмем
произвольно точку
возьмем
произвольно точку
![]() .
Значение функции
.
Значение функции
![]() в
точке
в
точке
![]() умножим
на объем
умножим
на объем
![]() i-й
области и сложим такие произведения по
всем областям деления. Полученная сумма
i-й
области и сложим такие произведения по
всем областям деления. Полученная сумма
![]() называется
интегральной суммой для функции
называется
интегральной суммой для функции
![]() по
области V. Для функции
по
области V. Для функции
![]() можно
составить бесчисленное множество
интегральных сумм по области V.
можно
составить бесчисленное множество
интегральных сумм по области V.
Если
при стремлении к нулю шага разбиения
![]() области
V существует предел интегральных сумм,
то этот предел называется тройным
интегралом от функции
области
V существует предел интегральных сумм,
то этот предел называется тройным
интегралом от функции
![]() по области V и обозначается символами:
по области V и обозначается символами:
![]() или
или
![]()
При
этом
![]() -
подынтегральная функция, V – область
интегрирования, x, y и z – переменные
интегрирования,
-
подынтегральная функция, V – область
интегрирования, x, y и z – переменные
интегрирования, ![]() -
элемент объема.
-
элемент объема.
![]()
Таким образом, если этот предел существует.
Из определения следует, что тройной интеграл, так же как и двойной, не зависит от совершаемых при построении интегральных сумм разбиения области V на части и выбора точек на этих частях.
Тройные интегралы являются непосредственным обобщением двойных интегралов на случай трехмерного пространства.
Имеют место следующие достаточные условия существования тройного интеграла.
Теорема
1. Если функция
![]() непрерывна
в замкнутой области V, то тройной интеграл
непрерывна
в замкнутой области V, то тройной интеграл
![]() существует.
существует.
Решение задачи о массе области V с помощью тройного интеграла запишется в виде:
![]()
где
![]() - плотность распределения массы.
- плотность распределения массы.
В
этом и заключается механический смысл
тройного интеграла от неотрицательной
функции. Установить геометрический
смысл тройного интеграла
![]() для
произвольной функции
для
произвольной функции
![]() ,
не выходя за пределы трехмерного
пространства, не представляется
возможным. В случае, если в области V
,
не выходя за пределы трехмерного
пространства, не представляется
возможным. В случае, если в области V
![]() то
то
![]()
Таким образом, объем тела V можно вычислять с помощью тройного интеграла по формуле
![]()
Перечислим простейшие свойства тройных интегралов от функций, непрерывных в рассматриваемых областях.
1.
Тройной интеграл
![]() от
обозначения переменных интегрирования
не зависит, т.е.
от
обозначения переменных интегрирования
не зависит, т.е.
![]()
и т.д.
2. Постоянный множитель можно выносить за знак тройного интеграла:
![]()
где k – число.
3. Тройной интеграл от суммы двух функций равен сумме соответствующих интегралов от слагаемых:
![]()
4. Если область V разбита на две области V1 и V2, то
![]()
Примечание. Свойства 3 и 4 верны для любого фиксированного числа слагаемых.
5. Если в области V
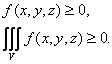
6.
Если в области V:
![]() то
то
![]()
7.
![]()
8.
Теорема о среднем. Если функция
![]() непрерывна
в замкнутой области V, то в этой области
существует точка
непрерывна
в замкнутой области V, то в этой области
существует точка
![]() ,
такая, что
,
такая, что
![]()
где V – объем данной области.
Замена
переменных в тройном интеграле
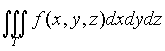 состоит
в переходе от переменных x, y, z к новым
переменным u, v, w по формулам
состоит
в переходе от переменных x, y, z к новым
переменным u, v, w по формулам
![]()
Если выполняются условия
1?. Отображение (6) взаимно однозначно;
2?.
Функции в (6) непрерывно - дифференцируемы
в области
![]()
3?. Якобиан отображения
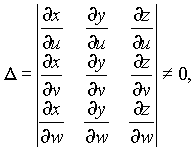
то имеет место формула
![]()
Формулы (6) называют криволинейными координатами (u, v, w) в области T. Рассмотрим примеры криволинейных координат.
Цилиндрические координаты представляют соединение полярных координат в плоскости xy с обычной декартовой аппликатой z (рис. 3).
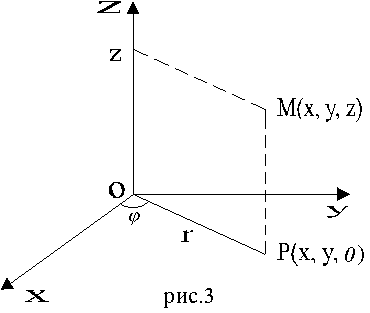
Пусть
M(x, y, z) - произвольная точка в
пространстве xyz, P - проекция
точки M на плоскость xy. Точка M
однозначно определяется тройкой чисел
![]() -
полярные координаты точки P, z -
аппликата точки M. Формулы, связывающие
их с декартовыми, имеют вид
-
полярные координаты точки P, z -
аппликата точки M. Формулы, связывающие
их с декартовыми, имеют вид
![]()
![]()
Якобиан
отображения (8)
![]()
Сферические
координаты. Пусть M(x,
y) - произвольная точка в пространстве
xyz, P - проекция точки M на
плоскость xy. Точка M однозначно
задаётся тройкой чисел
![]() ,
где r - расстояние точки M до точки
0,
,
где r - расстояние точки M до точки
0,
![]() -
угол между лучами OM и OZ,
-
угол между лучами OM и OZ,
![]() -
полярный угол точки P на плоскости
xy. Тройка чисел
-
полярный угол точки P на плоскости
xy. Тройка чисел
![]() называется
сферическими координатами точки M.
называется
сферическими координатами точки M.

Они связаны с прямоугольными формулами
![]()
![]()
Якобиан
отображения
![]() .
Иногда используются обобщённые
сферические координаты.
.
Иногда используются обобщённые
сферические координаты.
Объём V кубируемой области T (кубического тела) в пространстве xyz выражается формулой
![]()
Переходя в этом равенстве к новым переменным по формулам (6), получим выражение объёма области T в криволинейных координатах
![]()
Пусть
T - материальное тело (кубируемая
область) с плотностью
![]()
Тогда
![]() -
масса тела.
-
масса тела.
![]()
Криволинейные интегралы второго рода.
Пусть АВ – непрерывная
кривая в пространстве XYZ
(или на плоскости ХОY), а
точка P(x,
y, z) –
произвольная функция, определенная на
этой кривой. Разобьем кривую точками
![]() на
конечное число частичных дуг. И рассмотрим
сумму произведений значений функции в
каждой точке на длину соответствующей
частичной дуги.
на
конечное число частичных дуг. И рассмотрим
сумму произведений значений функции в
каждой точке на длину соответствующей
частичной дуги.
![]() ;
; ![]()
Определение. Если при стремлении к нулю шага разбиения кривой АВ интегральные суммы имеют конечный предел, то этот предел называется криволинейным интегралом по переменной х от функции P(x, y, z) по кривой АВ в направлении от А к В.
![]()
Криволинейный интеграл второго рода, т.е. интеграл по координатам отличается от криволинейного интеграла первого рода, т.е. по длине дуги тем, что значение функции при составлении интегральной суммы умножается не на длину частичной дуги, а на ее проекцию на соответствующюю ось. (В рассмотренном выше случае – на ось ОХ).
Вообще говоря, криволинейные интегралы могут считаться также и по переменным у и z.
![]()
![]()
Сумму криволинейных интегралов также называют криволинейным интегралом второго рода.
![]()
Свойства криволинейного интеграла второго рода.
1) Криволинейный интеграл при перемене направления кривой меняет знак.
![]()
2) ![]()
3)
![]()
4)
![]()
5) Криволинейный интеграл по замкнутой кривой L не зависит от выбора начальной точки, а зависит только от направления обхода кривой.
![]()
Направление обхода контура L задается дополнительно. Если L – замкнутая кривая без точек самопересечения, то направление обхода контура против часовой стрелки называется положительным.
6) Если АВ – кривая, лежащая в плоскости, перпендикулярной оси ОХ, то
![]()
Аналогичные соотношения справедливы при интегрировании по переменным у и z.
Теорема. Если кривая АВ – кусочно- гладкая, а функции P(x, y, z), Q(x, y, z) и
R(x, y, z) – непрерывны на кривой АВ, то криволинейные интегралы
![]()
![]() существуют.
существуют.
Вычисление криволинейных интегралов второго рода производится путем преобразования их к определенным интегралам по формулам:
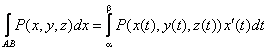
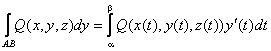

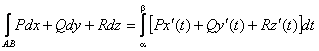
В случае, если АВ – плоская кривая, заданная уравнением y = f(x), то

Производная
функции комплексного переменного
определяется, как и производная в
действительной области:
![]() Здесь
z0,
Dz _
комплексные и Df(z0)
= f(z0+Dz)
- f(z).
Здесь
z0,
Dz _
комплексные и Df(z0)
= f(z0+Dz)
- f(z).
Используя это определение и свойства пределов, несложно убедиться в справедливости следующих правил дифференцирования.
1.
Сумма и произведение дифференцируемых
в точке функций, есть функция и
справедливы равенства:
![]()

2.
Частное дифференцируемых в точке
функций, при условии, что знаменатель
в точке не равен нулю, есть дифференцируемая
в этой точке функция, :
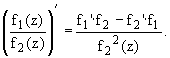
3. Сложная
функцияf(j
(z))
дифференцируема в точке z0,
если в этой точке дифференцируема
функция j
(z),
а функция f(u)
дифференцируема в точке u0,
где
u0
= j
(z0)
и u
= j
(z).
При этом в точке z0
имеет место формула:
![]()
Для элементарных функций комплексного переменного справедливы формулы дифференцирования, установленные для действительных значений аргумента.
Аналогично можно получить: (zn)' = nzn-1 (n - действительное число).
Если f(z) = f(x+iy) = u(x, y) + iv(x, y), т.е. u(x, y) = Re f(z) и v(x, y) = Im f(z), то справедливы следующие утверждения:
1. Если функция f(z) дифференцируема в точке, то в этой точке существуют частные производные ее действительной и мнимой частей u(x, y) = Re f(z), v(x, y) = Im f(z) и выполняется условие Коши-Римана:
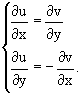
2. Если u(x, y) и v(x, y) дифференцируемы в точке (x0, y0) (имеют непрерывные частные производные в этой точке) и выполняется условие Коши-Римана, то функция f(z) = f(x+iy) = u(x, y) + iv(x, y) дифференцируема в точке z0 = x0+ iy0.
3. Производная дифференцируемой функции может быть записана по одной из формул:
![]()
![]()
![]()
![]()
Необходимое и дост. Условие дифиренйируемости: Даломбера-Эйлера, Каши-Римана
Чтобы ф-я f(z)=u(x,y)+iv(xy), определённая в G, была дифференцируемой в т. Z принадлежащей к G, необх. и дост. выполнение условий:
-
U и V – дифференцируемые как ф-ии двух переменных
-
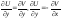

Модуль и аргумент.
Рассмотрим
на плоскости декартову прямоугольную
систему координат
![]() .
Каждому комплексному числу
.
Каждому комплексному числу
![]() можно
сопоставить точку с координатами
можно
сопоставить точку с координатами
![]() ,
и наоборот, каждой точке с координатами
,
и наоборот, каждой точке с координатами
![]() можно
сопоставить комплексное число
можно
сопоставить комплексное число
![]() .
Таким образом, между точками плоскости
и множеством комплексных чисел
устанавливается взаимно однозначное
соответствие. Поэтому комплекные числа
можно изображать как точки плоскости.
Плоскость, на которой изображают
комплексные числа, обычно называют
комплексной плоскостью.
.
Таким образом, между точками плоскости
и множеством комплексных чисел
устанавливается взаимно однозначное
соответствие. Поэтому комплекные числа
можно изображать как точки плоскости.
Плоскость, на которой изображают
комплексные числа, обычно называют
комплексной плоскостью.
Пример
17.3 Изобразим на
комплексной плоскости числа
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() :
:
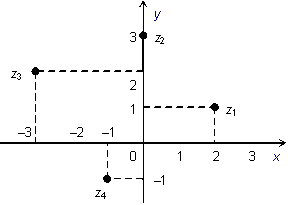
Рис.17.1.Изображение комплексных чисел точками плоскости
Однако чаще комплексные
числа изображают в виде вектора с началом
в точке
![]() ,
а именно, комплексное число
,
а именно, комплексное число
![]() изображается
радиус-вектором точки с координатами
изображается
радиус-вектором точки с координатами
![]() .
В этом случае изображение комплексных
чисел из предыдущего примера будет
таким:
.
В этом случае изображение комплексных
чисел из предыдущего примера будет
таким:
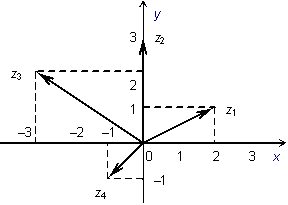
Рис.17.2.Изображение комплексных чисел векторами
Отметим, что изображением
суммы двух комплексных чисел
![]() ,
,
![]() является
вектор, равный сумме векторов, изображающих
числа
является
вектор, равный сумме векторов, изображающих
числа
![]() и
и
![]() .
Иными словами, при сложении комплексных
чисел складываются и векторы, их
изображающие (рис. 17.3).
.
Иными словами, при сложении комплексных
чисел складываются и векторы, их
изображающие (рис. 17.3).
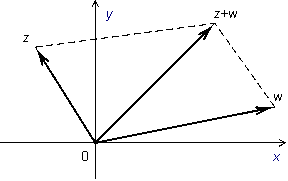
Рис.17.3.Изображение суммы комплексных чисел
Пусть комплексное число
![]() изображается
радиус-вектором. Тогда длина этого
вектора называется модулем числа
изображается
радиус-вектором. Тогда длина этого
вектора называется модулем числа
![]() и
обозначается
и
обозначается
![]() .
Из рисунка 17.4 очевидно, что
.
Из рисунка 17.4 очевидно, что
|
|
(17.6) |
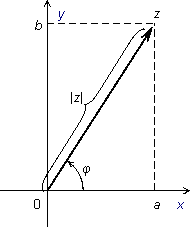
Рис.17.4.Модуль и аргумент
Угол, образованный
радиус-вектором числа
![]() с
осью
с
осью
![]() ,
называется аргументом числа
,
называется аргументом числа
![]() и
обозначается
и
обозначается
![]() .
Аргумент числа определяется не однозначно,
а с точностью до числа, кратного
.
Аргумент числа определяется не однозначно,
а с точностью до числа, кратного
![]() .
Однако, обычно аргумент указывают в
диапазоне от 0 до
.
Однако, обычно аргумент указывают в
диапазоне от 0 до
![]() или
в диапазоне от
или
в диапазоне от
![]() до
до
![]() .
Кроме того у числа
.
Кроме того у числа
![]() аргумент
не определен.
аргумент
не определен.
На рис. 17.4
![]() равен
углу
равен
углу
![]() .
Из того же рисунка очевидно, что
.
Из того же рисунка очевидно, что
![]()
С помощью этого соотношения можно находить аргумент комплексного числа:
|
|
(17.7) |
причем первая формула
действует, если изображение числа
![]() находится
в первой или четвертой четверти, а
вторая, если -- во второй или третьей.
Если
находится
в первой или четвертой четверти, а
вторая, если -- во второй или третьей.
Если
![]() ,
то комплексное число изображается
вектором на оси
,
то комплексное число изображается
вектором на оси
![]() и
его аргумент равен
и
его аргумент равен
![]() или
или
![]() .
.
Получим еще одну полезную
формулу. Пусть
![]() .
Тогда
.
Тогда
![]() ,
,
![]()
С учетом формулы (17.6)
получим
![]() или
или
![]()
Операции над комплексными числами
Пусть
![]() ,
,
![]() .
Найдем произведение
.
Найдем произведение
![]() :
:
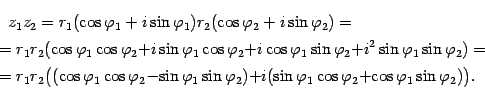
Заметим, что во внутренних скобках стоят формулы косинуса и синуса суммы аргументов. Поэтому
![]()
Последняя запись является
ригонометрической формой комплексного
числа
![]() .
Значит,
.
Значит,
![]()
![]()
иными словами, при умножении комплексных чисел их модули перемножаются, а аргументы складываются.
Аналогично можно доказать, что
![]()
иными словами, при делении комплексных чисел их модули делятся один на другой, а аргументы вычитаются.
Несложно проверить, что
если
![]() ,
то
,
то
![]()
Используя правило умножения
комплексных чисел в тригонометрической
форме, получим формулу для возведения
комплексного числа в степень
![]() ,
где
,
где
![]() --
натуральное число.
--
натуральное число.
Пусть
![]() .
Тогда
.
Тогда
![]()
то есть
![]()
Далее находим
![]()
то есть
![]()
Продолжая умножения дальше, придем к формуле
|
|
(17.9) |
Эта формула называется формулой Муавра.

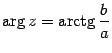 или
или