
- •6. Если всюду в области : то
- •Извлечение корня из комплексного числа
- •9) Однородные уравнения относительно отношения у/х. Уравнения, приводимые к однородным.
- •14. Линейные однородные уравнения второго порядка с постоянными коэффициентами (лемма1, лемма2).
- •27. Абсолютно и условно сходящиеся ряды и их свойства.
- •28. Признак Даламбера
- •29. Функциональные ряды. Основные понятия. Равномерная сходимость. Признак Вейерштрасса. Свойства равномерно сходящихся рядов. Понятие функционального ряда.
- •1) Теорема о непрерывности суммы ряда.
- •30.Степенные ряды. Теорема Абеля.
9) Однородные уравнения относительно отношения у/х. Уравнения, приводимые к однородным.
Опр.
Ф-ия F(x,y)
– называется однородной n-го
порядка, если выполняется равенство
![]()
![]() .
.
Опр.
Уравнение первого порядка ![]()
![]() ,
где ф-ия f(x,y)
является однородной несшего порядка
является однородным ДУ.
,
где ф-ия f(x,y)
является однородной несшего порядка
является однородным ДУ.
Уравнения
приводимые к однородным ![]()
![]() где правая часть представляет собой
непрерывную ф-ию 2-го случая.
где правая часть представляет собой
непрерывную ф-ию 2-го случая.
1
случай ![]()
![]() уже однородное
уже однородное
2
случай ![]()
![]() или один из них. Данное уравнение будет
приводимо к уравнению с разделяющимися
переменными или к однородному.
или один из них. Данное уравнение будет
приводимо к уравнению с разделяющимися
переменными или к однородному.
-
Если имеет место следующее:
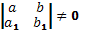
 далее
делаем замену
далее
делаем замену 
 где (l,m) это
решение системы
где (l,m) это
решение системы 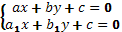
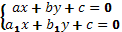 при етом dx=d(
при етом dx=d(
 )=
)=

-
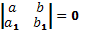
 в этом случае делаем подстановку
z=ax+by
=>
в этом случае делаем подстановку
z=ax+by
=> 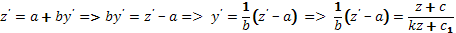


-
. В результате получаем уравнение с разд. Переменными. Когда найдем общее решение этого уравнения нужно будет вернуться к старой переменной.
![]() Дифференциальные
уравнения высших порядков Дифференциальные
уравнения порядка выше первого называются
дифференциальными уравнениями высших
порядков. В основном ограничимся
уравнениями второго порядка.
Дифференциальным уравнением второго
порядка называется уравнение вида
F(x,y,y,y)=0 (1). Решением уравнения (1) называется
функция y=ϕ(x),
которая при подстановке в уравнение
обращает его в тождество. Общим решением
уравнения (1) называется функция y = ϕ(x,
C1 , C2 ), которая является решением (1) и
любое решение может быть получено из
нее при некоторых C1 и C2 . Начальными
условиями для решения y = ϕ(x)
уравнения (1) называется тройка чисел
x0 , y0 , y0 такая, что y |x=x0 =y0 , y |x=x0 = y0 . Задача
нахождения решения, удовлетворяющего
данным начальным условиям, называется
задачей Коши. Для нее имеет место теорема
существования и единственности,
аналогичная той, которая рассматривалась
для дифференциальных уравнений первого
порядка. В некоторых случаях уравнение
второго порядка можно привести к
уравнениям первого порядка. Рассмотрим
такие случаи.
Дифференциальные
уравнения высших порядков Дифференциальные
уравнения порядка выше первого называются
дифференциальными уравнениями высших
порядков. В основном ограничимся
уравнениями второго порядка.
Дифференциальным уравнением второго
порядка называется уравнение вида
F(x,y,y,y)=0 (1). Решением уравнения (1) называется
функция y=ϕ(x),
которая при подстановке в уравнение
обращает его в тождество. Общим решением
уравнения (1) называется функция y = ϕ(x,
C1 , C2 ), которая является решением (1) и
любое решение может быть получено из
нее при некоторых C1 и C2 . Начальными
условиями для решения y = ϕ(x)
уравнения (1) называется тройка чисел
x0 , y0 , y0 такая, что y |x=x0 =y0 , y |x=x0 = y0 . Задача
нахождения решения, удовлетворяющего
данным начальным условиям, называется
задачей Коши. Для нее имеет место теорема
существования и единственности,
аналогичная той, которая рассматривалась
для дифференциальных уравнений первого
порядка. В некоторых случаях уравнение
второго порядка можно привести к
уравнениям первого порядка. Рассмотрим
такие случаи.
Уравнение, не содержащее в явном виде искомой функции и ее первой производной. Уравнение не содержит в явном виде искомой функции и ее первой производной. Оно может быть записано в виде y = f (x). Очевидно y = (y ) = f (x), откуда y = f (x) dx + C1 и y=f(x)dx+C1 dx+C2=f (x) dx dx+C1 x+C2 (здесь интеграл подразумевает какую-либо первообразную).
Замечание 1 Так же можно решать уравнения любого порядка, имеющие вид y (n) = f (x). Пример 1 Решить уравнение y = cos x. Решение y = cos x dx + C1 = sin x + C1 , y=(sin x+C1)dx+C2 . Общее решение y = − cos x + C1 x + C2 (здесь интегралы означают первообразные !).
Уравнение, не содержащее в явном виде искомой функции
Уравнение не содержит в явном виде искомой функции, т.е. имеет вид F (x, y , y ) = 0. (2) Понизить его порядок можно введением новой неизвестной
функции y = p(x)=p. Тогда y=p, и уравнение примет вид F(x,p,p)=0. Его общее решение p=p(x,C1) или y=p(x,C1). Общее решение уравнения (2): y=p(x,C1) dx+C2. Пример 2 Решить уравнение xy =y. Решение Введем неизвестную функцию y =p, y=p . Уравнение dp dx примет вид xp=p; ln|p|=ln |x|+ln |C|; p=Cx; px
C y=Cx; y=x2+C2=C1 x2+C2. Общее решение y=C1x+C2.

Определение.
Линейным дифференциальным уравнением
n – го порядка
называется любое уравнение первой
степени относительно функции у и
ее производных
![]() вида:
вида:
![]()
где p0, p1, …,pn – функции от х или постоянные величины, причем p0 0.
Левую часть этого уравнения обозначим L(y).
![]()
Определение. Если f(x) = 0, то уравнение L(y) = 0 называется линейным однородным уравнением, если f(x) 0, то уравнение L(y) = f(x) называется линейным неоднородным уравнением, если все коэффициенты p0, p1, p2, … pn – постоянные числа, то уравнение L(y) = f(x) называется линейным дифференциальным уравнением высшего порядка с постоянными коэффициентами.
Определение. Фундаментальной системой решений линейного однородного дифференциального уравнения n –го порядка на интервале (a, b) называется всякая система n линейно независимых на этом интервале решений уравнения.
Определение. Если из функций yi составить определитель n – го порядка
 ,
,
то этот определитель называется определителем Вронского.
Теорема. Если
функции
![]() линейно
зависимы, то составленный для них
определитель Вронского равен нулю.
линейно
зависимы, то составленный для них
определитель Вронского равен нулю.
Теорема. Если
функции
![]() линейно
независимы, то составленный для них
определитель Вронского не равен нулю
ни в одной точке рассматриваемого
интервала.
линейно
независимы, то составленный для них
определитель Вронского не равен нулю
ни в одной точке рассматриваемого
интервала.
Теорема. Для
того, чтобы система решений линейного
однородного дифференциального уравнения
![]() была фундаментальной необходимо и
достаточно, чтобы составленный для них
определитель Вронского был не равен
нулю.
была фундаментальной необходимо и
достаточно, чтобы составленный для них
определитель Вронского был не равен
нулю.
Теорема. Если
![]() - фундаментальная система решений на
интервале (a, b),
то общее решение линейного однородного
дифференциального уравнения является
линейной комбинацией этих решений.
- фундаментальная система решений на
интервале (a, b),
то общее решение линейного однородного
дифференциального уравнения является
линейной комбинацией этих решений.
![]() ,
где Ci
–постоянные коэффициенты.
,
где Ci
–постоянные коэффициенты.
