14. Линейные однородные уравнения второго порядка с постоянными коэффициентами (лемма1, лемма2).

(1), где p, q – некоторые константы

Опр: Ур-е называется характеристическим уравнением

Лемма1: Если корень хар-го ур-я, то решение ур-я.

Лемма2: Если комплексная функция вида явл-ся реш-ем (1)-го ура-я, то ф-ии и также явл-ся реш-ем этого ур-я.

1) составляют соответствующее ему характеристическое уравнение (заменяя в однородном уравнении производные от искомой функции на k в соответствующей степени, то есть  на ,  на  и  на )

                                                        (18).

Полученное квадратное уравнение может иметь (в зависимости от дискриминанта ) два различных действительных решения, два совпадающих (кратный корень) действительных решения и пару комплексно-сопряженных решений;

2) в зависимости от корней характеристического уравнения выделяются частные решения (соответствующие корням характеристического уравнения), образующие фундаментальную систему решений и записывается соответствующее общее решение (18).

	Корни характеристического уравнения	Частные решения	Общее решение однородного дифференциального уравнения
I	Два действительных и различных корня, т.е. ,
II	Два действительных и совпадающих корня, т.е.
III	Два комплексно сопряженных решения, т.е.

18 - Тригонометрическая форма записи комплексного числа.Формула (тут что-то непонятное) Муавра. Радикал. Степень с рациональным показателем.

Пусть и φ = arg z. Тогда по определению аргумента имеем:

Отсюда получается z = a + bi = r(cos φ + i sin φ).

Такая форма называется тригонометрической формой записи комплексного числа.

Муавра формула

формула, содержащая правило для возведения в степень n комплексного числа, представленного в тригонометрической форме

z = ρ (cos φ + i sin φ);

согласно М. ф., модуль ρ комплексного числа возводится в эту степень, а аргумент φ умножается на показатель степени

zn = [ρ (cos φ + i sin φ)] n = ρn (cos nφ + i sin nφ).

Степень с рациональным показателем

a1 = a − определение степени с натуральным показателем

определение степени с положительным дробным показателем.

.

a0 = 1, a ≠ 0 − определение степени с нулевым показателем.

определение степени с отрицательным дробным показателем.

Пусть a, b > 0 − любые рациональные числа. Тогда степень с любым рациональным показателем обладает следующими свойствами.

ar · as = ar + s

ar : as = ar – s

(ar)s = ars

ar · br = (ab)r

Метод неопределённых коэффициентов, или как его ещё можно назвать, метод подбора по правой части. Функции, стоящие в правой части, для которых может быть использован данный метод, это – многочлены, синусы, косинусы, экспоненты, а также различные их комбинации. В связи с этим, запишем f(t) в следующем общем виде:

Основная идея метода подбора решения уравнения по правой части (2.4) заключается в том, что частное решение этого уравнения ищется в виде функции такого же вида

только новые коэффициенты многочленов g0,g1,…,gn и h1,h2,…,hn в начале считаются неопределёнными. Кроме того, степени обоих этих многочленов теперь считаются равными наибольшей степени (пусть n>m). Значение числа k определяется с помощью следующего правила. Пусть - дискриминант характеристического уравнения, соответствующего однородному уравнению

Тогда:

1. Если D=0 и l - корень характеристического уравнения, а , то k=2.

2. Если D>0 и l - корень характеристического уравнения, а , то k=1

3. Если D<0 и , а , то k=1.

4. Во всех остальных случаях k=0.

Коэффициенты многочленов g0,g1,…,gn и h1,h2,…,hn определяются при подстановке в исходное уравнение с правой частью. Если правая часть неоднородного уравнения представляет собой комбинацию функций вида, то есть f(t)=f1(t)+f2(t): то частным решением такого уравнения будет являться сумма частных решений уравнений

Определение:

Сумма ряда, или бесконе́чная су́мма, или ряд, — математическое выражение, позволяющее записать бесконечное количество слагаемых и подразумевающее значение их суммы, которое можно получить в предельном смысле. Если значение суммы (в предельном смысле) существует, то говорят, что ряд сходится. В противном случае говорят, что он расходится.

Пусть — последовательность чисел. Число называется n-ой частичной суммой ряда .

Сумма (числового) ряда — это предел частичных сумм S_n, если он существует и конечен. Таким образом, если существует число , то в этом случае пишут .

Геометрическая прогрессия:

последовательность чисел (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число q (знаменатель прогрессии), где и обычно предполагают ещё что

Формула общего члена такова

b_n = b₁q^{n − 1}.

Свойства геометрической прогрессии:

• Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.

• 

• Если b₁ > 0 и q > 1, прогрессия является возрастающей, если 0 < q < 1, — убывающей, а при q < 0 — знакопеременной

Сходимость:

Если ряд сходится то общий член ряда стремится к нулю.

Признак Д'Аламбера:

Если для числового ряда существует такое число q, 0 < q < 1, что начиная с некоторого номера выполняется неравенство то данный ряд абсолютно сходится; если же, начиная с некоторого номера то ряд расходится.

Радикальный признак Коши: Если для числового ряда с неотрицательными членами существует такое число d, 0 < d < 1, что, начиная с некоторого номера, выполняется неравенство то данный ряд сходится.

Интегральный признак Коши:

Пусть для функции f(x) выполняется:

1. (функция принимает только положительные значения)

2. (функция монотонно убывает)

3. f(n) = a_n

Тогда ряд и несобственный интеграл сходятся или расходятся одновременно.

Для сходящихся рядов c комплексными членами справедливы все свойства рядов с действительными членами:         Необходимый признак сходимости ряда. Общий член сходящегося ряда стремится к нулю при n → ∞.         Если сходится ряд , то сходится любой его остаток, Обратно, если сходится какой-нибудь остаток ряда, то сходится и сам ряд.         Если ряд сходится, то сумма его остатка после n-го члена стремится к нулю при n → ∞.         Если все члены сходящегося ряда умножить на одно и то же число с, то сходимость ряда сохранится, а сумма умножится на с.         Сходящиеся ряды (А) и (В) можно почленно складывать и вычитать; полученный ряд тоже будет сходиться, и его сумма равна S_A ± S_B .         Если члены сходящегося ряда сгруппировать произвольным образом и составить новый ряд из сумм членов в каждой паре круглых скобок, то этот новый ряд тоже будет сходиться, и его сумма будет равна сумме исходного ряда.         Если ряд сходится абсолютно, то при любой перестановке его членов сходимость сохраняется и сумма не изменяется.         Если ряды (А) и (В) сходятся абсолютно к своим суммам S_А и S_B, то их произведение при произвольном порядке членов тоже сходится абсолютно, и его сумма равна S_А·S_А.

Положительный ряд, это ряд без отрицательных членов. Критерий сходимости:

Т: Для того, что бы положительный сходился, необходимо и достаточно, что бы последовательность его частичных сумм была ограничена сверху числом

Необходимость: Дано ряд - положительный, сходящийся

Доказать: |S_n|<M, при любом n

Пусть , по теореме об ограниченности сходящихся последовательностях => что |S_n|<=M , функция ограничена сверху

Признак сравнения

Если то из сходимости ряда следует сходимость ряда , а из расходимости ряда , а из расходимости ряда - расходимость ряда

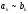Если то при 0 < l < ряды и или оба сходятся, или оба расходятся; при l=0 из сходимости ряда следует сходимость ряда ; при l= из расходимости ряда следует расходимость ряда . В частности, если при ,то ряды и или оба сходятся, или оба расходятся.

1)Признак Деламбера для степенных, показательных и содержащих факториалы рядов: Если k < 1 то ряд сходится, если k > 1 то расходится.

2)Признак Коши для выражений в степени n: Если k < 1 то ряд сходится, если k > 1 то расходится

Если функция f (x) на промежутке [1; +oo) является непрерывной, положи­тельной и невозрастающей, то числовой ряд

сходится или расходится одновременно с интегралом

В математике, гармонический ряд представляет собой сумму бесконечного количества членов обратных последовательным числам натурального ряда. Вычисление

n-нной частичной суммой s_n гармонического ряда называется n-нное гармоническое число:

Сходимость ряда  при 

Теоретико числовые свойства частичных сумм

В знакочередующемся ряде любые соседние члены имеют противоположные знаки.

Т Лейбнца: ряд а₁-а₂+а₃-а₄+…+а_n(-1)ⁿ⁺¹+…. = . Если члены знакочередующегося ряда монотонно убывая по величине стремятся к 0, то ряд сходится.

Доказательство: Запишем чётные частные суммы S_2m=(a₁-a₂)+(a₃-a₄)+…+(a_2m-1-a_2m) => {S_am} монотонно возрастает. S_2m< S_2m+2 S_2m<a₁.

По теореме о пределе монотонной последовательности пусть .

S_2m+1= а₁-а₂+а₃-…+a_2m-1-a_2m+a_2m+1-… S_2m+1=S_2m+a_2m+1. S_2m стремится к S, a_2m+1 стремится к 0.

Следствие: Абсолютная величина остатка ряда лебнцевского типа не превосходит абсолютной величины первого члена. |R_n|<=a_n+1.

S_2m<S< S_2m+1 S-S_2m<= S_2m+1 - S_2m S_2m+1-S<= S_2m+1- S_2m