27. Абсолютно и условно сходящиеся ряды и их свойства.

Знакопеременные ряды (абсолютно и условно сходящиеся).

(1), (2)

Опр.: Если сходится ряд (2), то ряд (1) –абсолютно сх-ся. Если сх-ся (1), а (2) – расх-ся, то ряд (1) условно сх-ся.

Св-ва:

1)Сумма абсолютно сх-ся ряда равна разности сумм 2-х полож-ых рядов, состав-ых из полож-х членов и абсол-ых величин всех его отриц-ых членов.

2)Абсолютно сх-ся ряды обладают переместительным свойством

3)Абсолютно сх-ся ряды можно перемножать

4)Для абсолютно сх-ся рядов справедливо нер-во, что

Условно сх-ся ряды этим св-ом не обладают.

Теорема Римана: Условно сх-ся ряды не обладают переместительным св-ом, т.е. если ряд сх-ся условно, то можно указать такую перестановку его членов, что сумма ряда будет любым наперед заданным числом. Ряд может быть расходящимся.

28. Признак Даламбера

  Пусть дан ряд u₁+u₂+u₃+...+u_n+... , (1)с положительными членами.   Относительно этого ряда имеют место две следующие теоремы Даламбера.

  Теорема 1. Если отношение каждого последующего члена ряда (1) к предидущему члену меньше фиксированного числа q<1 (или равно q), то ряд (1) сходится; если это отношение больше 1 (или равно 1), то ряд (1) расходится.   Доказательство. 1. Пусть

  Тогда имеют место неравенства (2)

Отсюда (3)

или (4)

Складывая почленно неравенства (4), получим неравенство

(5)

Но

а поэтому

По условию теоремы, q<1 , а поэтому

Следовательно, при любом n.

Прибавляя u₁ к обеим частям последнего неравенства, получим

Или .   Так как все члены ряда (1) положительны и, следовательно, S_n с возрастанием n возрастает, оставаясь меньше то существует предел S_n и

  Таким образом ряд (1) сходится.   2. Теперь пусть

Это означает, что с возрастанием n общий член u_n ряда (1) не убывает, т.е. не выполняется необходимый признак сходимости ряда, а поэтому ряд (1) расходится.

Теорема 2. Пусть l - предел отношения последующего члена u_n+1 ряда (1) к предыдущему u_n при n , т.е.

Тогда,   если l < 1, то ряд l сходится,   если l > 1, то ряд l расходится,   Если же l = 1, то вопрос о сходимости ряда (1) остается открытым.   Доказательство. Согласно определению предела переменной величины, равенство

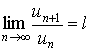
означает, что, начиная с некоторого номера n, выполняются неравенства

где e   - наперед заданное сколь угодно малое положительное число.  Рассмотрим три случая:  а) пусть l < 1 . Тогда всегда можно взять e   настолько малым, чтобы выполнялось неравенство

l +   < 1

и, начиная с некоторого n , неравенство

где q = l + , в силу чего (см. теорему 1) ряд (1) будет сходящимся;

б) пусть l > 1 . Выбираем e   так, чтобы

 = l - 1 > 0

  Тогда l -  = 1 и

т.е. ряд (1) расходится (см. теорему 1) в) пусть l = 1 . Тогда ряд (1) может быть как сходящимся, так и расходящимся.