-
Показатели вариации.
7.1. Колеблемость и вариация как измеритель колеблемости.
Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае.
Колеблемость отдельных значений характеризуют показатели вариации. Термин «вариация» произошел от лат. variatio — изменение, колеблемость, различие. Однако не все различия принято называть вариацией.
Под вариацией в статистике понимают такие количественные изменения величины изучаемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают случайную и систематическую вариации. Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов. Например, можно оценить, насколько однородной является совокупность. Для характеристики совокупностей и исчисленных средних величин важно знать, какая вариация изучаемого признака скрывается за средними.
Основа показателей — общая оценка отклонений значений показателей элементов совокупности от средней.
Размах представляет собой разность между максимальной и минимальной величиной признака и является простейшей характеристикой вариации:
.
(7.1)
Среднее
линейное отклонение
:
,
(7.2)
где X — значение показателя;
—
среднее
арифметическое значение.
Среднее линейное отклонение в чистом виде для анализа не применяют. Оно ввиду использования модуля не очень удобно для расчетов, что и объясняет малую употребительность данной характеристики вариации.
7.2. Дисперсия и стандартное отклонение.
Сумма квадратов отклонений от среднего является основой для вычисления относительного показателя — дисперсии в простейшем случае несгруппированных данных:
, (7.3)
или дисперсия для сгруппированных данных и для интервальных рядов:
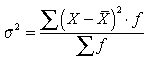, (7.4)
где
.
Корень квадратный из дисперсии называется средним квадратическим отклонением, или стандартным отклонением, и обозначается σ .
В отличие от дисперсии, этот показатель, также показывающий степень вариации признака, имеет размерность самого признака, а не его квадрата, что представляет определенное удобство. Далее мы увидим, что стандартное отклонение имеет важное значение в теории оценивания неизвестных параметров (например, среднего генеральной совокупности) и в теории ошибок выборочного наблюдения.
Еще одним важным показателем, характеризующим вариацию признака и позволяющим сравнивать вариации различных совокупностей, является коэффициент вариации:
. 
(7.5)
По величине коэффициента вариации можно судить о степени вариации признаков совокупностей. Чем больше его величина, тем больше разброс значений вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%. Коэффициент вариации важен и в тех случаях, когда нужно сравнивать средние квадратические отклонения, выраженные изначально в разных единицах измерении, для различных совокупностей.
Дисперсия характеризуется двумя важными и весьма полезными для ее вычисления свойствами:
1) если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия от этого не изменится;
2) Если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия соответственно уменьшится или увеличится в i2 .