2.2.6. Алгоритм расчета неизобарического участка струи

1. Исходными данными являются параметры на срезе сопла "а":

; ; ; ; .

2. Определяем дополнительные параметры и критерии для среза сопла:

;

; ;

; ,

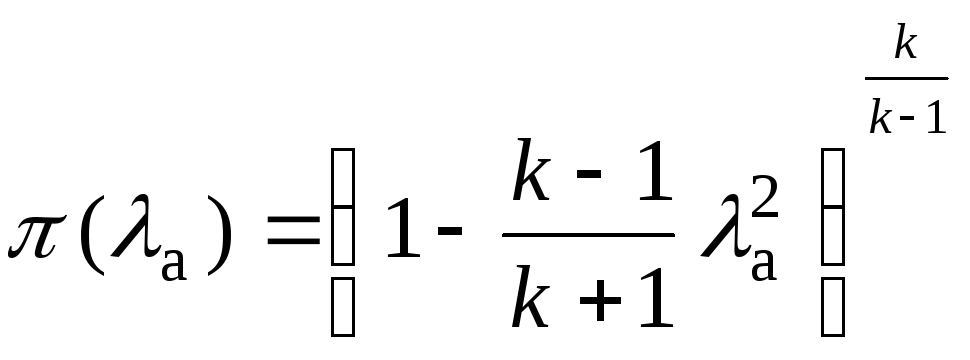и – постоянные для всех сечений;

;

; ;

;

;

; ;

.

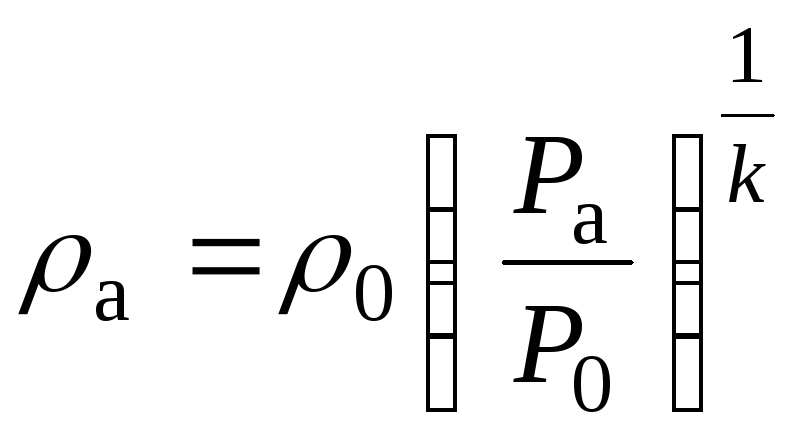3. Определяем длину структуры по сечениям и суммарную длину начального участка .

Сечения 1', 2', 3' и 4' откладываем по середине сечений 1–2, 2–3 и т.д.

4. Определяем параметры конечного неизобарического сечения по условию . Тогда ; ; и т.д.

5. Строим графическую зависимость в диапазоне

,

две точки которой уже определены координатами: и . Значения могут быть заданы для всех сечений путем деления диапазона на пять частей

.

Тогда , , то есть , . Под значения могут быть подобраны при помощи компьютера определенные значения . Однако для графического решения целесообразно задаться несколькими фиксированными значениями , например из условия

,

и для этих значений определить . Таким образом можно построить параболу (см. рис.2.16).

6. По построенному графику можно определить точные значения в сечениях и т.д. по значениям , определенным в предыдущем пункте:

.

Ход изменения в сечениях можно представить на графике (см. рис.2.16). От сечения "а" до сечения 1 течение проходит с ударно-волновыми потерями давления (сужение потока). От сечения 1 до сечения 1' течение проходит изоэнтропически, без потерь (расширение потока). Далее циклически повторяется сужение и расширение потока до сечения "к", после которого течение становится изобарическим.

7. По имеющимся в каждом сечении струи по формулам (2.1)–(2.5) определяются все параметры течения. Параметры сводятся в таблицу и представляются графически функцией .

8. При расчете параметров струи с возникают трудности из-за малых отличий параметров сечений от параметров на срезе сопла и в сечениях. В то же время реальная струя, в силу неравномерности в распределении параметров на срезе, будет иметь достаточно ярко выраженную волновую структуру. Поэтому рекомендуется проводить расчеты по данной методике, определяя параметры в расчетных сечениях для условий , а затем проводить пересчет на условие .

Это возможно на основе следующего свойства газодинамического участка струи. Экспериментально получено, что при имеет место универсальная зависимость в широких пределах изменения : . Диапазон изменения . Тогда возможно применение следующей формулы пересчета параметров струи при на параметры струи при :

.

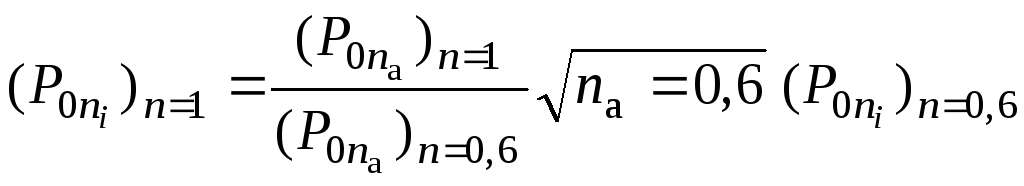Изложенные методика и алгоритм расчета позволяют качественно объяснить особенности неизобарического участка струи. Для большего соответствия экспериментальным данным методика расчета может быть уточнена следующим образом.

В минимальных сечениях "бочек" (нечетные номера) местные значения и на оси реальных струй и осредненные по сечению, согласно предлагаемой методике, близки между собой. Параметры, полученные в расчете, превышают экспериментальные не более чем на . Однако осредненные параметры в максимальных сечениях "бочек" могут более существенно отличаться от действительных значений на оси из-за большей неравномерности потока в максимальных сечениях, чем в минимальных.

В целях лучшего соответствия с экспериментальными данными местная скорость на оси в точке первого минимума давления рекомендуется определять по формуле

,

где расстояние до точки пересечения (отражения) скачков на оси

.

После этого по величине по формуле

вычисляется первый минимум давления на оси струи. Этим достигается учет доразгона потока после среза сопла, имеющий место в реальных течениях.

Величину последующих минимумов давления на оси можно вычислить по зависимости:

,

где – величина первого минимума давления на оси; – расстояние от среза сопла до второго минимума давления; – расстояние от среза сопла до определяемого минимума давления.

Далее по определяют .

Геометрия струи определяется следующими зависимостями:

• расстояние до пересечения скачков

;

• длина начального участка струи ;

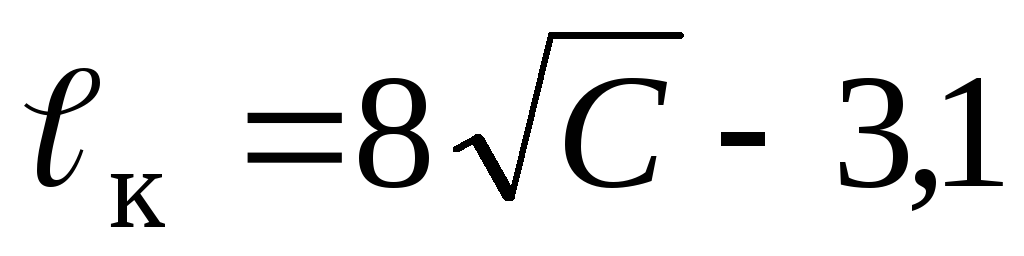• длина структуры ;

• расстояние до максимального диаметра "бочки"

; ;

• длину сужающегося участка можно принять примерно за ;

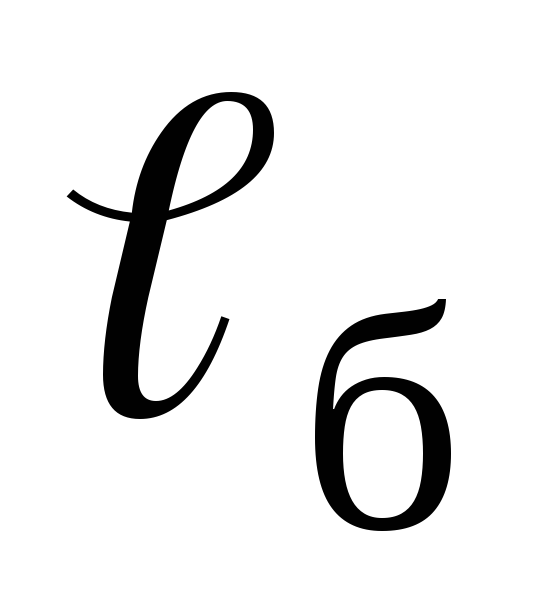• максимальный диаметр первой "бочки"

.

Пример расчета струи.

Исходные параметры: ; ; ; .

1. Из таблиц газодинамических функций находим ; ; .

2. По формулам и определяем ; ; ; .

3. По диаграмме устанавливаем, что реализуется режим х-образных скачков.

4. Определяем геометрию струи:

• расстояние до пересечения скачков

;

• длина начального участка струи ;

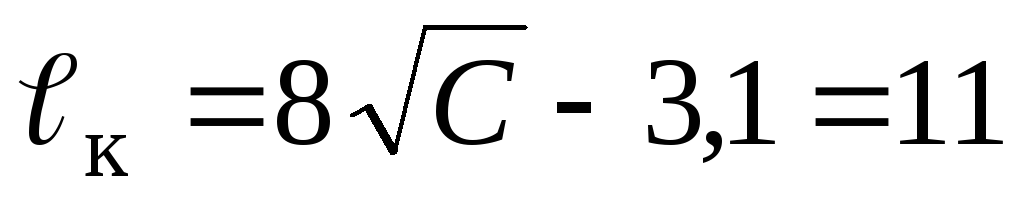• длина структуры ;

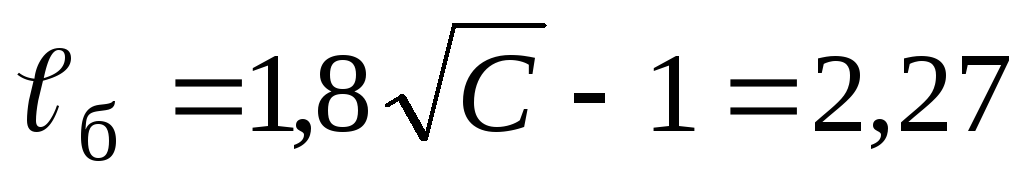• расстояние до максимального диаметра "бочки"

;

• число "бочек" .

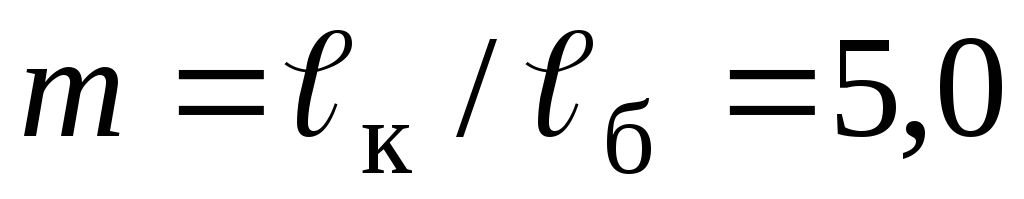5. Строим графики .

Величина потерь в пределах одной "бочки"

.

По построенным графикам находим и для характерных сечений. В минимальных сечениях "бочки" параметры равны осредненным.

6. Определяем местные значения в точке пересечения скачков на оси:

; .

Из графика (см. рис.2.16) определяем .

Последующие минимумы давления на расстояниях ; ; ; определяем по формуле

.

Величина для второго, третьего, четвертого и пятого минимумов будет 1; 2; 3 и 4 соответственно. Тогда будут ; ; и .