Учитывая, что , получим

.

Из исходной системы уравнений могут быть получены формулы, связывающие параметры течения после скачка , или ,, и с исходными параметрами до скачка , или ,, и .

Параметры и будут связаны с и уравнением ударной адиабаты (адиабата Гюгонио)

,

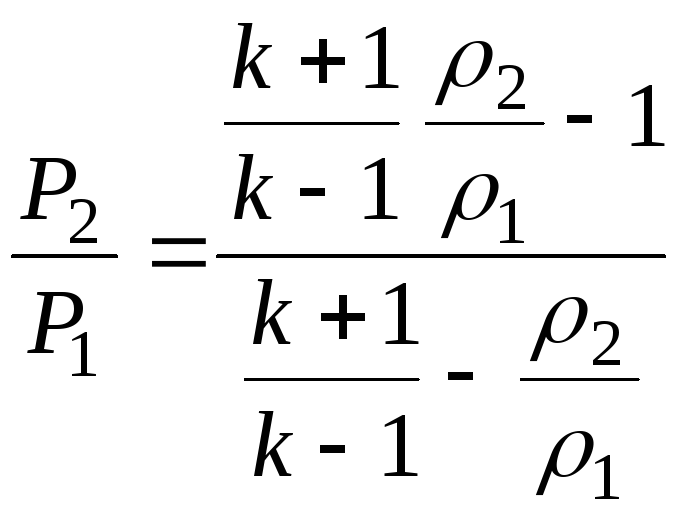в отличие от уравнения адиабаты Пуассона для изоэнтропического процесса. Из уравнения ударной адиабаты следует, что при получим . Для изменения на скачке относительных скоростей, учитывая постоянство в течении, будет иметь место соотношение

или ,

где .

Тогда из уравнения сохранения массы получим

, .

Далее ,

или через : .

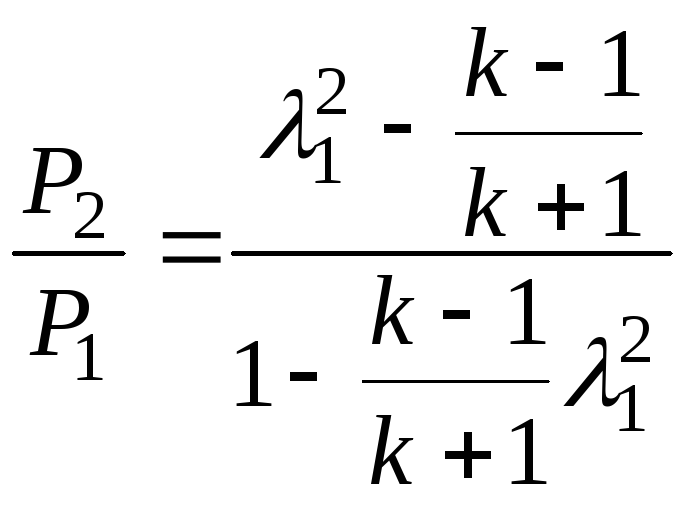Изменение параметров торможения за прямым скачком , определяется следующими формулами:

;

.

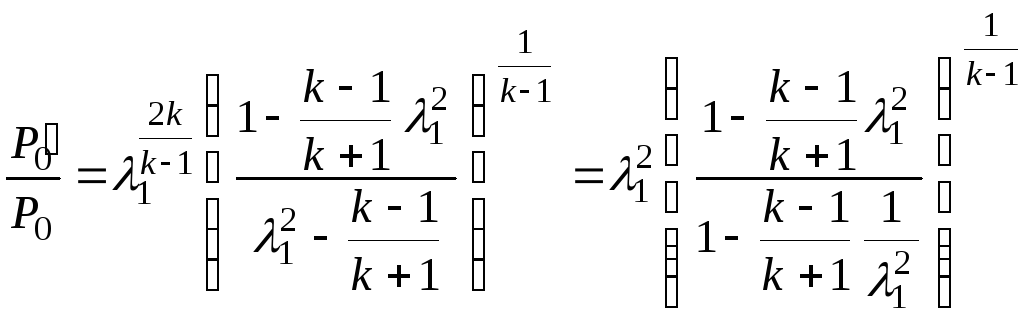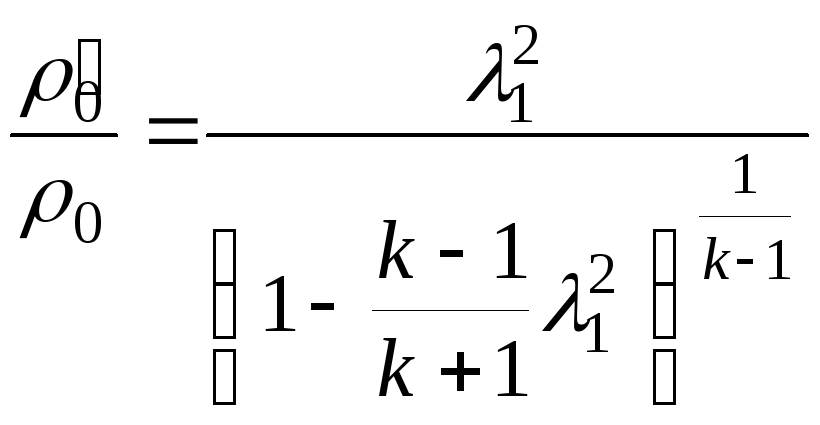Если воспользоваться обозначениями , , то, учитывая что , будет

.

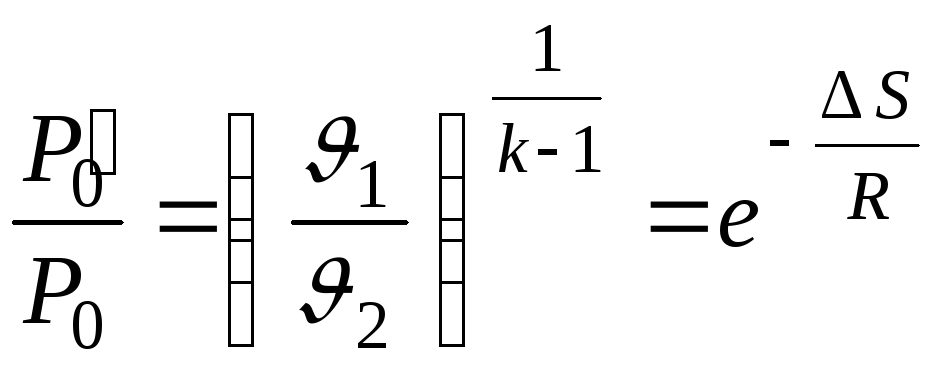Косой скачок давления

Более общим случаем, важным для объяснения структуры сверхзвуковой струи, является косой скачок уплотнения. Для сверхзвуковых струй он реализуется, например, на срезе сопла при неравенстве давления в струе внешнему давлению : , отражении волн разрежения от свободной поверхности струи, а также при натекании сверхзвуковой струи на наклонную преграду.

Исходя из последнего случая, это течение рассматривается в разделе 5.1 на примере построения ударной поляры. В настоящем разделе отмечаются некоторые свойства косого скачка и приводятся основные формулы.

При косом скачке свойства прямого скачка проявляются для составляющей скорости набегающего потока , нормальной к поверхности скачка – , а составляющая скорости, параллельная плоскости скачка , переходит через плоскость скачка без изменения. Схема течения для скачка, присоединенного к наклонной поверхности (регулярное отражение) представлена на рис.2.2.

В этом случае вектор скорости после скачка будет параллелен наклонной поверхности. При больших углах стенки угол наклона вектора будет меньше угла клина , а скачок отойдет от вершины угла и будет иметь прямой участок, начиная с поверхности натекания (нерегулярное отражение). Основная часть скачка будет иметь угол больший вплоть до перехода в прямой скачок.

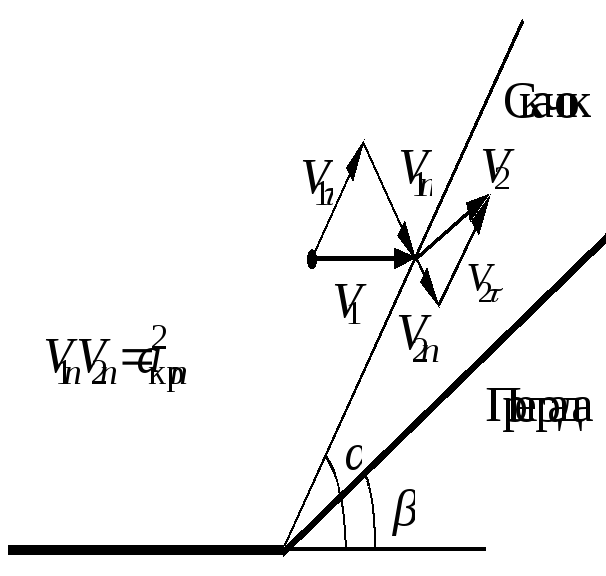
Рис.2.2. Схема течения при регулярном отражении

В соответствии со схемой течения, все зависимости прямого скачка будут справедливы для нормальных составляющих течения с косым скачком. При этом зависимости типа

;

(где ; – скорость звука) определяются через параметры частичного торможения , . Для этого из вектора скорости вычитается переходящая через скачок в неизменном виде составляющая . Тогда критическая скорость звука течения с частичным торможением будет определяться из уравнения энергии следующим образом:

;

.

Из последнего равенства выражаем

.

С использованием этого равенства выводим зависимости для скачка с углом наклона к вектору начальной скорости:

;

.

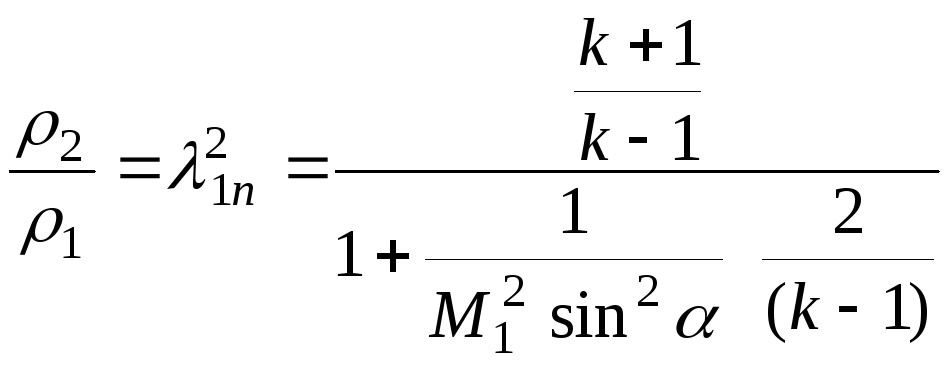Если задано , то наклон скачка можно определить по формуле

,

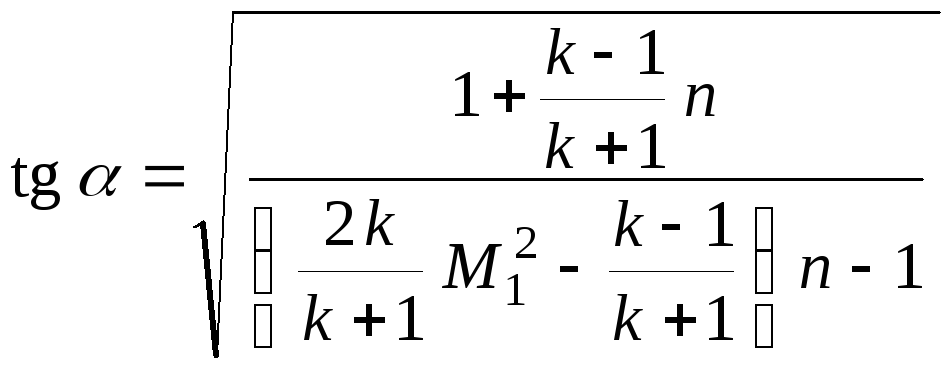тогда для регулярного отражения

.

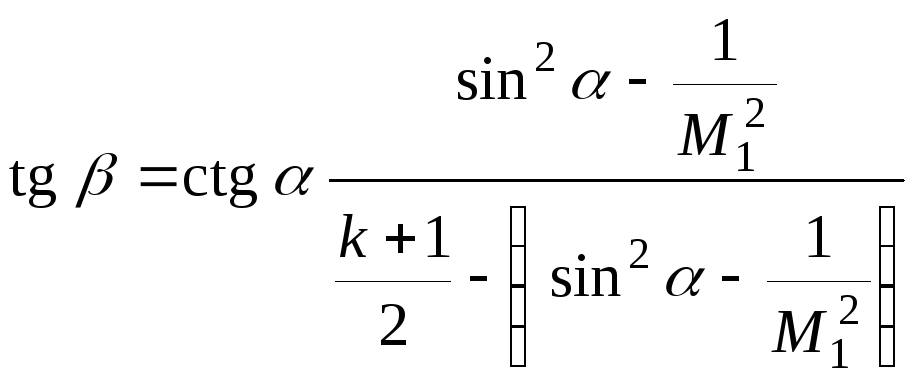Угол наклона скачка уплотнения , соответствующий максимальному углу поворота потока при переходе через скачок , определяется зависимостью от

.