
- •Типовой расчет № 1 Вариант №1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Вариант № 6
- •Вариант № 7
- •Вариант № 8
- •Вариант № 9
- •Вариант № 10
- •Вариант № 11
- •Вариант № 12
- •Вариант № 13
- •Вариант № 14
- •Вариант № 15
- •Вариант № 16
- •Вариант № 17
- •Вариант № 18
- •Вариант № 20
- •Вариант № 21
- •Вариант № 22
- •Вариант № 23
- •Вариант № 24
- •Вариант № 25
- •Вариант № 26
- •Вариант № 27
- •Вариант № 28
- •Вариант № 29
- •Вариант № 30
- •Вариант № 31
- •Вариант № 32
Вариант № 9
-
Тело брошено вертикально вверх со скоростью 20 м/с. Через сколько времени от начала движения оно упадет обратно? На какую высоту оно поднимется? Найдите перемещение и путь тела за 4 секунды движения.
-
Шарик, подвешенный на нити, имеющий длину
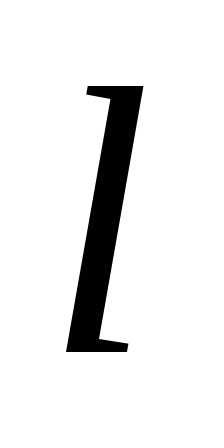 ,
описывает
окружность в горизонтальной плоскости.
Нить составляет с вертикалью угол
,
описывает
окружность в горизонтальной плоскости.
Нить составляет с вертикалью угол
 .
Найти период
.
Найти период
 обращения шарика, если маятник находится
в лифте, движущимся с постоянным
ускорением
обращения шарика, если маятник находится
в лифте, движущимся с постоянным
ускорением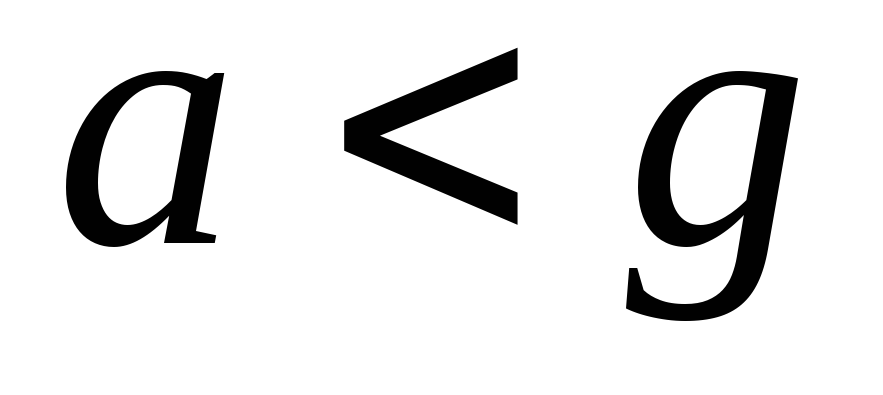 ,
направленным вниз.
,
направленным вниз. -
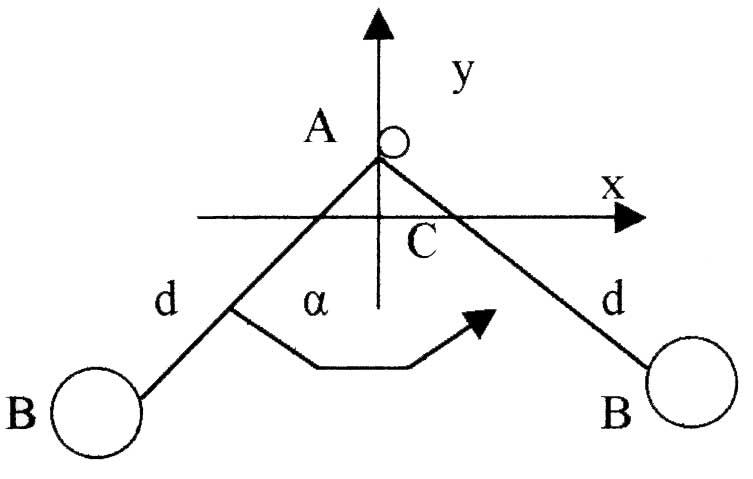
Определите моменты инерции
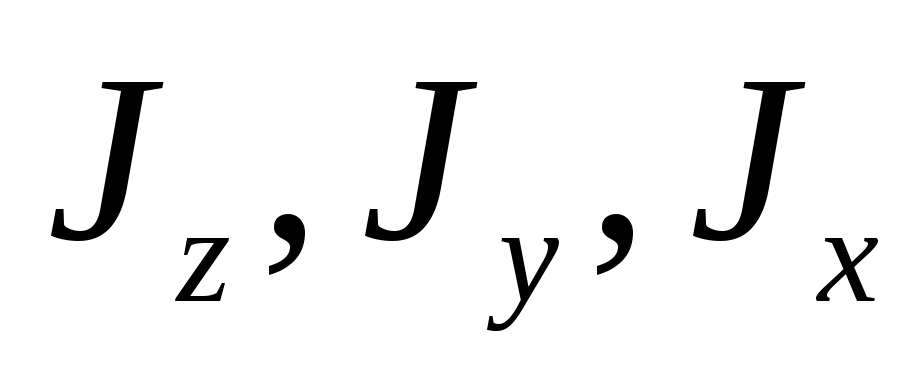 трёх атомных молекул типа
трёх атомных молекул типа
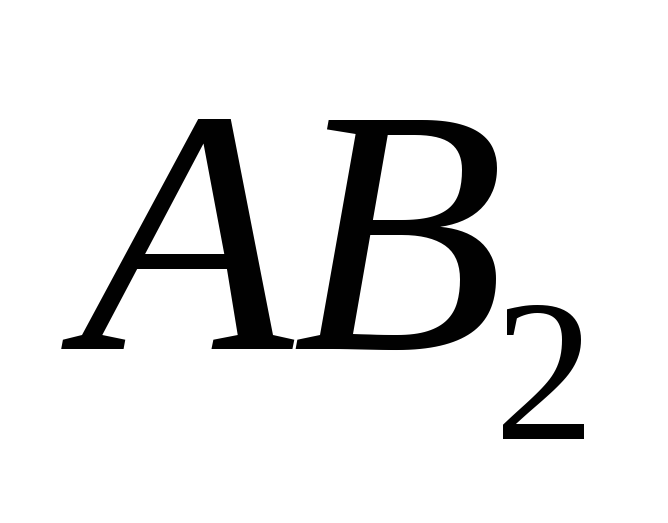 относительно
осей х, у, z
проходящих через центры инерции С
молекулы. Положение осей х и у указаны
на рисунке. Ось z
перпендикулярна плоскости ху. Вычисления
выполнить для следующих молекул: 1)
относительно
осей х, у, z
проходящих через центры инерции С
молекулы. Положение осей х и у указаны
на рисунке. Ось z
перпендикулярна плоскости ху. Вычисления
выполнить для следующих молекул: 1) ;
2)
;
2)
 ;
3)
;
3)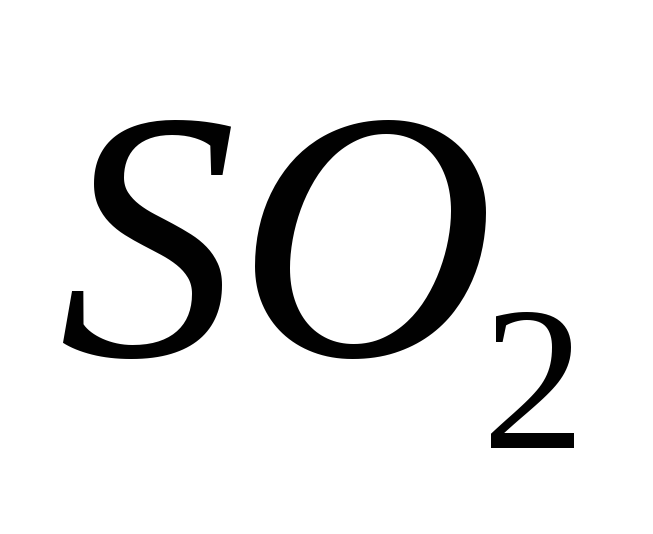 ;
4)
;
4)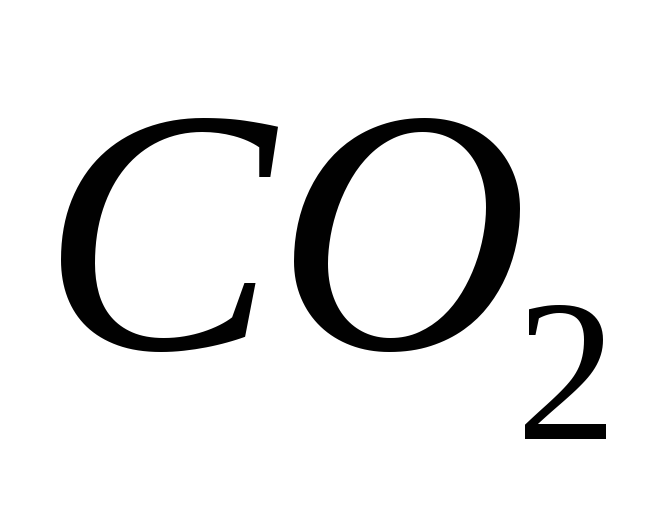 .
Межъядерные
расстояние d
(d
= AB)
и валентные углы
.
Межъядерные
расстояние d
(d
= AB)
и валентные углы :
1)
:
1)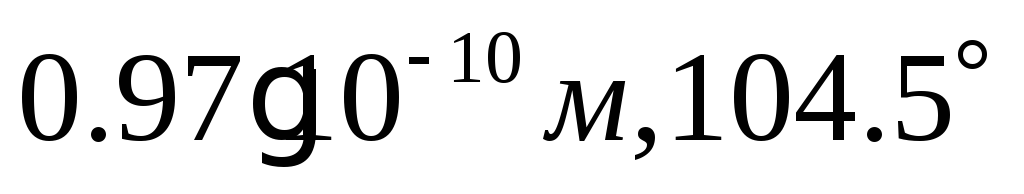 ;
2)
;
2)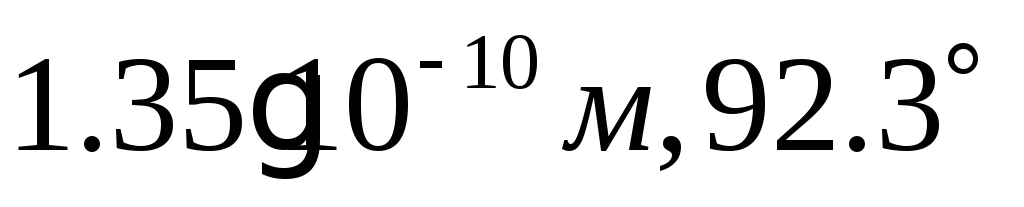 ;
3)
;
3)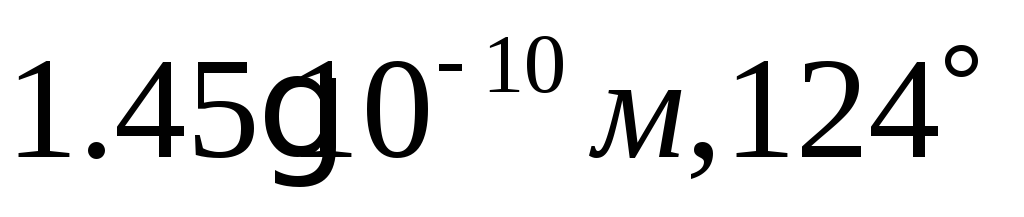 ;
;
4)
![]()
Вариант № 10
-
Тело бросили под углом
 к горизонту с начальной скоростью
к горизонту с начальной скоростью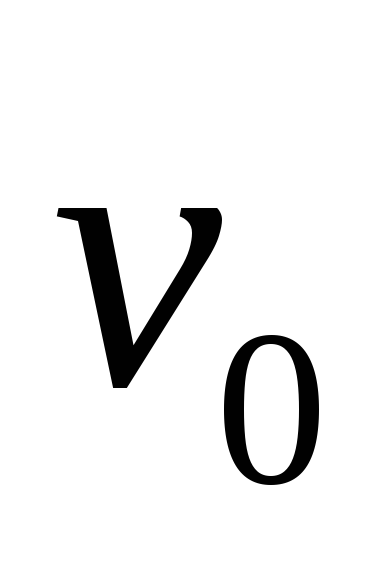 .
Пренебрегая
сопротивлением воздуха, найти:а)
время полета; б) максимальную высоту
подъема и горизонтальную дальность
полета; в) уравнение траектории у(х),
где
у
и
х
- перемещения
тела по вертикали и горизонтали
соответственно; г) радиусы кривизны
начала и вершины траектории.
.
Пренебрегая
сопротивлением воздуха, найти:а)
время полета; б) максимальную высоту
подъема и горизонтальную дальность
полета; в) уравнение траектории у(х),
где
у
и
х
- перемещения
тела по вертикали и горизонтали
соответственно; г) радиусы кривизны
начала и вершины траектории. -
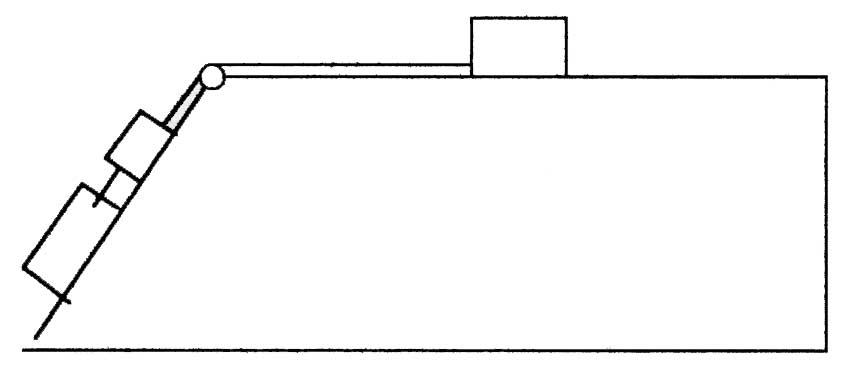
Наклонная доска, составляющая с горизонтом угол 60°, приставлена к горизонтальному столу. Три груза массой по 1 кг каждый соединены невесомой нерастяжимой нитью, перекинутой через неподвижный и невесомый блок, и могут перемещаться соответственно по доске и столу. Найти силу натяжения нити и ускорение системы, если коэффициент трения тел о поверхности доски и стола одинаков и равен 0,3.
-
Вычислить моменты инерции
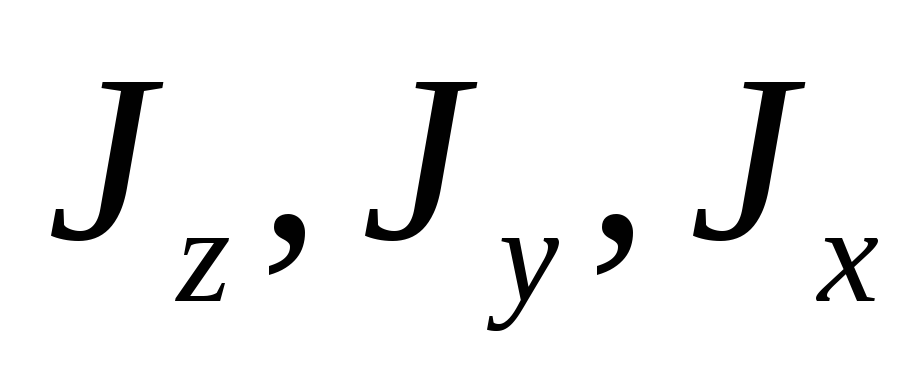 четырёх атомной Т - образной молекулы
четырёх атомной Т - образной молекулы
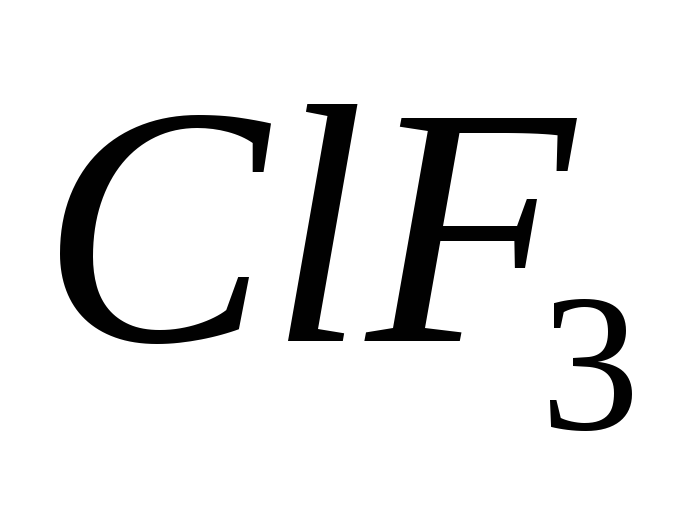 относительно осей x,y,z,
проходящей через центр инерции С
молекулы. Положение осей х и у указаны
на рисунке. Ось z
перпендикулярна плоскости ху. Межъядерные
расстояния d
считать
известными:
относительно осей x,y,z,
проходящей через центр инерции С
молекулы. Положение осей х и у указаны
на рисунке. Ось z
перпендикулярна плоскости ху. Межъядерные
расстояния d
считать
известными:
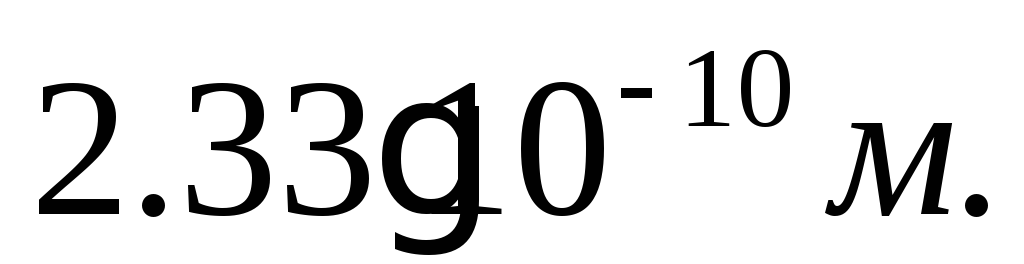
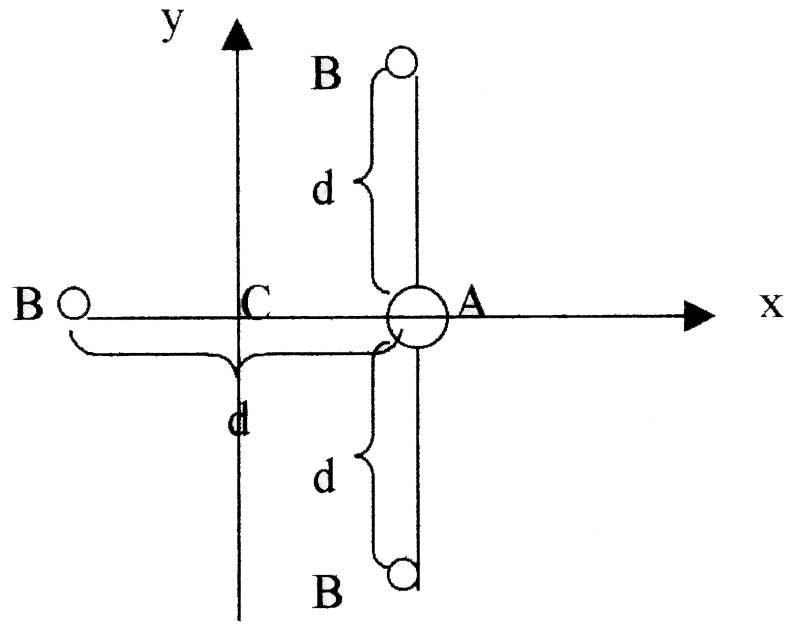
Вариант № 11
-
С башни высотой Н = 25м горизонтально брошен камень со скоростью
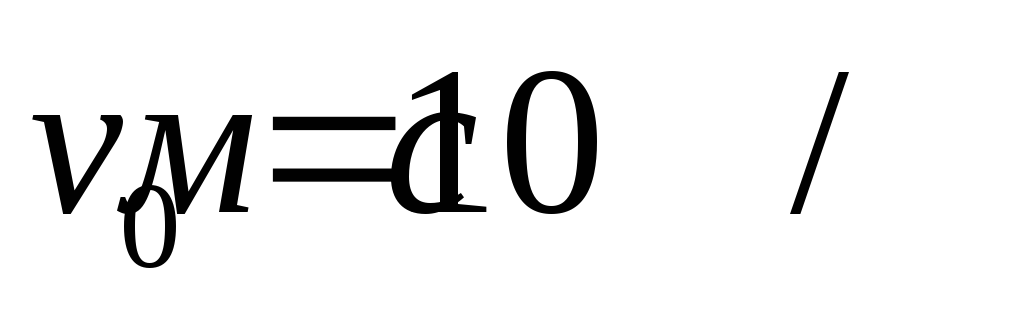 .
На каком расстоянии от основания башни
он упадет? Какова его начальная скорость?
Какой угол образует вектор конечной
скорости с горизонтом?
.
На каком расстоянии от основания башни
он упадет? Какова его начальная скорость?
Какой угол образует вектор конечной
скорости с горизонтом? -
Груз массы m = 200г, привязанный к нити длиной
 ,
вращают в горизонтальной плоскости
с постоянной скоростью так, что нить
описывает коническую поверхность. При
этом угол отклонения нити от вертикали
,
вращают в горизонтальной плоскости
с постоянной скоростью так, что нить
описывает коническую поверхность. При
этом угол отклонения нити от вертикали
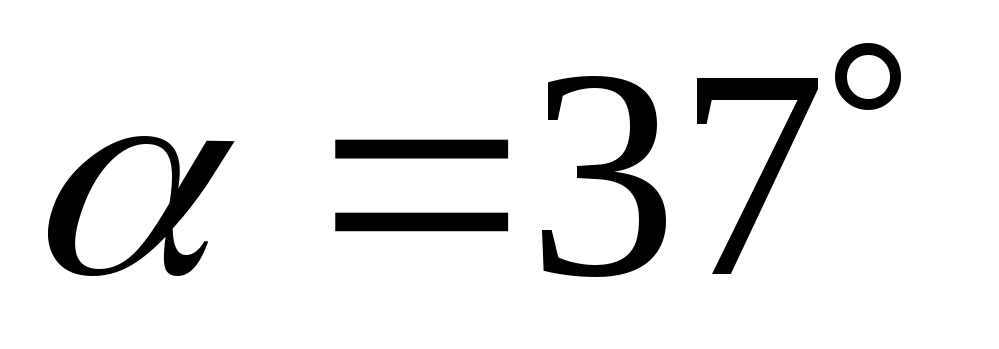 .
Найти угловую скорость со вращения
груза и силу натяжения нити.
.
Найти угловую скорость со вращения
груза и силу натяжения нити. -
Вычислить моменты инерции Iz тонкого однородного стержня длинной
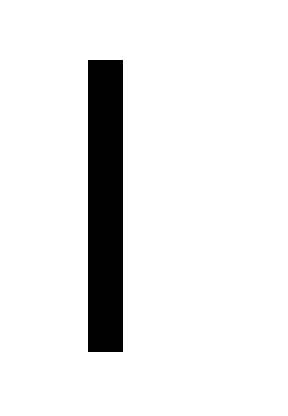 =1
м массой m =1.2 кг относительно оси z,
перпендикулярной стержню и проходящей
через точку О, лежащую на оси стержня.
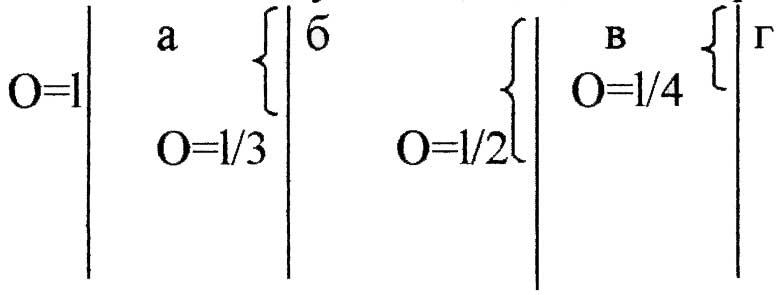
Вычисление выполнить для случаев а, б,
в, г, изображенных на рисунке:
=1
м массой m =1.2 кг относительно оси z,
перпендикулярной стержню и проходящей
через точку О, лежащую на оси стержня.
Вычисление выполнить для случаев а, б,
в, г, изображенных на рисунке:
Вариант № 12
-
Два тела бросили одновременно: одно - вертикально вверх со скоростью
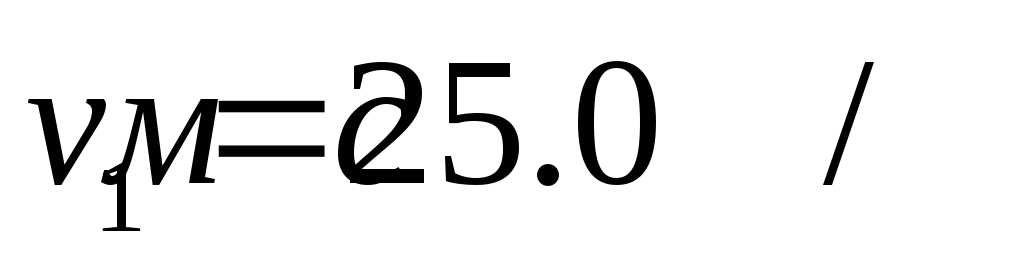 ,
другое - под углом
,
другое - под углом
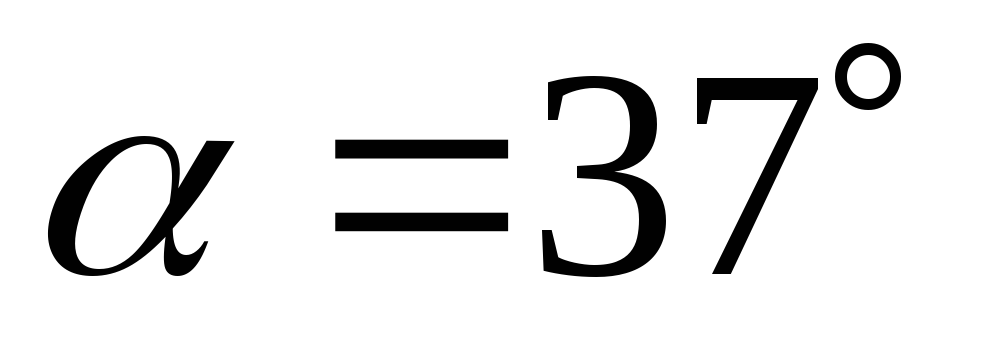 к
горизонту со скоростью
к
горизонту со скоростью
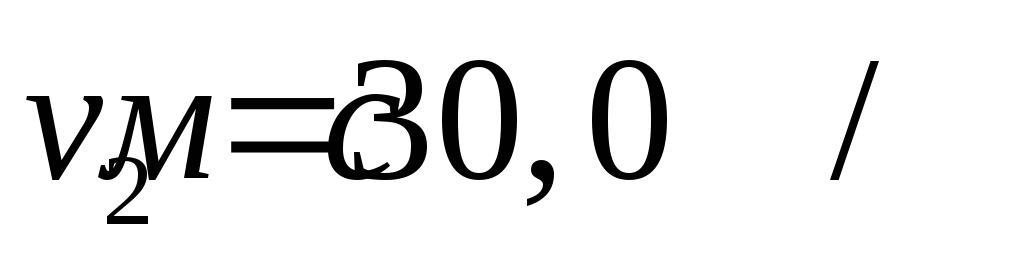 .
Пренебрегая сопротивлением воздуха,
найти их относительную скорость во
время движения.
.
Пренебрегая сопротивлением воздуха,
найти их относительную скорость во
время движения. -
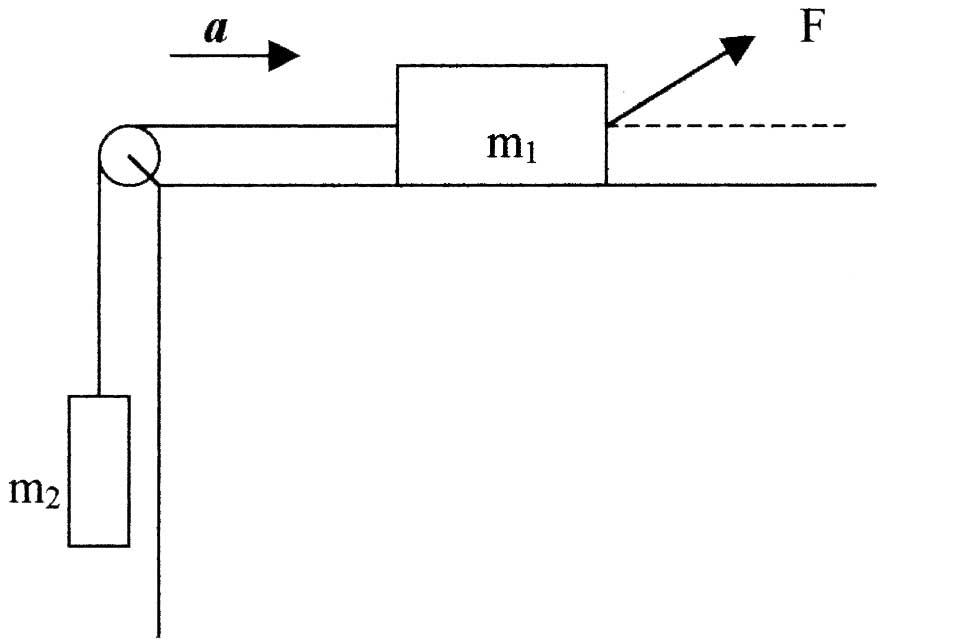
Определить ускорение тел в системе, показанной на рисунке. Коэффициент трения между телом
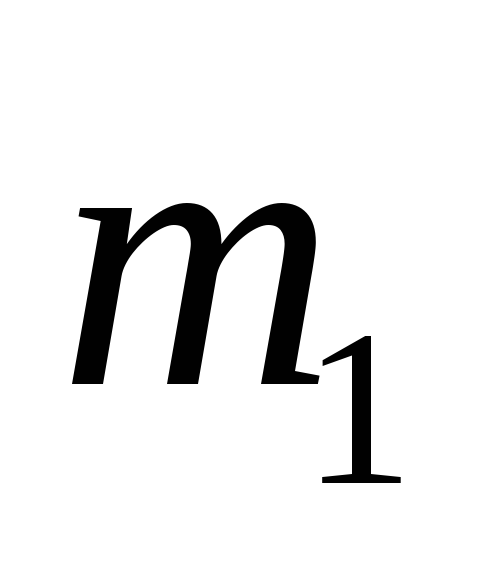 и плоскостью
и плоскостью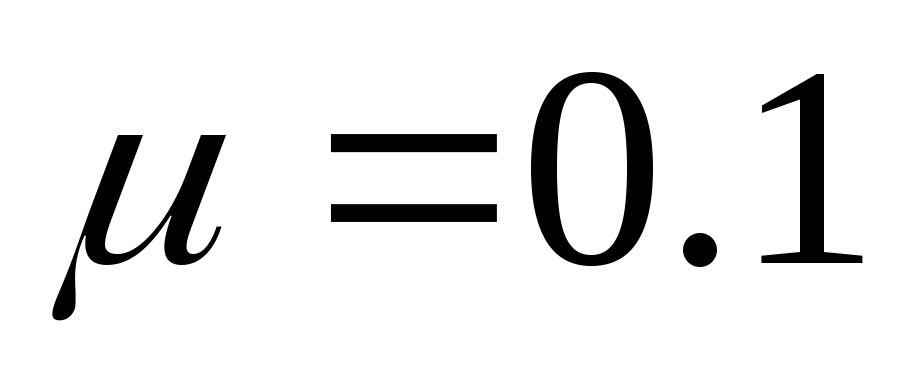 .
Массой блока и нити можно пренебречь.
Нить нерастяжима. Масса грузов
.
Массой блока и нити можно пренебречь.
Нить нерастяжима. Масса грузов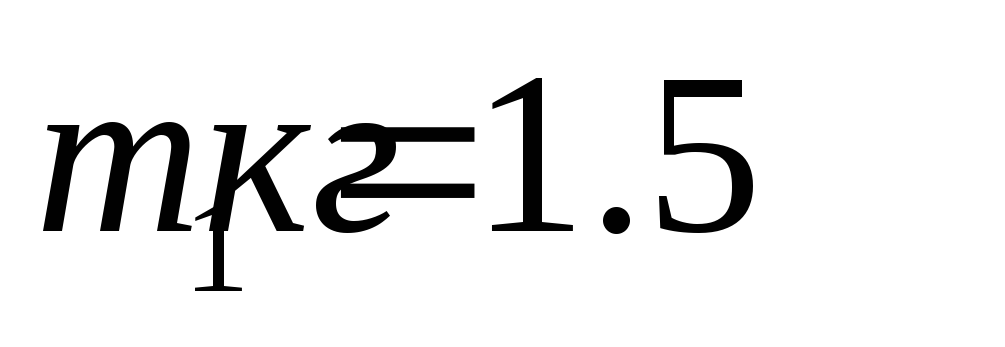 ,
,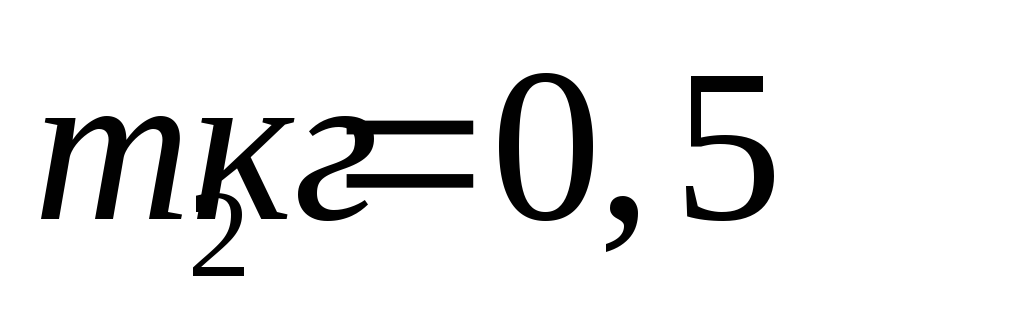 ,
сила F
образует угол
,
сила F
образует угол =30° к горизонту, а ее модуль равен 10 H.
=30° к горизонту, а ее модуль равен 10 H.
-
Вентилятор вращается с частотой 900 об/мин. После выключения вентилятор, вращаясь равно замедленно, сделал до остановки N=75 оборотов. Работа сил торможения равна А = 44Дж. Найти: 1) момент инерции J вентилятора; 2) момент сил торможения М.
