4.5. Комплексные числа, их геометрическая интерпретация, осн.Св-ва.

=-1

x1,x2 = ; =I – мнимая единица

=-1z=a+bi; a,b , R- мнимая единица – комплексное число

a – действительная часть компл.числа, b- мнимая часть z

- a-bi – сопряженное z

z*=

Комплексные числа – вся плоскость, кроме оси ОХ

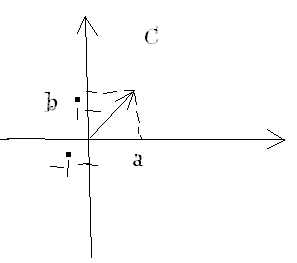z=a+bi

4.7Линейные нердн. Ур-ния 2-го порядка

ур-ние вида: у”+py’+qy=f(x)(1) (f(x)не =0)

теорема: общ реш ур-ния 1 наход по формуле y=Z+Y, где Z=c₁y₁+c₂y₂ – общ реш соответств однор ур-ния. У-частное реш неоднор ур-ния(1)(без док-ва).

Линейные неоднородные ДУ второго порядка с постоянными коэффициентами и спец-й правой частью. y”+py’+py=P_n(x), где ; P_n(x)-многочлен в степ n

1) не явл корнем характер ур-ния k²+pk+q=0

тогда частн реш исходн ур-ния исчем в виде Y=Q_n(x), Q_n(x)- мнг-лен степ n с неопред коэф

2) - явл однокр корнем характ ур-ния . Частн реш: Y=xe

3) - двукр корень характ ур-ния Частн реш: Y= x²e

5.2Сумма ряда.

Пусть дан числовой ряд а₁+а₂+а₃+...+а_n...

Составим суммы

S₁=a₁; S₂=a₁+a₂; S₃=a₁+a₂+a₃; S _n=a₁+a₂+…+a_n

Суммой S₁, S₂,…,S _n - называются частичными суммами ряда, Они образуют бесконечную числовую последовательность.

1. Если существует lim S _n равный S, то говорят, что ряд n →∞ сходится и его сумма равна S.

2. Если Lim S _n не существует или равен бесконечности n →∞ , то говорят, что ряд расходится.

Гармонический ряд.

1+1/2+1/3+…+1/n+…

Докажем, что гармонический ряд расходится: предположим, что он сходится и имеет сумму S. Тогда (S_2n-S_n) = S-S =0,

1+1/2+1/3+1/4+…+1/n+…, (S_2n-S_n) = 0,S_2n-S_n1+1/2+1/3+1/n+1/(n+1)+1/(n+2)+…+1/2n-(1+1/2+1/3+1/4+…+1/n) = 1/(n+1)+1/(n+2)+…+1/(n+n)>n*1/2n = ½,

S_2n-S_n>1/2, (S_2n-S_n) ≠ 0 (не может быть равен 0).

Мы пришли к противоречию, из чего следует, что гармонический ряд расходится.

5.1 Понятие числового ряда и сумма ряда.

Пусть дана последовательность а₁, а₂, а₃,…, а_n ... Выражение а₁+а₂+а₃+...+а_n... называется числовым рядом. Числа а₁, а₂, а₃ – называются членами ряда, а_n - общий член ряда (n –ый член ряда)

1+1\2+1\4+1\8+1\16+...+1\2ⁿ+…=2

1\2+1\4+1\8+1\16+…+1\2ⁿ +...=1

Геометрический ряд.

Члены этого ряда образуют геометрическую прогрессию со знаменателе q

b₁+b₁q+b₁q²+b₁q³+…+b₁q^n-1+…

1) │q│< 1 S _n =

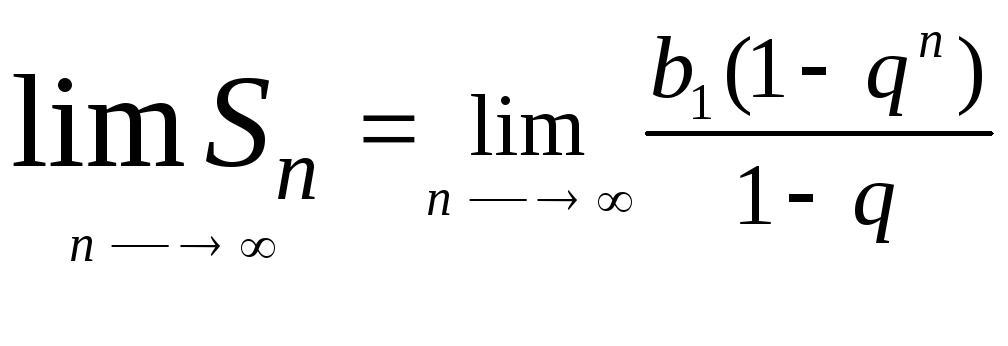= = /т.к.!q!<1/ =

Ряд сходится и его сумма S=, если│q│<1.

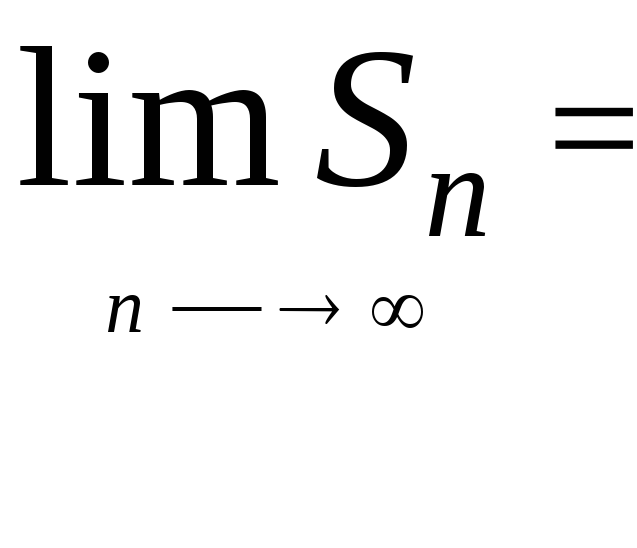
2) │q│>1 =+∞ (т.к. │q│>1)

3) q = 1

5.3 Необходимый признак сходимости.

Если ряд а_n сходится, a_n=0

Доказательство:

S_n = a₁+a₂+…+a_n , S_n-1 = a₁+a₂+…+a_n-1, следовательно an = S_n-S_n-1 = a_n = S_n – S_n-1 = S-S=0, ч.т.д.

Следствие:

Если a_n не равно нулю, то ряд расходится. Доказательство:

Если предположить в этом случае, что ряд сходится, то из необходимого признака следует, что a_n = 0, что противоречит условию.Гармонический ряд.

1+1/2+1/3+…+1/n+…

Докажем, что гармонический ряд расходится: предположим, что он сходится и имеет сумму S. Тогда (S_2n-S_n) = S-S =0,

1+1/2+1/3+1/4+…+1/n+…, (S_2n-S_n) = 0,