5.6Знакопеременные ряды. Абсолютная и условная сходимость.

Ряд наз-ся знакопеременным, если его членами являются действительные числа произвольного знака.

Пусть дан знакопеременный ряд a₁+a₂+…+a_n+…=(1), где числа a₁, a₂,…, a_n,… могут быть как положительными, так и отрицательными. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда: (2).

Определение: Если сходится ряд (2), то ряд (1) наз-ся абсолютно сходящимся. Если ряд (1) сходится, алгоритм ряд (2) расходится, то ряд (1) называется условно(или неабсолютно) сходящимся.

Теорема: Если знакопеременный ряд абсолютно сходится, то он сходится.

Док-во: Пусть знакопеременный ряд (1) абсолютно сходится. Это значит, что сходится ряд (2). Обозначим через S_n частичную сумму ряда (1), алгоритм через σ_n – частичную сумму ряда (2):

Т.к. ряд (2) сходится, то последовательность {σ_n} его частичных сумм имеет предел , причем σ_n≤σ n (3), т.к. члены ряда (2) положительны. Обозначим далее через сумму положительных членов, алгоритм через -- сумму абсолютных величин отрицательных членов, содержащихся в сумме S_n. Тогда:

(4)

(5)

Из рав-ва (5) следует, что {} и {} монотонно возрастают при возрастании n, алгоритм из (3) – что они являются ограниченными; Следовательно, существуют пределы

Тогда в силу равенства (4) последовательность частичных сумм ряда (1) имеет предел

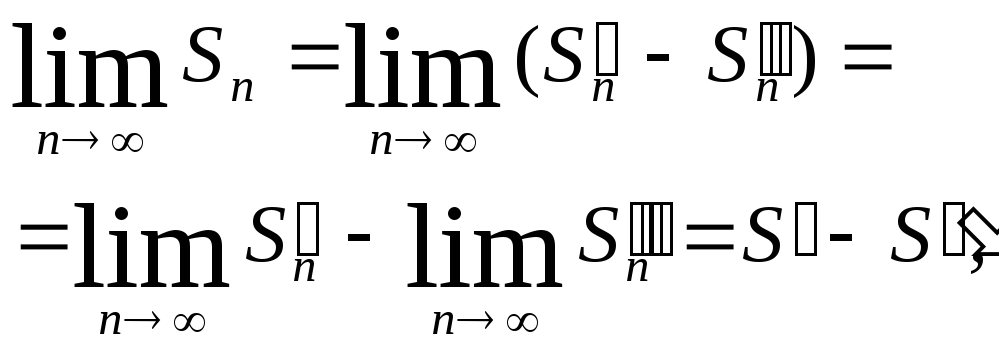
алгоритм это значит, что ряд (1) сходится.

6.2.Теорема Абеля.

1) Если степенной ряд  a_nxⁿ сходится при x=x₀, то он сходится причем абсолютно для всех x , удовлетворяющих неравенству |x|<|x₀|

2) Если же ряд a_nxⁿ расходится при x=x_{1 ,} то он расходится при всех x , удовлетворяющих условию |x|>|x₁|

Док-во (основано на свойствах последовательностей).

1)Так как числовой ряд a_nx₀ⁿ сходится, то a_nx₀ⁿ =0. Это означает, что числовая последовательность {a_nx₀ⁿ} ограничена.Тогда перепишем степенной ряд в виде

a₀ + a₁x₀ (x/x₀) + a₂x₀²(x²/x₀²) +…+…= a_nx₀ⁿ (x/x₀)²

Рассмотрим ряд из абсолютных величин.

|a₀| + |a₁x₀ (x/x₀) | + |a₂x₀²(x²/x₀²) | +…+…<= M + M| x/x₀| + M| x/x₀|² +…= M(1+q+ q²+…)

Это геометрическая прогрессия с q=(x/x₀)<1—сходится. Из признака сравнения следует абсолютная сходимость степенного ряда.

2) 2-ая часть теоремы. От противного. Пусть степенной ряд сходится при некотором x^*, | x^*|> x_1. Но тогда согласно 1-ой части теоремы, степенной ряд сходится для всех | x |< x^* . В том числе должен сходится

и при x= x₀, так как | x |< | x^*| . Но это противоречит

предположению теоремы. Теорема доказана.