
4. Гидростатическое давление
Гидростатическое давление - напряжение, возникающее в жидкости под действием сжимающих сил.
4.1. Свойства гидростатического давления
Давление обладает двумя основными свойствами:
4. 1.1. Давление в точке действует нормально к площадке действия и является сжимающим, то есть оно всегда направлено внутрь того объема жидкости, давление на который мы рассматриваем (первое свойство гидростатического давления).
Может ли гидростатическое давление быть направлено не по нормали? Если гидростатическое давление направлено не по нормали, то его можно разложить на нормальную и касательную составляющие. В соответствии с законом трения Ньютона касательные напряжения возникают при наличии градиента скорости, а мы рассматриваем покоящуюся жидкость (или другими словами, касательные напряжения должны привести к движению слоев жидкости, а мы рассматриваем покой).
Таким образом, давление в покоящейся жидкости может быть направлено только по нормали.
Особыми физическими опытами доказано, что покоящаяся жидкость в определенных условиях иногда способна сопротивляться равномерному всестороннему растяжению. В обычных условиях растяжение жидкости будет отличаться от равномерного всестороннего, поэтому в ней будут возникать касательные напряжения и жидкость будет течь под действием растягивающих усилий. Кроме того, в обычных условиях даже при небольших растягивающих усилиях при всестороннем растяжении возникает разрыв (образование прогазовой прослойки) в жидкости.
Имея это в виду, считают, что в обычной практической обстановке жидкость не сопротивляется касательным и растягивающим усилиям. Учитывая это, очевидно, следует сделать вывод, что давление в покоящейся жидкости всегда направлено по нормали к площадке действия внутрь рассматриваемого объема жидкости.
4.1.2. Величина давления в данной точке не зависит от угла наклона площадки действия по отношению к координатным осям (второе свойство гидростатического давления).
Докажем последнее утверждение. Рассмотрим равновесие объема жидкости в виде тетраэдра с ребрами, параллельными координатным осям и соответственно равными dx, dy, dz (Рис. 4.1.1). Пусть в выделенном объеме действует единичная массовая сила, составляющие которой равны X, Y, Z. Обозначим гидростатические давления, действующие на грани тетраэдра, параллельные координатным осям соответственно px, py и pz, а давление на наклонную грань – pn. Отметим, что все эти давления направлены по нормалям к соответствующим площадкам. Площадь наклонной грани обозначим dω. Запишем уравнение равновесия выделенного объема жидкости вдоль оси x.
Рис.
4.1.1.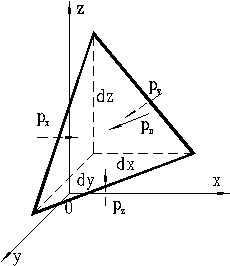
Проекция массовых сил на оси x, y, z
dFmx = Xdm,
dFmy = Ydm,
dFmz = Zdm,
где dm – масса жидкости в тетраэдере.
Масса тетраэдера равна произведению его объёма на плотность жидкости ρ
dm
=
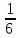 ρdxdydz.
ρdxdydz.
Тогда силы гидростатического давления, действующие на грани тетраэдра выразим с:
dFx
 px
dydz;
px
dydz;
dFy
=
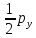 dxdz;
dxdz;
dFz
=
 pzdxdy.
pzdxdy.
Гидростатическое давление, действующее на наклонную грань тетраэдра обозначим через pп, а площадь этой грани – через dω. Давление pп нормально к этой грани. Обозначим направление вектора pп к наклонной грани через углы α, β и φ, которые образуют нормали к осям координат.
Составим уравнение равновесия внутреннего объёма жидкости в направлении оси x.
Проекция сил давления
dFx
-
dFxп
=
 dydz
– pп
dω
dydz
– pп
dω .
.
Уравнение равновесия тетраэдра с учетом массовых сил
dFx - dFxп +dFmx = 0
или
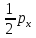 dydz
– pп
dω
dydz
– pп
dω +
+ Xdxdydz
= 0.
Xdxdydz
= 0.
Проекция наклонной грани на плоскость y0z
dω
 =
=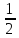 dydz.
dydz.
Разделим полученное уравнение равновесия на элементарную площадь
 dydz.
dydz.
Таким образом будем иметь
px
- pп
+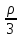 Xdx
= 0.
Xdx
= 0.
При стремлении размеров тетраэдра dx к нулю
 Xdx
= 0.
Xdx
= 0.
Следовательно, в пределе получим
px = pп..
Уравнение равновесия в направлении осей y и z
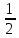 py
dxdy
– pп
dω
py
dxdy
– pп
dω
 +Y
+Y
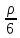 dxdydz
= 0;
dxdydz
= 0;
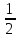 pz
dxdy
– pп
dω
pz
dxdy
– pп
dω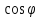 + Z
+ Z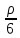 dxdydz = 0.
dxdydz = 0.
После
сокращения соответственно на
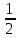 dxdz
и
dxdz
и
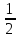 dxdy,
с учетом
dxdy,
с учетом
dω
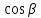 =
=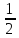 dxdz
и dω
dxdz
и dω
 =
=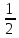 dxdy,
dxdy,
получим
py
–
pп
+
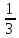 Ydy
= 0;
Ydy
= 0;
pz
–
pп
+
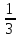 Zdz
= 0.
Zdz
= 0.
В
пределе при dy 0,
dz
0,
dz 0
0
py = pп и pz = pп.,
Следовательно,
px = py = pz =pп.
Таким образом, при стремлении размеров тетраэдра к точке давление в ней по всем направлениям в покоящейся жидкости одинаково.
Следует отметить, что гидростатическое давление в разных точках объёма жидкости зависит от координат этой точки, т.е. давление является функцией координат
P = f(x, y, z).
Давление является сложной функцией, следовательно, дифференциал давления может быть представлен в частных производных
dp
=
 dx
+
dx
+
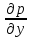 dy
+
dy
+
 dz.
dz.
