14.3.2. Постепенное расширение трубопровода

Плавно расширяющийся трубопровод – диффузор (рис. 14.3.2) широко применяется в технике.

Рис. 14.3.2.

Геометрическими параметрами диффузора является угол α и диаметры d₁ и d_2. У стенок диффузора образуются завихрения. Течение скорости в диффузоре сопровождается ее увеличением и и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α, и, как следствие увеличиваются потери напора.

Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:

h_{дф =} h_расш + h_l.

Потеря напора на расширение может быть найдена по формуле

h_расш.. = .

с введением поправочного коэффициента К_см, называемого коэффициентом смягчения, который зависит от угла конусности

h_расш.. = К_см .

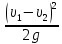Коэффициент местного сопротивления в этом случае определится по формуле

ζ_расш = К_см ζ_{вн. р} = К_см

К_см при α<20° можно принять равным К_см , a при α значение коэффициента К_см следующие:

Угол конусности,	4	8	15	30	60
……..	0,08	0,16	0,35	0,80	0,90

Потери напора на трение по длине определяют по формуле

h_дл =

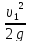
Таким образом, суммарный коэффициент местного сопротивления для диффузора равен

.

Наименьшие потери напора в диффузоре получаются при угле расширения его в пределах от 5 до 10°.

14.3.3. Внезапное сужение трубопровода

Внезапное сужение трубы (рис.14.3.3.1) всегда вызывает меньшую потерю энергии, чем внезапное расширение с таким же соотношением площадей. В этом случае потеря обусловлена, во-первых, трением потока при входе в узкую трубу и, во-вторых, потерями па вихреобразование. Последние вызываются тем, что поток не обтекает входной угол, а срывается с него и сужается. Кольцевое же пространство вокруг суженной части потока заполняется завихренной жидкостью.

υ₁ω₁ υ₂ω₂

рис. 14.3.3.1.

Потери напора можно определить, используя формулу Борда, полагая, что в основном потери будут за сжатым сечением, а до сжатого сечения потери напора существенно малы.

Скорость в сжатом сечении x - x площадью ω_x

υ_с = .

Выразим отношение площадей сжатого сечения и площади узкой части трубы ω₂ через коэффициент сжатия ε (эпсилон)

ε = .

Потери напора по Борду

h_в.суж = .

Из уравнения неразрывности

υ_x ω_x = υ₂ ω_2, υ_x = υ₂ .

Выразим потери напора через скоростной напор

h_в.суж =

или

h_{в суж} = ξ_суж

где ξ_всуж - коэффициент сопротивления внезапного сужения, зависящий от степени сужения.

ζ_всуж = .

Коэффициент сжатия ε зависит от отношения площадей узкой и широкой частей трубы n = и может быть вычислен по формуле А. Альшуля

ε = 0,57 + .

Для практических расчетов можно пользоваться полуэмпирической формулой Идельчика:

ζ_суж = 0,5(1— ω₂/ω₁)/2 =0,5(1—n),

Из формулы следует, что в том частном случае, когда можно считать ω₂/ω₁= 0, т.е. при выходе трубы из резервуара достаточно больших размеров и при отсутствии закруглений входного угла, коэффициент сопротивления

ζ_суж = ζ_вх = 0,5.

Закруглением входного угла (входной кромки) можно значительно уменьшить потерю напора при входе в трубу.