
Весна 16 курс 3 ОрТОР / Гидравлика / lektsia__10
.docx10.1. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
(УРАВНЕНИЕ ЭЙЛЕРА)
Воспользуемся вторым законом Ньютона применительно к жидкой частице. Произведение массы частицы на ускорение ее центра масс равно сумме всех внешних сил, действующих на частицу. Силы и ускорение будем рассматривать в проекции на оси координат.
Предположим,
что в жидкости движется элементарный
объем в форме параллелепипеда со
сторонами dx,
dy, dz
(см. рис. 10.1). На параллелепипед действуют
поверхностные силы давления и массовые
силы с проекциями X,
Y, Z,
отнесенными к единице массы. При движении
объема возникают силы инерции. Проекции
этих сил на оси координат, отнесенные
к единице массы, равны соответственно:
-
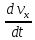 ;
-
;
-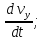 -
-
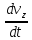
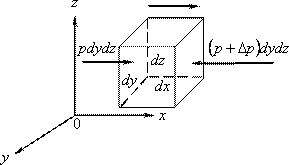
Рис. 10.1.1. Схема равномерного движения объема жидкости
Рассматривая равновесие параллелепипеда, находящегося в движущейся жидкости, используем принцип Даламбера: уравнение движения можно рассматривать как уравнение равновесия, если ввести силы инерции.
Рассмотрим условие равновесия сил, в проекции на ось х. Сила давления на левую грань – pdydz, на правую грань
-(p+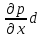 х
х
где
![]() =
Δp–
изменение давления вдоль оси x
(прирацение
давления на единицу элементарной длины
dx)
=
Δp–
изменение давления вдоль оси x
(прирацение
давления на единицу элементарной длины
dx)
Массовая сила равна Xρdxdydz. Уравнение равновесия запишется в виде
pdydz
–(p+ х
х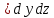 +
Xρdxdydz
+
Xρdxdydz ρdxdydz
=
0,
ρdxdydz
=
0,
или
–
![]() dxdydz+
Xρdxdydz
dxdydz+
Xρdxdydz![]() ρdxdydz
= 0.
ρdxdydz
= 0.
Разделив каждый член уравнения на ρdxdydz, получим
X
-
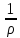
 =
=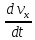
Соответственно для осей y и y уравнение равновесия будет выглядеть следующим образом
Y
–
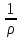
 =
=
Z
-

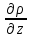 =
=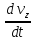
Объединив полученные уравнения, получим систему уравнений Эйлера:
X
-

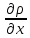 =
=
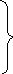
Y
–

 =
=
Z
-
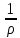
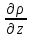 =
=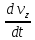
Эта система дифференциальных уравнений движения идеальной жидкости носит название уравнений Эйлера. Они выражают связь между проекциями действующий сил, скоростей, давления и плотности жидкости и очень важны при изучении движения жидкости.
10.2. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ
(УРАВНЕНИЕ НАВЬЕ-СТОКСА)
В невязкой жидкости действуют только нормальные напряжения.
При движении вязкой жидкости в ней возникают не только нормальные, но и касательные напряжения, так как вязкая жидкость обладает способностью оказывать сопротивление относительному сдвигу своих слоев.
Дифференциальные уравнения движения реальной (вязкой) жидкости можно получить, используя уравнение Эйлера для идеальной жидкости, учитывая силы вязкого трения, связанные с напряжениями τ, P.
Эти напряжения зависят не только от координат точки, но и от ориентации площадки действия.
|
|
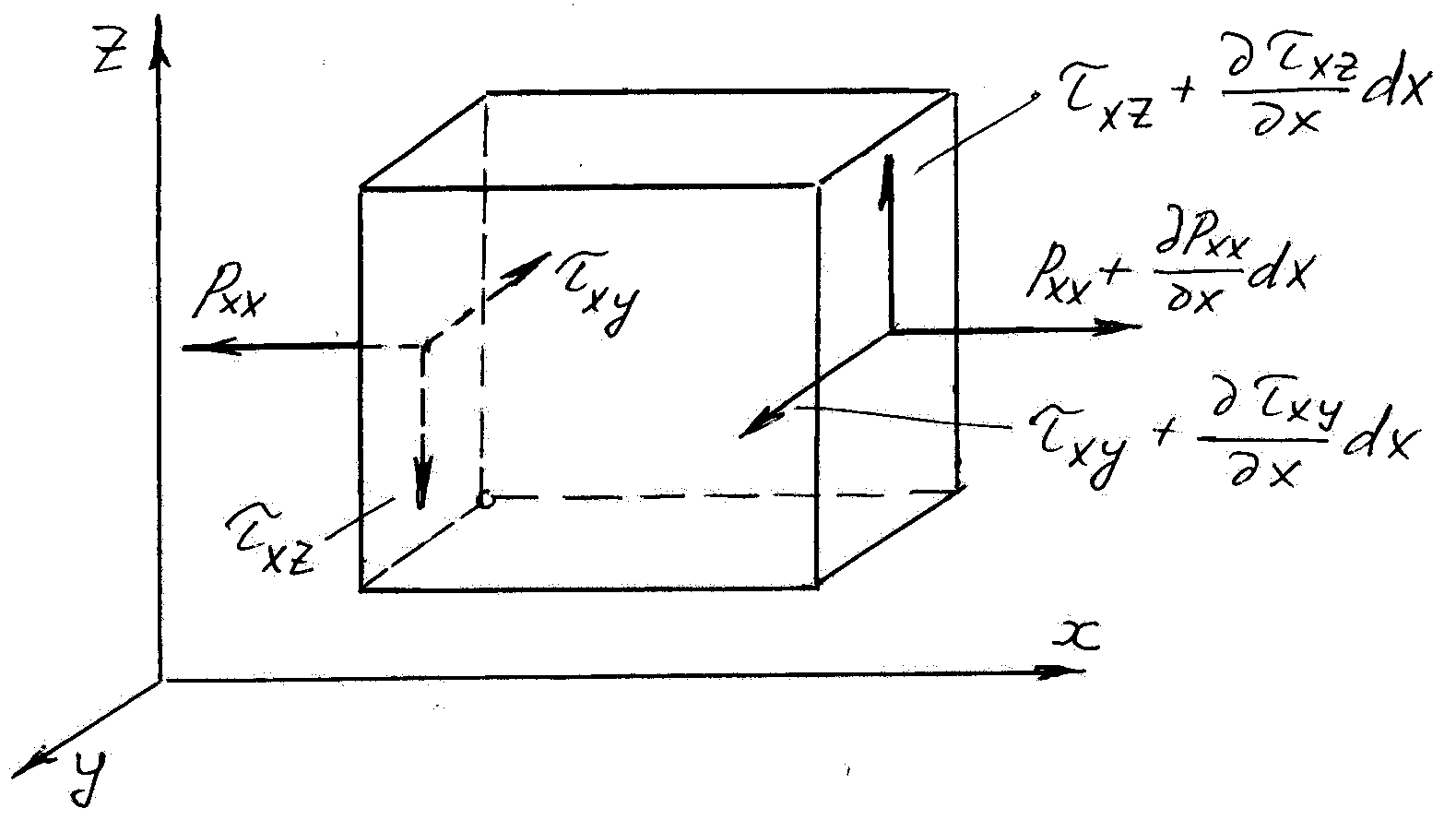
Рассмотрим элементарный параллелепипед с ребрами dx, dy, dz, выделенный в движущейся жидкости (Рис. 10.2.1).
|
Рис. 10.2.1.
Рассмотрим напряжения, возникающие на гранях парраллепипеда. Нормальные напряжения на гранях: P𝑥𝑥, Pyy, Pzz.
Касательные напряжения: τ𝑥𝑥, τyy, τzz.
Первый индекс – направление оси, к которой перпендикулярна данная грань. Второй индекс – направление действия напряжения. На рисунке показаны только напряжения, действующие на левую и правую грани.
На рисунке показаны только напряжения, действующие на левую и правую грани.
|
|
Отметим без доказательства, что касательные напряжения на взаимно перпендикулярных площадках, направленные по нормали к линии пересечения этих площадок, равны друг другу:
Дифференциальные уравнения движения реальной (вязкой) жидкости можно получить, используя уравнение Эйлера для идеальной жидкости, учитывая силы вязкого трения, связанные с напряжениями τ, P.
X
-
Y
–
Z
-
Где
R Поверхностные силы действуют на все шесть граней. Они равны произведению соответствующего напряжение (нормального или касательного) на площадь грани. Рассмотрим эти силы сначала в проекции на ось Χ, записав только силы, проекция которых на ось Χ не равна нулю: Левая
грань и правая:
Задняя
грань и передняя:
Нижняя
грань и верхняя:
После
сокращения и деления на массу получим
dR Без доказательства укажем: в вязкой жидкости сумма нормальных напряжений по трем взаимно перпендикулярным граням не зависит от ориентации этих площадок.
Для
определения
Принимая условия, что нормальные напряжения прямо пропорциональны соответствующим скоростям деформации (скоростям относительного удлинения) и согласно закону Ньютона
Таким образом, частные производные напряжений будут равны:
Подставим полученные выражения в уравнение
dR получим:
dR По аналогии можно определить единичные силы вязкостного трения по направлению осей Οy и Οz:
dR
dR Подставим полученные выражения в систему уравнений
X
-
Y
–
Z
-
с
учетом, что кинематическая вязкость
ν
=
X
-
Y
–
Z
-
Полученные уравнения называются уравнениями Навье-Стокса. Уравнения Навье-Стокса можно представить в более сокращенном виде, используя оператор Лапласа.
Оператор
Лапласа
Тогда
X
-
Y
–
Z
-
В
данном случае единичные силы вязкого
трения
dR
dR
dR Уравнения Навье-Стокса совместно с уравнением неразрывности и уравнением состояния образуют замкнутую систему, которая, однако, не имеет общих решений.
|
|||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||


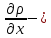 dR
dR =
=
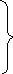
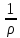
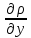 -
dR
-
dR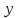 =
=
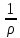
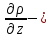 dR
dR =
=
 ,
R
,
R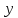 ,
R
,
R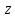 – единичные
силы вязкого трения.
– единичные
силы вязкого трения.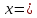
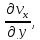
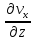 .
.
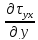 =
μ
=
μ ;
;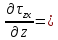 μ
μ
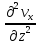 ;
;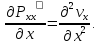

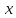 =
=

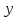 =
=

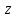 =
=
 .
.
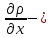 dR
dR =
=
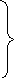
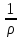
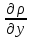 -
dR
-
dR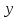 =
=

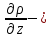 dR
dR =
=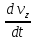
 :
:
 -
-
 =
0;
=
0;

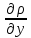 +
ν
+
ν
 -
-
 = 0;
= 0;

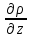 + ν
+ ν

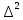 =
=


 ʋ𝑥
-
ʋ𝑥
-
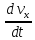 =
0;
=
0;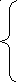

 ʋy
-
ʋy
-
 =
0;
=
0;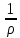
 +
+
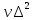 ʋz
-
ʋz
-
 =
0.
=
0.
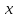 =
=
 ʋ𝑥
;
ʋ𝑥
; ʋy;
ʋy; =
=
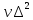 ʋz.
ʋz.