Теоретико—числовые функции №2

Функции и мультипликативны.

Пример: . Действительно, число 20 имеет 6 делителей — 1,2,4,5,10,20.

Замечание: Нельзя забывать взаимной простоты чисел m и n. Например, взять если m = 4 и n = 6 — числа не взаимно простые, то , но . (В действительности )

Определение: Функция f(n) называется вполне мультипликативной, если равенство верно для любых натуральных чисел m и n.

Пример: — вполне мультипликативная функция при любой . Функции , — мультипликативны, но не вполне мультипликативны.

п.4 Функция Мёбиуса

Определение: Функций Мёбиуса называется функция µ(n), заданная на N такая, что

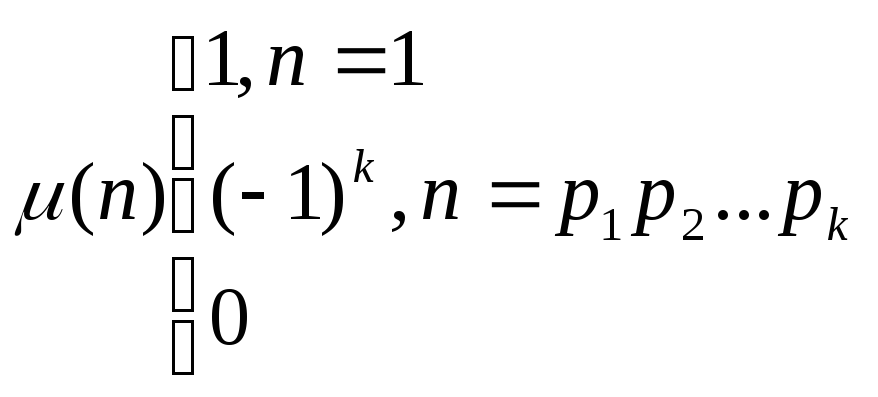
Иначе говоря, µ(n)=0, если в каноническом разложении, хотя бы один показатель . В этом случае говорят, что число n не свободно от квадратов, т.е. представимо в виде .

Пример:

Если p — простое, то, очевидно, µ(p)= -1.

Из определения следует мультипликативность функции µ(n). Это обстоятельство позволяет дать равносильное определение функции Мёбиуса (смотри замечание в пункте 3).

Определение: Мультипликативная функция µ(n) такая, что при , называется функцией Мёбиуса.

Теорема: Пусть f(n) — мультипликативная функция; . Тогда

Доказательство: Произведение µ(n)f(n) мультипликативно (свойство 2, п.3). Применяя к функции теорему из п.3, и учитывая, что и при , получим:

■

Замечание: Если n = 1, то .

Выбирая различные мультипликативные функции f(n) можно получить серию полезных тождеств для функции Мёбиуса. Например,

1)

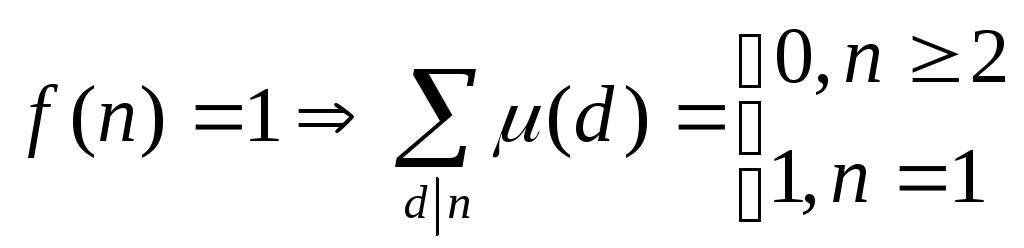
2)

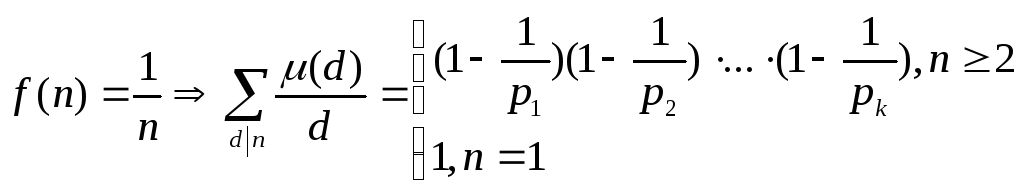
Замечание: Приведем другое доказательство полученных тождеств. Пусть . Перечислим все делители n, для которых

.

Тогда

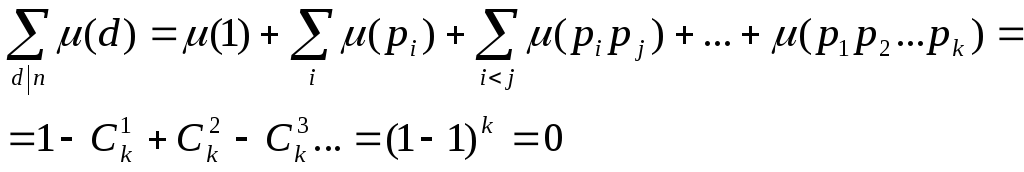
Аналогично,

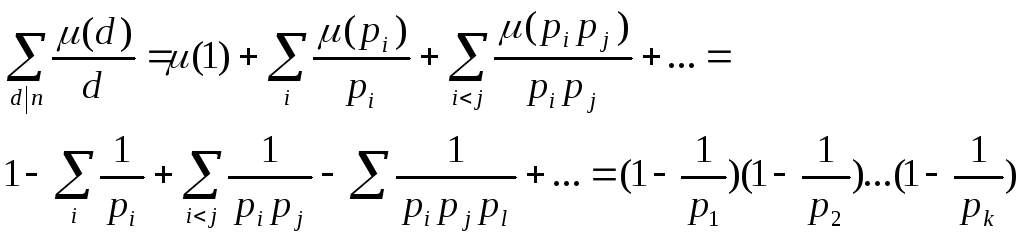
Функция Мёбиуса позволяет установить обратную связь между данной функцией f(n) и функцией

Теорема: (закон обращения Мёбиуса)

Пусть f(n) — произвольная функция, определена на N и

— (1)

Тогда — (2)

Верно и обратное утверждение: если f(n) определена формулой (2), то g(n) вычисляется с помощью (1).

Доказательство: При n=1 имеем и утверждение теоремы верно. Пусть . По определению g(n) имеем:

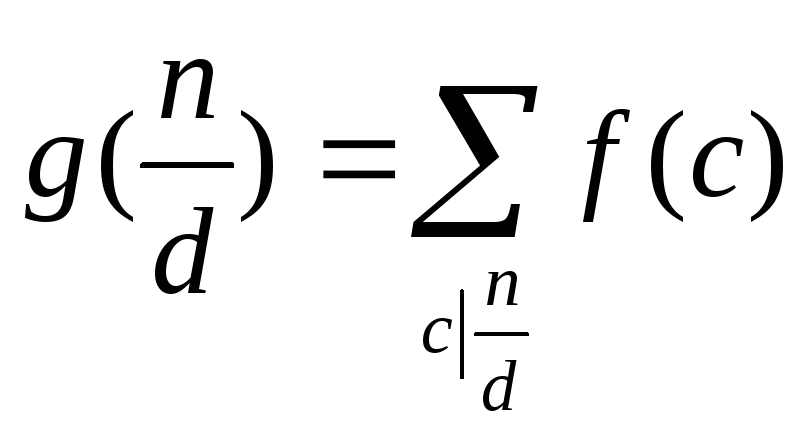
Домножим это равенство на µ(d) и просуммируем по всем d:

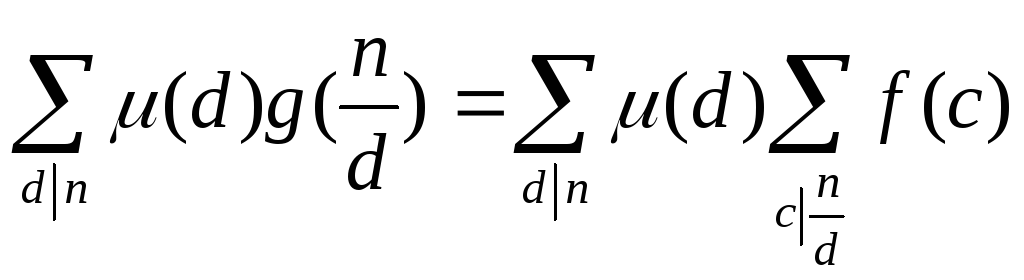
Двойная сумм справа берется по всем парам (d; c) таким, что dc делит n. Но эти пары можно перебирать в другом порядке:

Поэтому

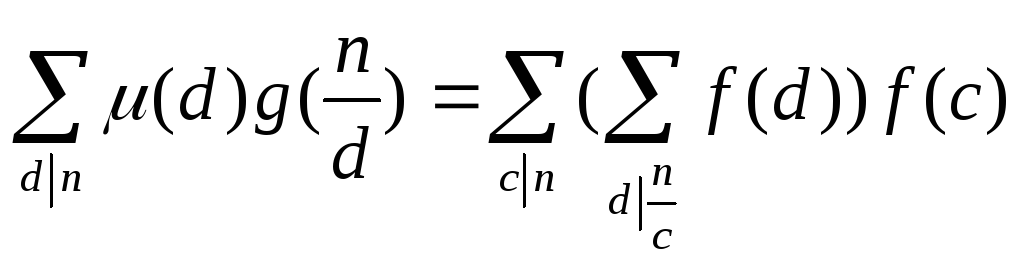
Согласно тождеству для функции Мёбиуса, сумма, взятая в скобки, ровна нулю всегда, кроме случая . Значит, внешняя сумма по переменной С состоит только из одного ненулевого слагаемого (при с = n):

■

Пример 1: Если f(n)=1, то (см. п.3)

По формуле обращения Мёбиуса:

.

Например, возьмем n = 12.

Тогда

Пример 2: Возьмем в качестве f(n) функцию Мангольд, то :

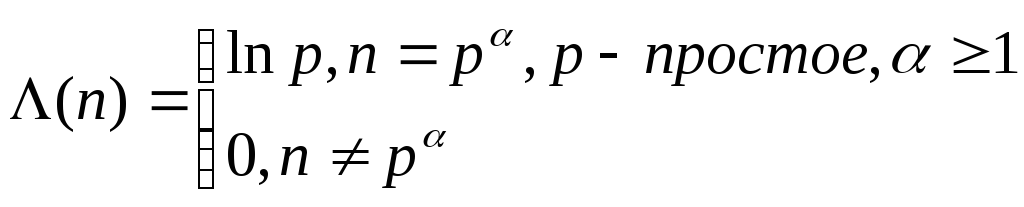
Вычислим . Пусть . Тогда (при выборе других делителей). Тогда, по определению , .

Применим закон обращения Мёбиуса:

.

Так как ln1=0, а при , то окончательно получим

.

Закон обращения Мебиуса можно обобщить.

Теорема: Пусть — некоторые натуральные числа, среди которых могут быть повторяющиеся. Пусть им соответствуют, по некоторому правилу, действительные (или комплексные) числа . Обозначим

,

Тогда .

(Суммы конечны, так как чисел и их делителей d — конечно число)

Доказательство:

■

Убедимся в том, что закон обращения Мёбиуса есть частный случай доказанной теоремы.

Пусть f(n) — произвольная функция, определенная на N.

Зафиксируем некоторое n и обозначим —

все возможные делители n. Соответствие установим по правилу:

Тогда ,

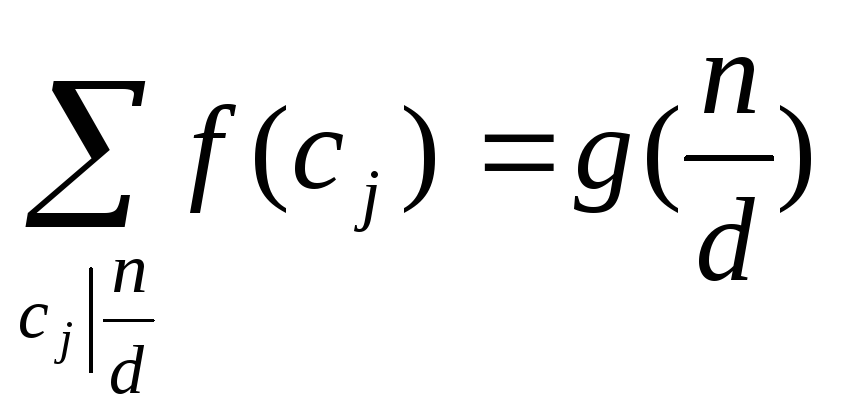|Обозначим . Тогда или, что то же самое, | = , где — функция введенная ранее.

Итак, утверждение теоремы принимает вид .

п.5 Функция Эйлера

Определение: Функция , вычисляющая количество натуральных чисел не превосходящих n и взаимно простых с n, называются функцией Эйлера.

Пример: Вычислим при . В скобках перечислены взаимно простые с n числа.

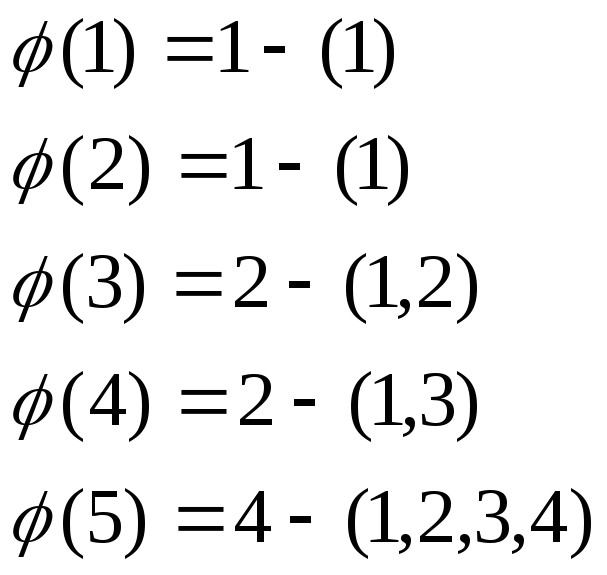
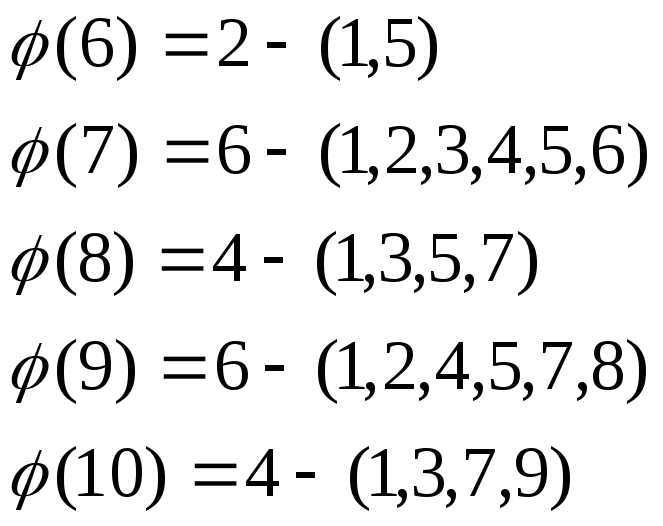
Замечание: При подсчете число 1 учитывается всегда. Число n, напротив, учитывается только при n = 1.

Отметим два важных свойства функций Эйлера:

1. Если p — простое число, то

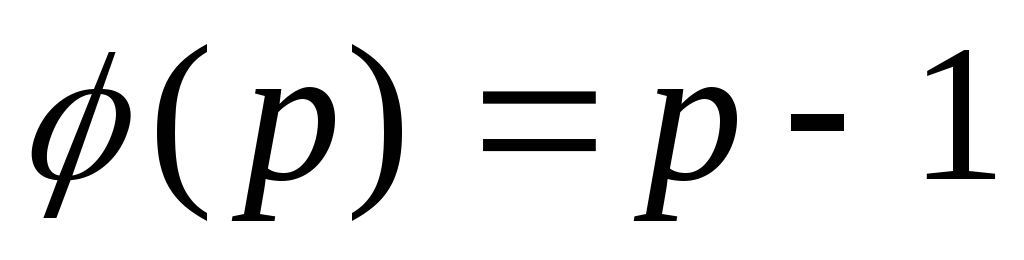
2. Если 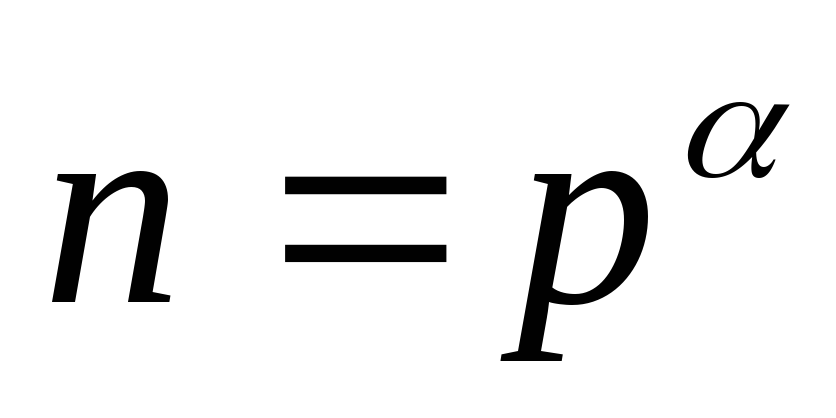, то

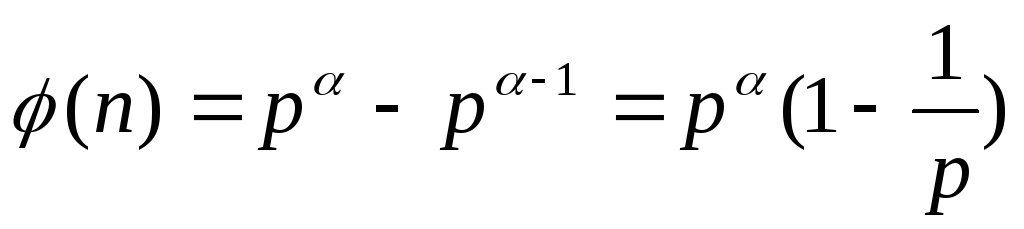
Доказательство: Свойство 1 очевидно. Для доказательства свойства 2 выпишем числа, не являющиеся взаимно простыми с . Это числа .

Всего их . Значит, остальных чисел имеется

■

Пример: .

Вычисление в остальных случаях основано на следующей теореме.

Теорема: Функция Эйлера мультипликативна.

Доказательство: Пусть a и b — взаимно простые числа. Докажем, что .

Запишем первые ab натуральных чисел в виде таблицы:

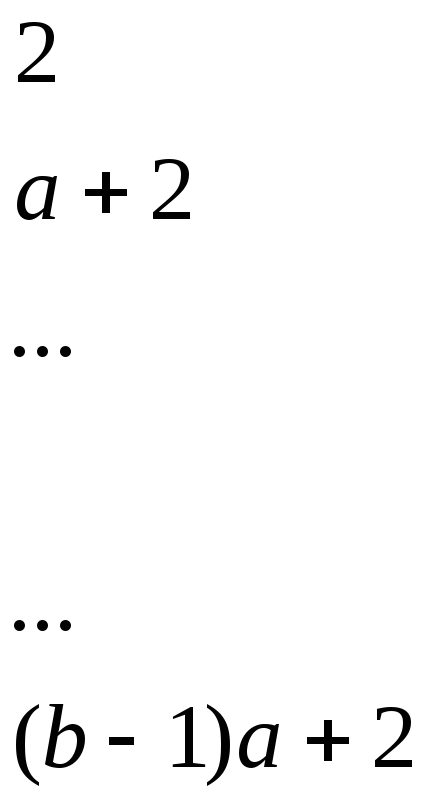
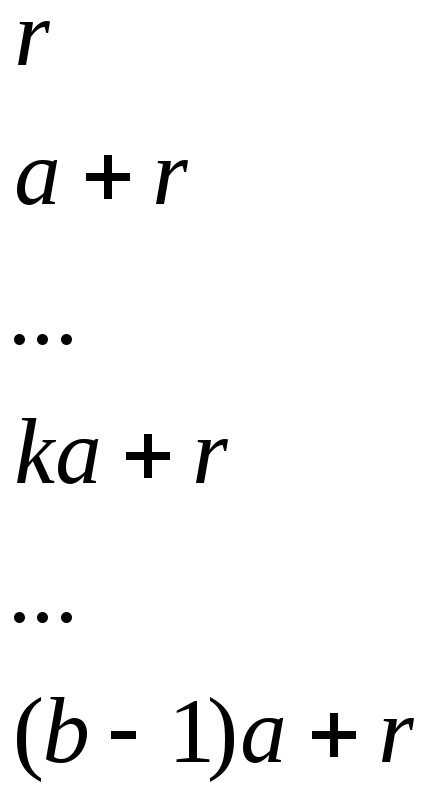
И выберем среди них числа, взаимно простые с ab.

Прежде всего отметим, что ввиду взаимной простоты a и b

.

(Это следует из того, что канонические разложения a и b состоят из различных простых множителей, при этом ни один из них не должен входить в каноническое разложение числа x). Поэтому в таблице можно сначала выбрать числа, взаимно простые с a, и уже из них выбрать взаимно простые с b.

В первой строке есть чисел, взаимно простых с a. Пусть r — одно из них. Тогда все числа вида , находящиеся в одном столбце, взаимно просты с a. Действительно, они имеют одинаковый остаток r при делении на a и то по алгоритму Евклида НОД(x,a) = НОД(a,r) = 1. Это же равенство означает, что в других столбцах (где НОД(r,a)1) нет чисел взаимно простых с a.

Рассмотрим теперь b чисел, составляющих r-й столбец:

.

Разность никаких двух чисел не делится на bу всех чисел разные остатки при делении на bэти остатки, обозначим их p, пробегают все значения 0,1,2,…,b-1. имеется ровно чисел х для которых НОД(x,b) = НОД(b,p)=1

В выбранном столбце ровно чисел взаимно простых с b.

Итак, в любом столбце содержится чисел, взаимно просты с b. Всего в таблице чисел, взаимно простых как с a, так и с b. Следовательно,

■

Следствие 1: (формула Эйлера)

Пусть .

Тогда .

Доказательство:

■

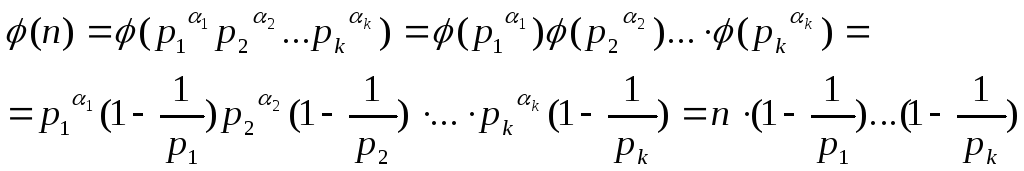
Пример:

Следствие 2:

Доказательство: Очевидно, в силу известного тождества для функции Мёбуса. (п.4)

Замечание: Другой подход к доказательству теоремы и двух ее следствий состоит в том, что следствие 2 выводится непосредственно из закона в виде следствия 1, а теорема о мультипликативности сразу же вытекает из формулы Эйлера и основной теоремы арифметики.

Приведем для сравнения, это доказательство.

Пусть . Поставим им в соответствие число .

Тогда .

В самом деле, если , то и . Из того, что d — делитель n, следует, что все значения j, кратные d, имеют вид

.

Всего их штук.

Итак, обобщим закон обращения. Мёбиуса принимает вид:

.

Просуммируем значения функции Эйлера по всем делителям числа n.

Пример: Пусть n = 20. Делители 20 это числа 1,2,4,5,10,20.

То, что полученный результат не случаен, доказал Гаусс.

Теорема: (Гаусс)

Доказательство: Воспользуемся теоремой о сумме значений мультипликативной функции по делителям число n (п.3). Пусть . Тогда Все сомножители легко вычислить, применяя формулу . Например,

Поэтому

.

■

В заключении следует упомянуть об одной нерешенной проблеме, относящейся к функции Эйлера. Верно ли, что для любого натурального n найдется другое натурально число m

такое, что . В некоторых частных случаях результат прост: если n — нечетное, то . В общем виде задача пока не ришима.