
Bilet_19
.odtСвойства
Локальные
-
Функция, непрерывная в точке
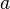 ,
является ограниченной в некоторой
окрестности этой точки.
,
является ограниченной в некоторой
окрестности этой точки. -
Если функция
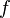 непрерывна
в точке
непрерывна
в точке 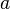 и
и 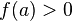 (или
(или 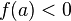 ),
то
),
то 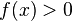 (или
(или 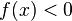 )
для всех
)
для всех 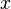 ,
достаточно близких к
,
достаточно близких к 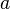 .
. -
Если функции
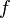 и
и 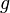 непрерывны
в точке
непрерывны
в точке 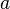 ,
то функции
,
то функции 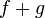 и
и 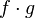 тоже
непрерывны в точке
тоже
непрерывны в точке 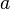 .
. -
Если функции
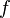 и
и 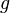 непрерывны
в точке
непрерывны
в точке 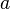 и
при этом
и
при этом 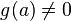 ,
то функция
,
то функция 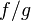 тоже
непрерывна в точке
тоже
непрерывна в точке 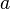 .
. -
Если функция
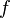 непрерывна
в точке
непрерывна
в точке 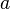 и
функция
и
функция 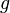 непрерывна
в точке
непрерывна
в точке 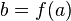 ,
то их композиция
,
то их композиция 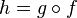 непрерывна
в точке
непрерывна
в точке 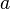 .
.
Глобальные
-
Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
-
Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
-
Областью значений функции
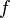 ,
непрерывной на отрезке
,
непрерывной на отрезке ![\,[a,b]](/html/25103/187/html_a3auvy4dLJ.o9u7/img-ohGVH6.png) ,
является отрезок
,
является отрезок ![\,[\min f, \ \max f],](/html/25103/187/html_a3auvy4dLJ.o9u7/img-MwJ9fg.png) где
минимум и максимум берутся по отрезку
где
минимум и максимум берутся по отрезку ![\,[a,b]](/html/25103/187/html_a3auvy4dLJ.o9u7/img-770P1V.png) .
. -
Если функция
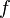 непрерывна
на отрезке
непрерывна
на отрезке ![\,[a,b]](/html/25103/187/html_a3auvy4dLJ.o9u7/img-22aIsJ.png) и
и 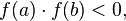 то
существует точка
то
существует точка 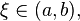 в
которой
в
которой 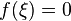 .
. -
Если функция
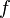 непрерывна
на отрезке
непрерывна
на отрезке ![\,[a,b]](/html/25103/187/html_a3auvy4dLJ.o9u7/img-ZE6wYs.png) и
число
и
число 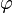 удовлетворяет
неравенству
удовлетворяет
неравенству 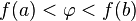 или
неравенству
или
неравенству 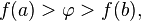 то
существует точка
то
существует точка 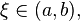 в
которой
в
которой 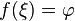 .
. -
Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
-
Монотонная функция на отрезке
![\,[a,b]](/html/25103/187/html_a3auvy4dLJ.o9u7/img-J0DFMJ.png) непрерывна
в том и только в том случае, когда область
ее значений является отрезком с
концами
непрерывна
в том и только в том случае, когда область
ее значений является отрезком с
концами 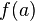 и
и 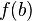 .
. -
Если функции
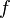 и
и 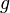 непрерывны
на отрезке
непрерывны
на отрезке ![\,[a,b]](/html/25103/187/html_a3auvy4dLJ.o9u7/img-1m2SRd.png) ,
причем
,
причем 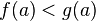 и
и 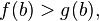 то
существует точка
то
существует точка 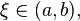 в
которой
в
которой 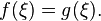 Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.
Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.
Теорема 3 (теорема о промежуточных значениях). Пусть функцияy = f(x) непрерывна на отрезке [a, b] и f(a) = A, f(b) = B. Тогда для любого числа C, заключённого между A и B, найдётся внутри этого отрезка такая точка CÎ [a, b], что f(c) = C.
Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x). Пусть f(a) = A, f(b) = B. Тогда любая прямая y = C, где C – любое число, заключённое между A и B, пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C, при котором f(c) = C.
Таким образом, непрерывная функция, переходя от одного своего значения к другому, обязательно проходит через все промежуточные значения. В частности:
Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями.
