
Bilet_12
.odtСвойства бесконечно малых
-
Сумма конечного числа бесконечно малых — бесконечно малая.
-
Произведение бесконечно малых — бесконечно малая.
-
Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
-
Если an — бесконечно малая последовательность, сохраняющая знак, то
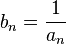 — бесконечно
большая последовательность.
— бесконечно
большая последовательность.
Сравнение бесконечно малых
Отношение
бесконечно малых величин образует
так называемую неопределённость ![]() .
.
Определения
Допустим,
у нас есть бесконечно малые при одном
и том же ![]() величины α(x) и β(x) (либо,
что не важно для определения, бесконечно
малые последовательности).
величины α(x) и β(x) (либо,
что не важно для определения, бесконечно
малые последовательности).
-
Если
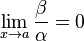 ,
то β — бесконечно
малая высшего порядка малости,
чем α. Обозначают β
= o(α).
,
то β — бесконечно
малая высшего порядка малости,
чем α. Обозначают β
= o(α). -
Если
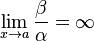 ,
то β — бесконечно
малая низшего порядка малости,
чем α. Соответственно α
= o(β).
,
то β — бесконечно
малая низшего порядка малости,
чем α. Соответственно α
= o(β). -
Если
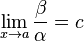 (предел
конечен и не равен 0), то α и β являются
бесконечно малыми величинами одного
порядка малости.
(предел
конечен и не равен 0), то α и β являются
бесконечно малыми величинами одного
порядка малости.
- Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).
-
Если
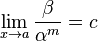 (предел
конечен и не равен 0), то бесконечно
малая величина β имеет m-й
порядок малости относительно
бесконечно малой α.
(предел
конечен и не равен 0), то бесконечно
малая величина β имеет m-й
порядок малости относительно
бесконечно малой α.
Для вычисления подобных пределов удобно использовать правило Лопиталя.
Примеры сравнения
-
При
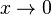 величина x5 имеет
высший порядок малости относительно x3,
так как
величина x5 имеет
высший порядок малости относительно x3,
так как 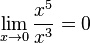 .
С другой стороны, x3 имеет
низший порядок малости относительно x5,
так как
.
С другой стороны, x3 имеет
низший порядок малости относительно x5,
так как 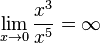 .
.
- С использованием О-символики полученные результаты могут быть записаны в следующем виде x5 = o(x3).
-
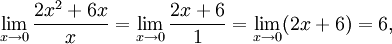 то
есть при
то
есть при 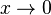 функции f(x)
= 2x2 +
6x и g(x)
= x являются
бесконечно малыми величинами одного
порядка.
функции f(x)
= 2x2 +
6x и g(x)
= x являются
бесконечно малыми величинами одного
порядка.
- В данном случае справедливы записи 2x2 + 6x = O(x) и x = O(2x2 + 6x).
-
При
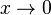 бесконечно
малая величина 2x3 имеет
третий порядок малости относительно x,
поскольку
бесконечно
малая величина 2x3 имеет
третий порядок малости относительно x,
поскольку 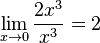 ,
бесконечно малая 0,7x2 —
второй порядок, бесконечно малая
,
бесконечно малая 0,7x2 —
второй порядок, бесконечно малая 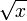 —
порядок 0,5.
—
порядок 0,5.
Эквивалентные величины
Определение
Если ![]() ,
то бесконечно малые
величины α и β называются эквивалентными (
,
то бесконечно малые
величины α и β называются эквивалентными (![]() ).
).
Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.
При ![]() справедливы
следующие соотношения эквивалентности
(как следствия из так называемых замечательных
пределов):
справедливы
следующие соотношения эквивалентности
(как следствия из так называемых замечательных
пределов):
-
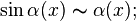
-
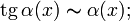
-
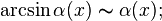
-
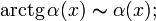
-
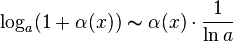 ,
где a >
0;
,
где a >
0; -
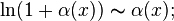
-
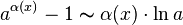 ,
где a >
0;
,
где a >
0; -
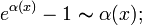
-
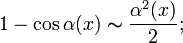
-
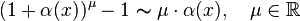 ,
поэтому используют выражение:
,
поэтому используют выражение:
-
![\sqrt[n]{1+\alpha(x)}\approx\frac{\alpha(x)}{n}+1](/html/25103/187/html_h5FvsbNfzf.ALRZ/img-DFnAcB.png) ,
где
,
где ![\alpha(x)\xrightarrow[x\to x_0]{}0](/html/25103/187/html_h5FvsbNfzf.ALRZ/img-dpMXkD.png) .
.
Теорема
- Предел частного (отношения) двух бесконечно малых величин не изменится, если одну из них (или обе) заменить эквивалентной величиной.
Данная теорема имеет прикладное значение при нахождении пределов (см. пример).
Примеры использования
-
Найти
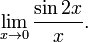
- Заменяя sin 2x эквивалентной величиной 2x, получаем
-
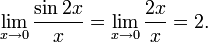
-
Найти
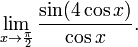
-
Так
как
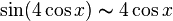 при
при 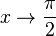 получим
получим -
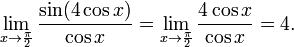
-
Вычислить .
-
Используя
формулу:
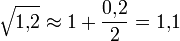 ,
тогда как, используя калькулятор (более
точные вычисления), получили:
,
тогда как, используя калькулятор (более
точные вычисления), получили: 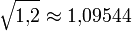 ,
таким образом ошибка составила: 0,00455,
то есть метод полезен, благодаря своей
простоте, при грубой оценке арифметических
корней близких
к единице.
,
таким образом ошибка составила: 0,00455,
то есть метод полезен, благодаря своей
простоте, при грубой оценке арифметических
корней близких
к единице.
