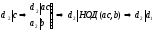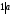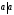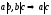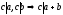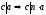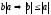Теория делимости №1
.doc§1. Теория делимости
п.1 Делимость целых чисел
Хорошо известно, что во множестве натуральных чисел
N = {1,2,3,4,5…} выполнены арифметические операции сложения и умножения.
Во множестве целых чисел Z = {0, ±1, ±2, ±3…} к ним добавляется операция вычитания. Четвертое арифметическое действие — деление (выполнимо не всегда).
Определение:
Число a
делится на число b,
если
существует такое число с,
что
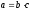 .
.
Определение:a — делимое,b — делитель,c — частное.
Обозначения: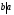 —b
делит
a(b
является делителем a)
—b
делит
a(b
является делителем a)
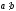 — a
кратно
— a
кратно
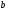 (a
делится
на
b)
(a
делится
на
b)
Пример:
12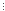 4,
4,
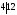 ,
27
,
27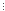 (-3)
,
(-3)
,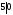 ,
но число ноль не может быть делителем
других чисел: 0 х 5.
,
но число ноль не может быть делителем
других чисел: 0 х 5.
Обозначение: n Z ={±n, ±2n,±3n,…}— множество чисел кратных n.
Теорема: (Свойства делимости)
Доказательство:
1,2
—
очевидно. 3) Если
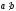 и
и
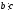 ,
то
,
то
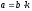 и
и
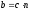 .
Тогда
.
Тогда
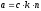 ,
т.е.
,
т.е.
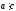 ;
4)
;
4)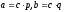 ,
значит
,
значит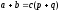 ,
т.е.
,
т.е.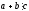 ;
;
5)
Аналогично
6)
Если
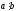 ,
то
,
то
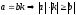 ,
т.к.
,
т.к.
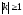
■
Замечание 1: Отношение делимости на Z рефлексивно и транзитивно (свойства 2,3) Кроме того, на N отношение делимости антисимметрично (следствие 1) .
Замечание 2: Обратное утверждение к свойствам 4 и 5 не верны. Например, 5+7 не делится на 3.
Следствие 1: Для натуральных чисел a и b:
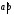 и
и
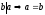
Для целых a и b:
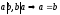 или
или
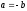
Следствие
2:
Если в равенстве
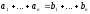 все слагаемые, кроме одного делятся на
c
,
то это слагаемое тоже делится на с.
все слагаемые, кроме одного делятся на
c
,
то это слагаемое тоже делится на с.
П.2 Деление с остатком
Целое число a не всегда можно разделить на цело на число b. Но всегда можно разделить a на b с остатком. Хорошо известен “способ деления уголком”
Пример:
4 — остаток
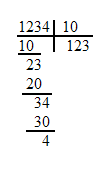
Определение:
Разделить
a
на
b
с
остатком
означает
найти два целых числа q
и
r
таких,
что
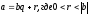
Определение: q — неполное частное; r — остаток.
Пример: Разделить -5 на 2 с остатком
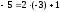 ,
остаток
всегда неотрицателен!
,
остаток
всегда неотрицателен!
Докажем,
что деление с остатком возможно для
любых целых чисел (кроме
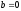 ),
притом
единственным способом.
),
притом
единственным способом.
Теорема:
Для любых целых чисел a
и
b
(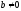 )
Существует
единственная пара чисел q
и
r
таких,
что
)
Существует
единственная пара чисел q
и
r
таких,
что
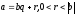
Доказательство: Докажем существование.
Пусть
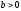 .
Рассмотрим
упорядоченные по возрастанию числа
.
Рассмотрим
упорядоченные по возрастанию числа
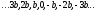
Выберем
среди них такое число bq,
что
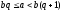 ,
обозначив
,
обозначив
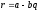 ,
получим требуемое условие
,
получим требуемое условие
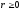 и
и
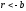 .
.
Докажем
единственность, пусть (от противного)
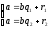
Будем
считать, что
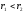 ,
тогда
,
тогда
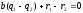
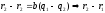
делится
на
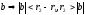 ,
что
противоречит делению остатка.
,
что
противоречит делению остатка.
■
П.3 Наибольший общий делитель. Алгоритм Евклида
Определение:
Наибольшим общим делителем (НОД)
целых чисел
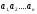 ,
называется наибольшее из положительных
чисел d
таких,
что
,
называется наибольшее из положительных
чисел d
таких,
что
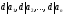
Замечание:
Пусть
d
— делитель
числа a,
тогда
d
— тоже делитель числа a.
В
дальнейшем мы будем изучать только
положительные делители т.е. в записях
вида
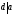 ,
подразумевать,
что
,
подразумевать,
что
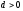 .
.
Обозначение:

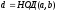 ;
Часто для упрощения записи пишут
;
Часто для упрощения записи пишут
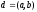
Пример: НОД(12,8) = 4; НОД(5,0)=5; НОД (0,0) не существует.
Обозначим D(a) — множество всех делителей числа a.
D(a,b) — множество всех общих делителей чисел a и b.
Эти множества конечны, поэтому найти НОД(a,b) можно перечислив все элементы множества D(a,b) и указав наибольший элемент.
Пример: Найти НОД(24;30)
Имеем
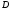 (24)
=
(24)
=
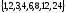
D(30)
=
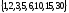
D
(24,30) =
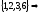 НОД
(24,30)
= 6
НОД
(24,30)
= 6
Ясно, что для больших чисел, перебор делителей неэффективен (только один поиск делителей может представлять собой трудноразрешимую задачу – см. п.2 §2) Более удобный способ вычисления НОД(a,b) был предложен еще Евклидом. Его алгоритм основан на двух простых фактах.
Лемма
1:
Если
 ,
то
,
то
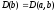 .
В частности, совпадают наибольшие
элементы этих множеств: b=НОД(a,b)
.
В частности, совпадают наибольшие
элементы этих множеств: b=НОД(a,b)
Доказательство:
Любой
общий делитель чисел a
и b
является
делителем b,
значит,
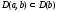 .
С другой стороны, любой делитель числа
b
по
свойству
3
п.1 является также делителем a
и, значит, общим делителем двух чисел
.
С другой стороны, любой делитель числа
b
по
свойству
3
п.1 является также делителем a
и, значит, общим делителем двух чисел
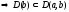 .
.
Два условия обеспечивают равенство множеств D(b)=D(b,q), а так как множества конечны, то их наибольшие элементы равны.
■
Лемма
2:
Если
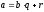 ,
то D(a,b)=D(b,r).В
частности, НОД(a,b)=НОД(b,r)
,
то D(a,b)=D(b,r).В
частности, НОД(a,b)=НОД(b,r)
Доказательство:
Пусть
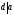 и
и
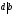 .
Тогда по свойствам делимости
.
Тогда по свойствам делимости
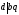 и
и
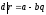 .
Итак,
общий делитель a
и
b
является
общим делителем b
и
r,
т.е.
.
Итак,
общий делитель a
и
b
является
общим делителем b
и
r,
т.е.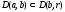 .
Обратно, если
d(r
и d)b,
то
по свойствам делимости
.
Обратно, если
d(r
и d)b,
то
по свойствам делимости
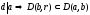 .
.
Доказано
равенство двух множеств:
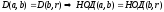
■
Алгоритм
Евклида состоит в следующем. Пусть даны
два числа a
и
b,
будем считать, что
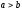 ,
разделим a
на
b
с
остатком:
,
разделим a
на
b
с
остатком:
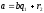 ,
далее разделим на
,
далее разделим на
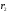 :
:
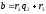 .
.
Затем
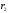 делим на
делим на
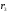 ,
,
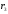 на
на
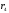 ,
и так до тех пор, пока остаток не станет
равен нулю. С каждым следующим делением
остаток уменьшается,
,
и так до тех пор, пока остаток не станет
равен нулю. С каждым следующим делением
остаток уменьшается,
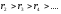 поэтому
процесс остановится через конечное
число шагов
поэтому
процесс остановится через конечное
число шагов
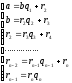
Теорема:
Последний
ненулевой остаток
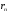 равен наибольшему общему делителю чисел
a
и
b;
равен наибольшему общему делителю чисел
a
и
b;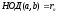 :
:
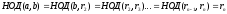
Пример:
Найти
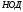 (525,231)
(525,231)
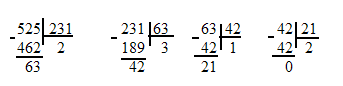
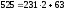
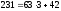
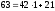
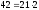
Ответ: НОД(525,231)=21
Замечание:
Если
обозначить
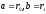 то
краткая запись Евклида такова:
то
краткая запись Евклида такова:
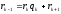 ,
(k=1,2,…
,
(k=1,2,… )
)
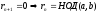
Геометрический смысл алгоритма Евклида:
Отрезок
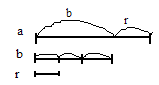
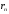 является
общей мерой отрезков a
и
b,
т.е.
данные отрезки можно разбить на целое
число частей длины
является
общей мерой отрезков a
и
b,
т.е.
данные отрезки можно разбить на целое
число частей длины
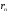
Свойства
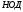
1°
Множество общих делителей чисел a
и
b
совпадает
с множеством делителей числа
 .
.
Доказательство
следует
из леммы 2 и алгоритма Евклида:
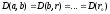
2° Общий множитель можно вынести за знак НОД:
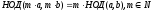
Доказательство:
Все
равенства в алгоритме Евклида можно
домножать на m.
Получим
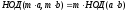 .
.
■
3°
Если
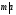 и
и
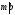 ,
то
,
то
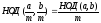 .
.
Доказательство: По предыдущему свойству:
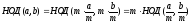
■
4°
Пусть d=НОД(a,b),
тогда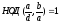
Свойство
4° есть частный случай свойства 3°. По
сути, свойство 4° означает, что любую
дробь
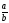 можно сократить на число d.
после чего дробь (
можно сократить на число d.
после чего дробь (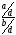 ) станет несократимой. Если заданы
несколько чисел
) станет несократимой. Если заданы
несколько чисел
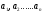 ,
то их НОД
выполняется пошагово, вычислим
последовательно.
,
то их НОД
выполняется пошагово, вычислим
последовательно.
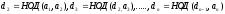
По
свойству 1° множество
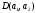 всех общих делителей
всех общих делителей
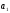 и
и
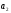 совпадают с множеством
совпадают с множеством
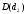 делителей их НОД.
Аналогично,
делителей их НОД.
Аналогично,
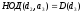 и т.д. Поэтому
и т.д. Поэтому
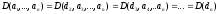 .
.
Но равенство конечных множеств означает равенство их наибольших элементов.
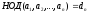
Пример: Найти НОД(6,10,15,24) = d
Имеем,
НОД(6,10)=2
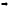 d
= НОД(2,15,24)
далее,
d
= НОД(2,15,24)
далее,
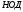 (2,15)=1
(2,15)=1
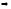 d=
НОД(1,24)
d=
НОД(1,24)
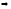 d
=1
d
=1
п.4 Взаимно простые числа
Определение: Числа a и b называются взаимно простыми если их НОД(a,b)=1
Пример:
НОД(14,15)
=1
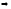 Числа
14 и 15 взаимно простые.
Числа
14 и 15 взаимно простые.
Определение:
Числа
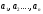 называются взаимно
простыми,
если
называются взаимно
простыми,
если
НОД(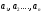 )
=1
)
=1
Определение:
Числа
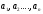 называются
попарно
простыми,
если
называются
попарно
простыми,
если
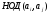 при
при
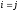 .
.
Если числа попарно взаимно просты, то они взаимно просты. Обратное неверно.
Пример: НОД(6,10,15,24)= 1, т.е. четыре числа взаимно. Но попарно они не будут взаимно простыми. Например, НОД (6,10) = 2, НОД(6,15) = 3, НОД(6,24) = 6.
Свойства взаимно простых чисел
1°
Пусть d=НОД(a,b).
Тогда
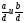 - взаимно простые числа.
- взаимно простые числа.
Это другая формулировка свойства 4 НОД .
2°
Если ab
делится на c
и
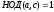 ,
то b
делиться на c.
,
то b
делиться на c.
Доказательство:
так
как ab
и
ac
делятся
на c,
то
по свойству 1 их наибольший общий делитель
делится на
 .
Но
НОД(ab,ac)=b.
НОД(a,c)
.
Но
НОД(ab,ac)=b.
НОД(a,c)
Следовательно, b делится на c.
■
3°
Пусть
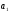 и
и
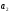 взаимно просты. Тогда
b
делиться на
взаимно просты. Тогда
b
делиться на
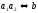 делиться на
делиться на
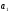 и b
делиться
на
и b
делиться
на
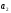 .
.
Доказательство:
“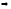 ”
делится на
”
делится на
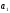
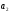 .
Произведение
.
Произведение
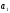
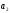 делится на
делится на
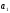 и на, значит, по транзитивности (третье
свойство делимости) b
делится на
и на, значит, по транзитивности (третье
свойство делимости) b
делится на
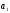 и на
и на
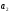
“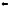 ”
Пусть
b
делится
на
”
Пусть
b
делится
на
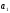 и
на
и
на
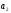 .
Тогда
.
Тогда
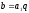 .
Делимость
на
.
Делимость
на
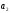 означает (свойство 2), что q
делится на
означает (свойство 2), что q
делится на
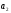 т.е.
т.е.
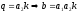 ,
т.е b
делиться
на
,
т.е b
делиться
на


Замечание: Простым следствием этого свойства служат некоторые признаки делимости, например, 864 делиться на 6, т.к. оно делиться на 2 и на 3.
4°
Пусть a
и
b
взаимно
просты. Тогда
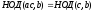
Доказательство:
Обозначим
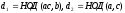
1)