Числовые сравнения №1

§5 Числовые сравнения

п.1 Определение и основные свойства сравнений

Пусть — произвольное натуральное число. Будем называть его модулем.

Определение: Целые числа a и b сравнимы по модулю m, если их разность a-b делятся на m.

Обозначение: a ≡ b (mod m).

Пример:

17 ≡ 5 (mod 17), 19 ≡ -1 (mod 10)

15 ≡ 0 (mod 5), 11≡ 1 (mod 5)

Замечание: Сравнение 17 ≡ 5 (mod 12) иллюстрирует хорошо знакомую ситуацию. По модулю 12 мы обычно называем время, говоря "сейчас 5 часов", вместо "сейчас 17 часов".

Теорема 1: Следующее утверждения для целых чисел a и b равносильны:

1. разность a-b делится на m.

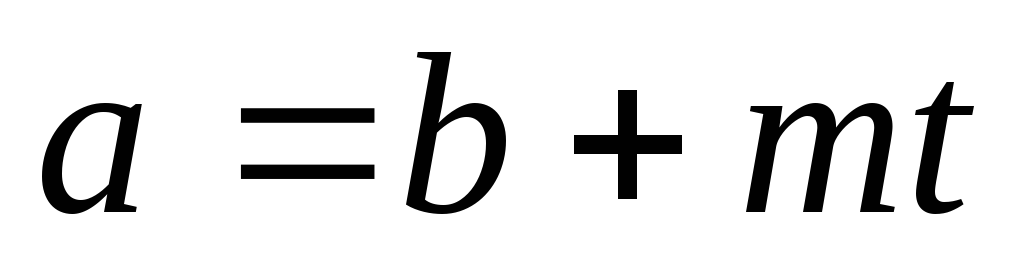2. , где .

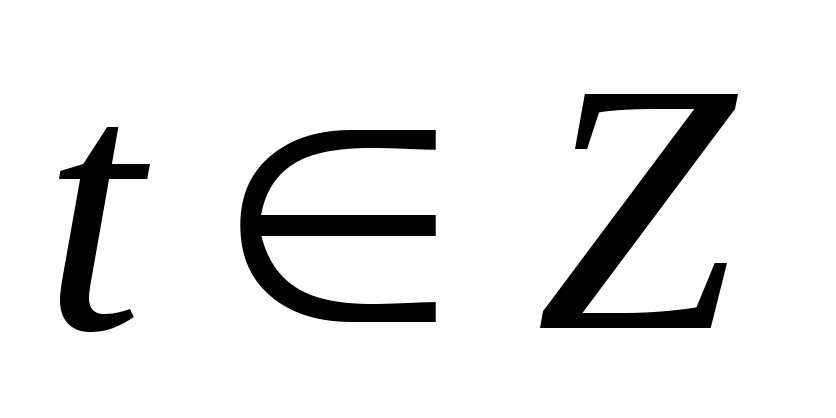3. a и b имеют одинаковые остатки при делении на m.

Доказательство: 1)2) Пусть a-b делятся на m. Тогда a-b=mt

или .

2)3) Пусть , и пусть b при делении на m имеет остаток r, т.е. 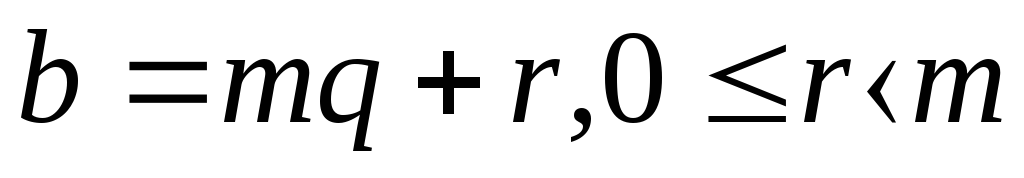. Тогда , где 0 ≤ r < m.

Следовательно r — остаток от деления a на m. Значит, a и b имеют равные остатки от деления на m.

3)1) Пусть Тогда делится на m.

Доказанная теорема означает, что любое из трех равносильных утверждений можно принять за определение сравнения.

Перейдем к изучению свойств сравнений. Отношение сравнимости двух целых чисел является примером бинарного отношения на множестве Z. Во многом это отношение похоже на отношение равенства. Свойства 1°—4° иллюстрируют это сходство.

1°. Отношение сравнения является отношением эквивалентности:

1. a ≡ a (mod m)

2. a ≡ b (mod m) b ≡ a (mod m)

3. a ≡ b (mod m), b ≡ c (mod m) a ≡ c (mod m)

Доказательство:

1. Рефлексивно очевидна, т.к. a-a делиться на m.

2. Симметричность не менее ясна: если a-b делиться на m, то

b- a тоже делится на m.

3. Транзитивность следует из равенства и свойств делимости.

■

2°. Сравнения по одному и тому же модулю можно складывать, вычитать и умножать:

если a ≡ b (mod m), c ≡ d (mod m), то

a + c =b + d (mod m)

a - c =b – d (mod m)

a · c =b · d (mod m)

Доказательство: Пусть , , где и — целые. Тогда

что по теореме 1 равносильно требуемым сравнениям.

■

Пример:

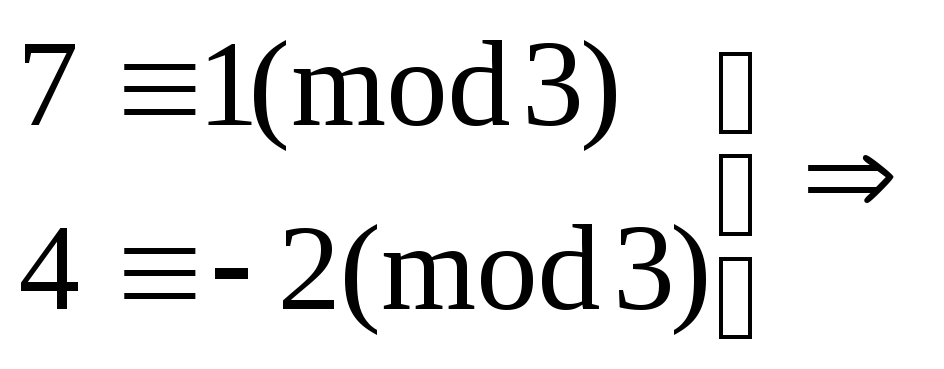
3°. Обе части сравнения можно увеличить на одно и тоже число, домножать на одинаковый множитель или возвести в одинаковую степень:

если a ≡ b (mod m), то

a + k ≡ b + k (mod m), kZ,

a · k ≡b · k (mod m), kZ,

(mod m), kN.

Доказательство: Требуемые утверждения легко получить, применяя свойство 2° к сравнениям a ≡ b (mod m) и

k ≡ k (mod m).

■

Пример: 9 ≡ 4 (mod 5). Для k = 2 получим верные сравнения:

11 ≡ 6 (mod 5), 18 ≡ 8 (mod 5), 81 ≡ 16 (mod 5).

4°. Члены сравнения можно переносить из одной части в другую с переменой знака:

a + b ≡ с (mod m) a ≡ c-b (mod m)

Доказательство: Следует из свойства 3° при k = -b.

■

Следующие два свойства показывают отличие числовых сравнений от обычных равенств.

5°. В любой части сравнения можно добавить или отбросить слагаемое, кратное модулю:

a ≡ b (mod m) a + m · k ≡ b (mod m)

Доказательство: По определению сравнимости:

m · k ≡ 0 (mod m). Складывая это сравнение с данным сравнением

a ≡ b (mod m) получим требуемое. Для доказательства обратного утверждения используем операцию вычитания.

■

Пример: Свойство 5° используют при подсчете дней недели:

3 ≡ b (mod 7) 24 ≡ b (mod 7).

Если 3 числа были вторник, то 24 числа тоже будет вторник.

6°. Обе части сравнения можно сократить на их общий множитель, если он взаимно прост с m:

если a · k ≡ b · k (mod m) и при этом НОД(k,m) = 1,

то a ≡ b (mod m).

Доказательство: Пусть a · k - b · k делится на m. По условию

k и m взаимно простые a-b делиться на m a ≡ b (mod m).

■

Замечание: Условие взаимной простоты k и m очень важно. Вообще говоря, сокращение может привести к неверному результату. Например, 8 ≡ 6 (mod 2), но 4 3 (mod 2). Впрочем, иногда после сокращения на k результат может оказаться верным, хотя k и m не взаимно просты:

Например, 85 ≡ 10 (mod 15).

После сокращения на 5 получим верное сравнение

17 ≡ 2 (mod 15).

Рассмотренные свойства сравнений обобщаются следующее теоремой.

Теорема 2: Пусть — с целыми коэффициентами. Пусть x ≡ y (mod m).

Тогда p(x) ≡ p(y) (mod m).

Если, кроме того, (mod m), i = 0,1,2…n, то

(mod m).

Доказательство: Непосредственно следует из свойств 2° и 3°.

Замечание 1: Аналогичная теорема верна и для многочленов от n переменных с целыми коэффициентами. Например,

если (mod m), i =1,2,3…n, то

(mod m).

Замечание 2: Встречающиеся в сравнении показатели степеней, нельзя заменять сравнимыми по модулю m. Иначе говоря, из того, что n ≡ k (mod m) не следует, что

(mod m). Например, 3 ≡ 8 (mod 5), но (mod 5), так как (mod 5), а (mod 5).

В свойствах 7° — 10° некоторые манипуляции проводят не только с обеими частями сравнения, но и с модулем m.

7°. Обе части сравнения и модуль можно домножить или сократить на их общий множитель:

a ≡ b (mod m) a · k ≡ b · k (mod mk)

Доказательство: Пусть a ≡ b (mod m). Тогда a = b + m∙t a∙k = b∙k + m∙k∙t a∙k ≡ b∙k (mod mk).

Эти же рассуждения можно провести в обратном порядке.

■

8°. Если два числа сравнимы по модулю m, то они сравнимы по любому модулю d, делителю числа m:

.

Доказательство: Если a-b делиться на m, а m делиться на d, то по транзитивности a-b делиться d a ≡ b (mod d).

■

9°. Если два числа сравнимы по нескольким модулям, то они сравнимы по модулю, равному наименьшему общему кратному этих модулей:

,

где .

Доказательство: Если , то разность a-b делиться на и на . Значит, (свойство 1 НОК) a-b делиться на , т.е. a ≡ b (mod m). Такое же рассуждение сохраняет силу и для нескольких модулей.

■

10°. Если a ≡ b (mod m), то множество общих делителей a и m совпадает с множеством общих делителей b и m. В частности НОД(a,m) = НОД(b,m).

Доказательство: Пусть a ≡ b (mod m). Тогда a – b = m∙t.Если d — общий делитель a и m, то — общий делитель b и m. Обратное аналогично.

■

п.2 Простейшие применения сравнений

Теория сравнений дает в руки исследователя очень эффективный инструмент для решения теоретико − числовых задач. Проиллюстрируем его действенность несколькими элементарными примерами.

Пример 1: Найти остаток от деления на 7.

Решение: Имеем сравнение 2012 ≡ 612 ≡ -18 ≡ 3 (mod 7). Значит,

(mod 7)

Но , поэтому

Ответ: остаток равен 3.

Пример 2: Доказать, что делится на 17 при всех .

Решение: Воспользуемся тем, что 258 (mod 17). Имеем

Следовательно, данная сумма делится на 17.

Пример 3: Вывести признаки делимости на 9 и на 11.

Решение: Любое натурально число N можно записать в виде

Заметим, что 10 ≡ 1 (mod 9). Следовательно,

Число сравнимы по модулю 9, значит они имеют одинаковые остатки при делении на 9. В частности,

|| N делится на 9 сумма цифр числа N делится на 9||

Аналогично, из сравнения 10 ≡ -1 (mod 11) следует, что

Отсюда следует, что

N делится на 11Разность между суммой цифр числа N, стоящих на нечетных местах и суммой цифр, стоящих на четных местах, делится на 11.

Пример 4: Доказать, что уравнение не имеет решений в целых числах.

Решение: Любое решение x должно удовлетворять сравнению

При делении на 5 число x может иметь в остатке 0,1,2,3 и 4.

Но, так как

значит не может иметь остаток 3, т.е. сравнение не имеет решений.

Пример 5: Определить день недели по заданной дате.

Решение: Пусть N обозначает год, m — месяц, d — день

(1≤ m≤12), (1≤ d≤31) Первым месяцем года (m = 1) будем считать март, вторым (m =2) — апрель и т.д. Тогда в високосные годы день 29 февраля добавляется в конце года, что удобно для расчета.

Обозначим ω — номер для недели (1≤ ω≤ 7), начиная отсчет с понедельника:

ω = 1 — Пн, ω = 2 — Вт, ω = 3 — Ср ,…, ω=7 —Вс.

Пусть — номер того дня недели, который мы примем за точку отсчета. Напомним, что Россия перешла на григорианский календарь в феврале 1918 года, поэтому примем в качестве день недели 1 марта 1920 года. Таким образом, считаем

N ≥ 1920.

Пусть — номер дня 1 марта N-го года. Заметим, что

365 ≡ 1 (mod 7), поэтому каждый невисокосный год номер дня недели увеличивается на 1. Если же прошлый год был високосным, то к номеру дня недели добавим 2, т.к.

366 ≡ 2 (mod 7). Следовательно,

(mod 7)

Упростив это выражение, получим

(mod 7),

(mod 7).

Вычислим . 1 марта 2012 года приходится на четверг, т.е. отсюда следует, что

(mod 7),

(mod 7).

Итак, 1 марта 1920 года был понедельник, следовательно,

(mod 7). (1)

Пусть теперь задано число d месяца m года N. Чтобы определить искомый день недели осталось вычислить количество дней, прошедших от 1 марта до заданной даты. Вычислим сначала номер дней недели для 1 числа каждого месяца.

В марте 31 день 1 апреля имеет номер (mod 7)

В апреле 30 дней 1 мая имеет номер (mod 7)

и так далее, составим небольшую таблицу, в которой указано то слагаемое, которое нужно прибавит к .

Номер возрастает примерно на в месяц. Поэтому нетрудно подобрать формулу

m = 1,2,3…,12

которая дает нужное добавочное слагаемое для любого месяца.

Итак, если ω — искомый день недели d числа m месяца N года, то к формуле (1) нужно прибавить и (d-1) — количество дней от 1 числа до нужной даты. В итоге получим

(mod 7)

Определим, для примера день недели 22 июня 1941 года. Имеем N = 1941, m = 4, d = 22.

Итак, 22 июня 1941 года было воскресенье.