Теория делимости №2

5◦. Пусть каждое из чисел взаимно просто с b, тогда их произведение взаимно просто с b.

Доказательство: По свойству 4.

6◦. Если каждое из чисел взаимно просто каждым из , то произведение и также взаимно просты.

Доказательство: По свойству 5 имеем

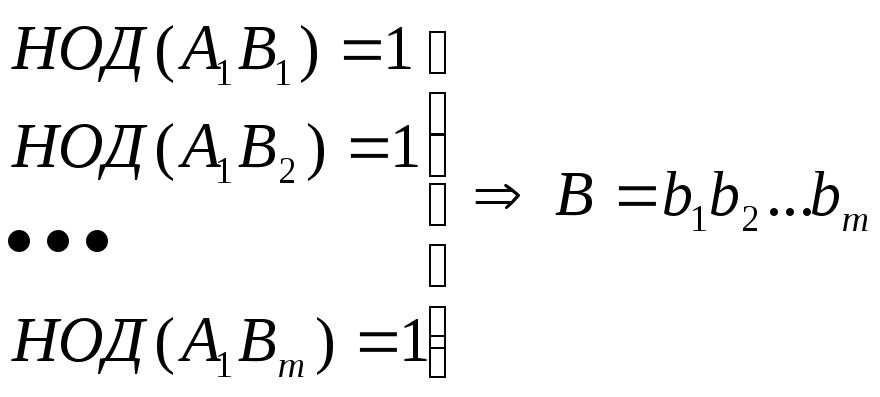взаимно просто с А.

Следствие. Если числа a и b взаимно простые, то любые их натуральные степени и также взаимно простые.

Полученное следствие применяется при доказательстве иррациональности некоторых чисел.

Утверждение. Пусть c не является n-ой степенью целого числа

Тогда - иррациональное число.

Доказательство: Пусть - несократимая дробь со знаменателям

Тогда , значит дробь также, несократима. В частности, и значит, при число не является рациональным.

Пример. — Иррациональное число, т.к. ни при каких целых х.

п.5 Наименьшее общее кратное

Определение. Наименьшим общим кратным (НОК) чисел называется наименьшее из положительных чисел k таких, что

Замечание. Пусть k — кратное числа а. Тогда (–k) тоже кратное а. В дальнейшем мы будем рассматривать только положительное кратное, т.е. в записи a|k подразумеваем, что k>0.

Обозначение. или

Часто для упрощения записи пишут

Примеры:

НОК(12, 8)=24

НОК(1, c)=c

НОК(12, -8)=24

НОК(0, c)—не сущ.

Докажем, что вычисление НОК двух чисел сводится к вычислению их НОД.

Теорема. a,b — натуральные числа

Доказательство. Обозначим . Тогда , где .

Пусть М — произвольное общее кратное чисел a и b (a|M, b|M).

Покажем, что М можно записать в виде, где

Действительно, М кратно а, значит М = аq. Далее, М = аq делится на — целое число.

Ввиду взаимной простоты и получим, что q делится на , т.е.

. Обратно, если М имеет вид , то он делится на а и на b.

Таким образом, образом получена общая формула для всех чисел, кратных a и b.

Наименьшие из этих чисел получится при

■

Пример.

Свойства НОК.

1◦. Множество общих кратных чисел a и b совпадает с множеством кратных числа НОК(a,b).

Доказательство. Следует из формулы ,

. М — произвольное общее кратное a и b.

2◦. Общий множитель можно выносить за знак НОК

.

Доказательство.

■

3◦. Если a|m и b|m, то

Доказательство аналогично свойству 3 для НОД.

4◦.Если a и b взаимно простые, то НОК(а,b) = ab.

Доказательство. Очевидно.

Пример.

Пусть заданно несколько чисел: . Алгоритм вычисления их НОК, аналогичен алгоритму поиска НОД нескольких чисел.

Вычислим последовательно:

Полученное на последнем шагу число m является наименьшим общим кратным исходных чисел

Действительно, согласно свойству 1.

. Где — множество всех общих кратных упомянутых чисел.

Следовательно, наименьший элемент множества совпадает с наименьшим элементом , т.е. с числом .

Пример. Найти НОК(6,10,15,24) = х.

Имеем

Замечание: Если попарно взаимно простые, то Пример.

п.6. Линейная форма НОД.

Теорема. Если d=НОД(a,b), то существуют целые числа u и v такие, что au+bv = d

Определение. Выражение au+bv называют линейной формой числа d.

Доказательство. Воспользуемся алгоритмом Евклида.

Выразим из предпоследнего равенства

Подставим в это равенство .

Получим , где , .

Поднимаясь по алгоритму Евклида снизу вверх и выражая остатки получим в итоге равенство с целыми коэффициентами u и v.

■

Смысл описанных действий легко понять на конкретном примере.

Пример. Записать НОД(90,35) в виде линейной формы

Решение. Первым делом вычислим НОД

Теперь выразим число 5 через исходное число:

Итак, u=2, v=–5

Следствие. (Критерий взаимной простоты)

Числа a и b взаимно простые тогда и только тогда когда существуют целые числа u и v такие, что au+bv=1

Доказательство.“” сразу следует из теоремы 1.

“” Пусть d=НОД(a,b). Левая часть равенства au+bv=1 делится на d, значит 1 — делится на d, т.е. d=1.

Теорема 2. НОД(a,b) если наименьшее положительное число среди чисел, которые можно записать в виде au+bv, .

Доказательство. Пусть S — положительных целых чисел вида au+bv. Пусть d — наименьший элемент множество S. , поэтому . Разделим a на d с остатком:

.

Выразим от сюда r:

Это означает, что или r = 0. Но d — наименьший элемент S, остаток . Следовательно, r = 0, т.е. d|а.

Аналогично d|b.

Осталось заметить, что любой общий делитель чисел a и b (по свойству делимости) делит также число .

Следовательно, d = НОД(a,b)

■

Замечание: Теорема 2 хоть и содержит более сильное утверждение, чем теорема 1, но не дает алгоритма, представляющего НОД(a,b) в виде линейной формы.

п.7 Линейные диофантовы уравнения.

Решение уравнений в целых числах — это одна из древнейших математических задач. Древнегреческий математик Диофант умел решать отдельные уравнения, содержащие неизвестные величины в 3-й и даже в 4-й степени. Мы пока ограничимся линейными уравнениями с двумя неизвестными.

Определение Уравнение ax+by=c, где , решение которого x, y есть целые числа, называется диофантовым уравнением первой степени.

Пример.90x + 35y = 5

Легко проверить подстановкой, что любая пара чисел

x=2+7t, y = –5–18t, является решением данного уравнения.

Пример. Уравнение 2x – 6y = 3 не имеет решений, т.к. левая часть уравнения делится на 2 (четная), а правая часть — нет (нечетная).

Теорема 1. Уравнение ax – by = c разрешимо в целых числах тогда и только тогда когда с делится на НОД(a,b)

Доказательство. Обозначим d = НОД(a,b)

“” Пусть существуют x и y такие, что c = ax + by.

d|a, d|b по свойствам делимости d|c.

“” Пусть d|c, т.е. c = dk

По теореме 1 п.6 существуют целые u и v такие, что d = au + bv

Следовательно, , т.е. пара чисел (uk, vk) задает решение уравнения ax + by = c

■

Следствие. Если с делится на НОД(a,b), то пара чисел

Где u, v — коэффициенты линейной формы au + by = d, является решением

Уравнения ax + by = c.

Пример. Найти частное решение уравнения

Решение.

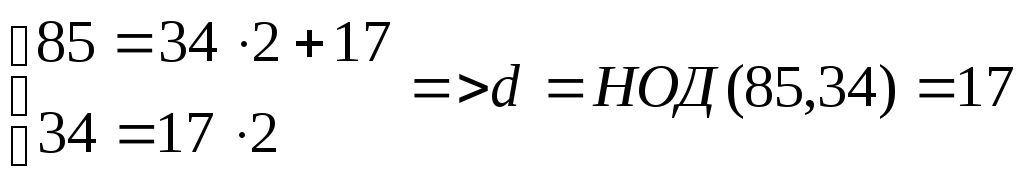
Находим, что , т.е. u = 1, v = – 2

Следовательно,

Проверка:

Заметим, что исходное уравнение можно сократить на 17 (любое разрешимое уравнение сократимо на d). Получим уравнение 5x + 2y = 3 для которого легко подобрать другое частное решение x = 1, y = – 1.

В следующей теореме докажем, что линейное диофантово уравнение разрешимо, то оно имеет бесконечное число решений, а также выведем общую формулу, задающую все его решения.

Теорема. Если известно частное решение (х, у) уравнение , то общее решение этого уравнения можно записать в виде , где d = НОД(a,b)

Доказательство. Отметим сначала, что числа а, значит и х, у – целые.

Прежде всего, заметим, что

Т.е. пара (х, у) удовлетворяет уравнению р и любых целых t.

Докажем, что других решений уравнение ax + by = c не имеет.

Пусть (х, у) – некоторое решение, отличное от

Тогда

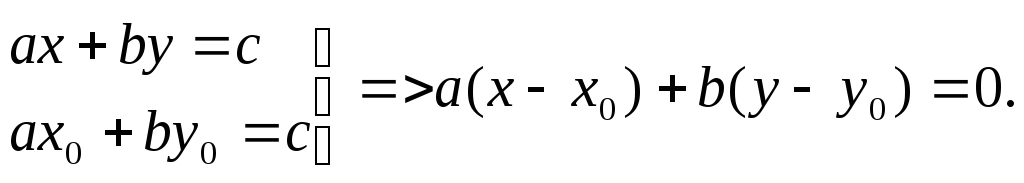
Разделим на d:

Значит, делится на . Но числа взаимно простые, следовательно, делится на , т.е. . Отсюда

■

Пример. Решить уравнение 85х + 34у = 51

Выше найдена . Общее решение имеет вид: