Простые числа №2

Ослабим требования к функции f(x). Пусть среди её значений будут как простые, так и составные, но простых значений будет бесконечно много. Например, среди чисел вида нередко встречаются простые числа:

2,5,17,37,101,197,257,…

Но гипотеза о том, что их бесконечно много это одна из нерешенных проблем.

Очень мало известно о представлении простых чисел другими функциями. Наверняка установлено лишь то, что среди арифметических прогрессий a+bx с взаимно простыми a и b содержится бесконечно много простых чисел (теорема Дирихле, 1837).

Ситуация меняется, если воспользоваться функциями нескольких переменных. Дирихле доказал, что любая квадратичная форма , в которой коэффициенты

a, b, c взаимно просты генерирует бесконечное множество простых чисел. Более того, из результатов Матиясевича (о том, что диофантовесть множества равносильна его перечислимости) следует существование многочлена, множество положительных значений которого совпадает с множеством простых чисел. Пример такого многочлена 6ой степени от 26 переменных можно найти в [-].

п.4 Основная теорема арифметики

Легко доказать, что любое натурально число раскладывается на простые множители, например, . Нельзя ли получить тот же результат, перемножая другие простые числа? Докажем, что это невозможно. Например, в равенстве

Совсем неочевидно, что сомножители являются составными числами, тем не менее, этот факт вытекает из следующей теоремы.

Теорема: (Основная теорема арифметики)

Любое натуральное число либо является простым, либо его можно записать в виде произведения простых чисел

причем единственным образом, с точностью до порядка сомножителей.

Замечание: и считаются одним и тем же разложением числа 30.

Доказательство: 1) Существование разложения на множители.

Пусть — наименьший простой делитель a. Тогда .

Если и — наименьший простой делитель , то и, значит, . Аналогично получим и так далее. Поскольку через конечное число шагов получим и .

2) Единственность разложения.

Предположим, что а можно разложить на множители двумя способами:

a делится на делится на . Тогда (§2 п.1 свойство 4 + замечание) один из множителей, например делится на . Но простое . Сократим равенство на :

и повторим рассуждение. Получим и так далее.

Если , то, сократив все одинаковые множители, получим противоречивое равенство .

Итак, произведения состоят из одинакового числа равных сомножителей, т.е. разложение а единственно.

■

Простые множители в разложении числа а могут повторяться. Пусть множитель встречаются раз. Запишем такие произведения в виде степеней и расположим все по возрастанию.

Определение: , (*)

(*) — каноническое разложение числа а на множители.

Пример:

Замечание 1: Сравним формулу (*) с разложением вектора по базису: . Простые числа образуют мультипликативный базис во множестве N (— коэффициенты разложения), чем объясняется их особая роль при изучении свойств натурального ряда.

Замечание 2: Число 1 не относится к простым прежде всего потому, что иначе нарушится единственность разложения на множители ()

Замечание 3: Рациональные дроби тоже однозначно записываются в каноническом виде, если допустить отрицательные значения . Например, .

Следствие 1: Если , то любой делитель а имеет вид , где ( i = 1,…k)

Доказательство: Очевидно, любое число d указанного вида делит а. Обратно, пусть . Тогда . Следовательно все простые делители числа d входят в разложение а со степенями .

■

Следствие 2: Пусть , .

Здесь — простые числа, которые входят в разложение хотя бы одного из чисел a и b. Некоторые из показателей

и могут быть равны нулю. Пусть , . Тогда , .

Доказательство: Пусть . Очевидно, и .

Пусть — другой общий делитель a и b. По следствию 1 , где и . Отсюда следует, что . Для НОК доказательство аналогично.

■

Пример: Найти НОД и НОК чисел а = 1008 и b=1080

Имеем . Тогда .

Замечание: Из следствия 2 сразу же выводится формула .

При всей кажущейся очевидности основной теоремы арифметики ее нельзя произвольно переносить на другие числовые системы.

Пример: Коротка арифметика Гильберта — множества вида :

= {1,5,9,13,17,21,…}

с одной операцией умножения, относительно которой множество замкнуто .

Числа являются составными, а, например, 9 или 21 — простыми в .

В этой арифметике число 693 раскладываются на простые множители неоднозначно:

п5. Число делителей и сумма делителей

Основная теорема арифметики позволяет дать ответ на некоторые вопросы о натуральном числе а. Так, следствие 1 указывает, какие числа является делителями а. Нетрудно подсчитать сколько всего делителей имеет натуральное число а, а также найти их сумму.

Обозначение: — число всех делителей а.

— сумма всех делителей числа а.

В дальнейшем будем использовать обозначение означающее, что суммирование идет по всем делителям а. Например, .

Пример 1: Делители числа 18 это 1,2,3,6,9,18. Поэтому

Пример 2: Пусть р — простое число. Тогда

.

Теорема 1: Пусть

Тогда

Доказательство: По следствию 1 п.4 любой делитель а имеет вид , где .

Показатель можно выбирать способом, а именно, 0,1,2,…. Показатель можно выбирать способом и т.д. Значит, общее число способом составить комбинацию равно произведению ,

а так как различным комбинациям соответствуют различные делители а, то .

■

Пример: Найти количество делителей числа а = 360.

Имеем .

Замечание: С геометрической точки зрения величина есть число точек с целыми координатами, лежащих на графике гиперболы координатной четверти.

Теорема 2: Пусть .

Тогда

Доказательство: Рассмотрим выражение Чтобы вычислить S раскроем скобки, перемножая по одному слагаемому из каждой скобки. Каждое такое произведение есть делитель а, поэтому S есть сумма всех делителей а, т.е.

С другой стороны, каждая из k скобок содержит геометрическую прогрессию со знаменателем . Применяя формулу суммы первых членов прогрессии, получим требуемое.

■

Пример: Найти сумму делителей числа а =360.

Имеем

В древнегреческой математике большой интерес вызывали числа, равные сумме своих собственных делителей (т.е. всех делителей числа а, кроме самого а). Пифагорейцы называли такие числа совершенными, приписывая им мистические свойства.

Определение: Число а называется совершенным, если т.е. если

Первые два совершенных числа это

6 = 1+2+3 и 28 = 1+2+4+7+14.

В древней Греции были еще известны совершенные числа 496 и 8128.

Евклид вывел формулу, позволяющую находить совершеннее числа, заметив закономерность:

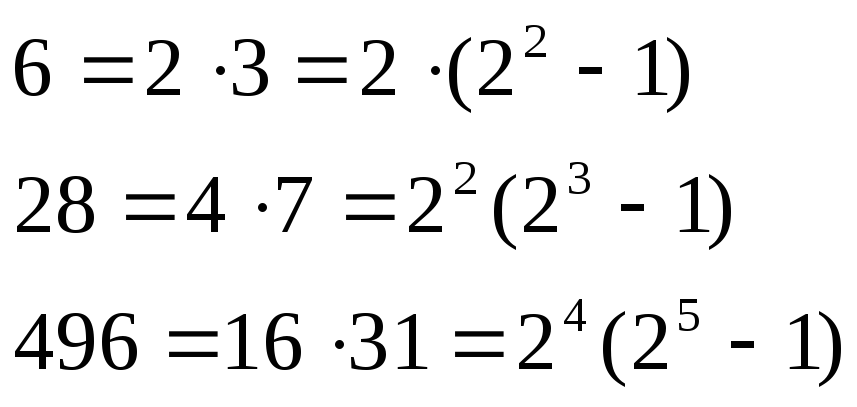
Теорема: (Евклид)

Пусть , причем — простое число.

Тогда а — совершенное число.

Доказательство:

Обозначим , тогда и по теореме 2

■

Замечание: Доказанная формула означает, что каждое простое число Мерсенна порождает совершенное число. Эйлер доказал, что этой формулой исчерпывается все множество четных чисел. Существуют ли нечетные совершенные числа, неизвестно.

Теорема: (Эйлер)

Пусть а — четное совершенное число. Тогда а можно представить в виде , где — простое число.

Доказательство: Число а — четное, значит его можно записать в виде , где b — нечетное, .

Из теоремы 2 следует, что .

С другой стороны, а — совершенное число, значит . Итак, .

Числа и взаимно просты b делится на , т.е.

, где с — собственный делитель b. Подставим это выражение в предыдущее равенство.

Получим .

Если , то число b имеет различные делители 1, с, b, значит, . Противоречие означает, что , а так как , то — простое число.

■

Помимо совершенных чисел, в древности выделяли так называемые дружественные числа.

Определение: Числа а и b называются дружественными, если

и ,

т.е сумма собственных делителей одного из чисел равна другому числу.

Из определения следует, что .

Совершенное число является дружественными самому себе.

Пара дружественных чисел а = 220, b = 284, была единственной, известной в Древней Греции.

Среди натуральных чисел < 1000000 найдено 42 пары дружественных чисел. Общий метод построения пар дружественных чисел неизвестен.