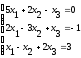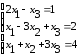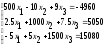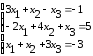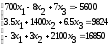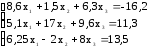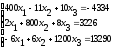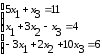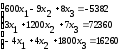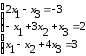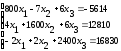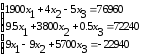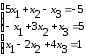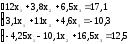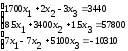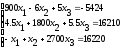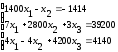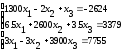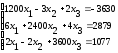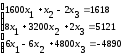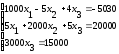7. Лабораторная работа №5

РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Целью работыисследовать методики решения систем линейных алгебраических уравнений (СЛАУ) в интегрированной среде MathCad

Содержание работы

1. Исследовать матричный метод (метод Крамера) решения СЛУ;

2. Исследоватьметод Гаусса;

3. Исследоватьметод простой итерации (метод Якоби);

Перечень необходимых материалов, реактивов, приборов, оборудования

Лабораторная работа проводится в компьютерном классе с сетевым оборудованием со следующим программным обеспечением: ОС MS Windows XP и выше, офисный пакет OpenOffice, система инженерных и математических расчетов MathCad.

Методические указания

1. Матричный метод (метод Крамера)

Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как

(7.1)

Эту систему уравнений можно записать также в матричном виде:

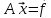(7.2)

где

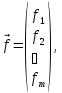
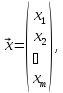
A– матрица системы,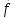– вектор правых частей,– вектор неизвестных.

При известных A и требуется найти такие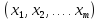, при подстановке которых в систему уравнений она превращается в тождество.

Необходимым и достаточным условием существования единственного решения СЛАУ является условие det A≠0, т.е. определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.

При небольшой размерности системы m (m = 2,…,5) на практике часто используют формулы Крамера для решения СЛАУ:

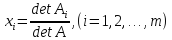
2. Метод Гаусса

Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений

(7.3)

первый элемент 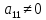. Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на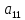и исключимиз всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при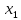в соответствующей строке. Получим

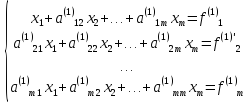(7.4)

Если , то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей

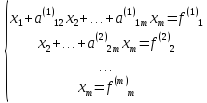(7.5)

Из нее в обратном порядке находим все значения

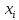
(7.6)

Процесс приведения к системе с треугольной матрицей называется прямымходом, а нахождения неизвестных –обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому предварительно необходимо выбирать главный элемент путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных так, чтобы выполнялось условие:

т.е. осуществляется выбор первого главного элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a₁₁был максимальным по модулю. Разделив первую строку на главный элемент, как и прежде, исключают x₁из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.

3. Метод простой итерации (метод Якоби)

Пусть требуется решить систему линейных уравнений, которая в матричном виде записывается как:

,

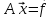где

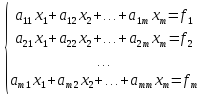(7.7)

Предположим, что диагональные элементы матриц A исходной системы не равны0(a_ii≠ 0,i= 1, 2, …, n).Разрешим первое уравнение системы относительно x₁, второе относительно x₂ и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:

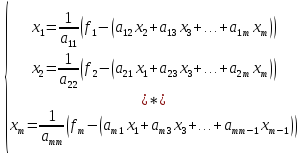(7.8)

Теперь, задав нулевое приближение , по рекуррентным соотношениям (5.8) можем выполнять итерационный процесс, а именно:

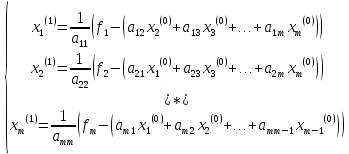(7.9)

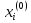Аналогично находятся следующие приближения , где в (5.9) вместонеобходимо подставить.

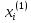Условие окончания итерационного процесса

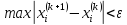(7.10)

Достаточное условие сходимости.

Если выполнено условие диагонального преобладания, т.е. ,

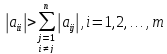
то итерационный процесс сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.

Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут

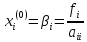(7.11)

или .

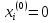Задание к лабораторной работе №5

Таблица 7.1 – Исходные данные для выполнения самостоятельного задания

№ В	Система линейных уравнений	№ В	Система линейных уравнений
1		13
2		14
3		15
4		16
5		17
6		18
7		19
8		20
9		21
10		22
11		23
12		24

Решить систему линейных уравнений:

1. Решить СЛАУ матричным методом и сравнить результаты с расчетом в среде Mathcad;

2. Решить СЛАУ методом Гаусса;

3. Решить СЛАУ методом простой итерации;

4. Решить СЛАУ методом Зейделя.

Содержание отчета

Отчет по лабораторной работе должен содержать:

1. Титульный лист, оформленный согласно приложению 1;

2. Условие задания и порядок выполнения расчетов.

3. Протокол работы в виде документа Mathcad с текстовыми блоками заголовков заданий и формульных блоков их выполнения по каждому пункту заданию согласно своему варианту;

4. Выводы о проделанной работе.

Контрольные вопросы

1. Объяснить суть метода решения СЛАУ метод Крамера;

2. Объяснить суть метода решения СЛАУ методом Гаусса;

3. Объяснить суть метода простой итерации. Условия сходимости метода;

4. Объяснить суть метода Зейделя. Условия сходимости метода.