Задание к лабораторной работе №3

Найти коэффициенты статической характеристики нагрузки по опытным данным для активной и реактивной мощности и определить их регулирующие эффекты. Данные приведены в относительных единицах в табл. 5.4.

Таблица 5.4

	0.82	0.86	0.91	0.95	1	1.05	1.09	1.15
	0.82	0.86	0.93	0.96	1	1.04	1.09	1.13
	0.61	0.69	0.79	0.90	1	1.13	1.27	1.41

Содержание отчета

Отчет по лабораторной работе должен содержать:

1. Титульный лист, оформленный согласно приложению 1;

2. Условие задания и порядок выполнения расчетов.

3. Протокол работы в виде документа Mathcad с текстовыми блоками заголовков заданий и формульных блоков их выполнения по каждому пункту заданию согласно своему варианту;

4. Выводы о проделанной работе.

Контрольные вопросы

1.Что такое статические характеристики нагрузки?

2.Что такое регулирующий эффект нагрузки?

3.Какие существуют основные виды электрических нагрузок?

4.Какие нагрузки не потребляют реактивной мощности?

5.Какой регулирующий эффект имеют печи сопротивления и лампы накаливания?

6.Как изменяется регулирующий эффект по реактивной мощности асинхронного двигателя при снижении напряжения?

7.Какие математические модели используются для моделирования электрической нагрузки в установившихся режимах?

8.Что такое типовые статические характеристики?

9.Какие схемы замещения используются для моделирования нагрузки?

6. Лабораторная работа №4 методы дифференцирование в задачах электротехники

Целью работы является исследование основных численных алгоритмов для решения обыкновенных дифференциальных уравнений.

Содержание работы

1. Численное решение обыкновенных дифференциальных уравнений методом Эйлера;

2. Численное решение обыкновенных дифференциальных уравнений усовершенствованным методом Эйлера.

3. Численное решение обыкновенных дифференциальных уравнений модифицированным методом (Эйлера-Коши).

4. Численное решение обыкновенных дифференциальных уравнений модифицированным методом Рунге-Кутты.

Перечень необходимых материалов, реактивов, приборов, оборудования

Лабораторная работа проводится в компьютерном классе с сетевым оборудованием со следующим программным обеспечением: ОС MS Windows XP и выше, офисный пакет OpenOffice, система инженерных и математических расчетов MathCad.

Методические указания

1. Метод Эйлера

Дифференциальным называется уравнение, содержащее один или несколько производных. В зависимости от количества не зависимых переменных, дифференциальные уравнения делятся на две категории.

1. Обыкновенные дифференциальные уравнения (ОДУ)

2. Дифференциальные уравнения в частных производных.

Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции 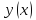. Их можно записать виде

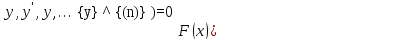(6.1)

независимая переменная

Наивысший порядок 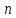, входящий в уравнение (6.1) называется порядком дифференциального уравнения.

Простейшим (линейным) ОДУ является уравнение (1) разрешенное относительно производной

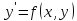(6.2)

Решением дифференциального уравнения (1) называется всякая функция, 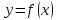которая после ее подстановки в уравнение обращает его в тождество.

Основная задача, связанная с линейной ОДУ известно как задача Каши: найти решение уравнения (2) в виде функции 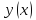удовлетворяющий начальному условию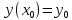(6.3)

Геометрически это означает, что требуется найти интегральную кривую, 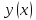проходящую через точку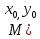) при выполнение равенства (2).

Численный с точки зрения задачи Каши означает: требуется построить таблицу значений функции 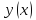удовлетворяющий уравнение (6.2) и начальное условие (6.3) на отрезке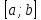с некоторым шагом. Обычно считается, чтото есть начальное условие задано в левом конце отрезка.

Простейшим из численных методов решения дифференциального уравнения является метод Эйлера. В его основе лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной форме или таблицы.

Пусть дано уравнение с начальным условием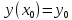то есть поставлена задача Каши. Решим вначале следующую задачу. Найти простейшим способом приближенное значение решения в некоторой точкегде-достаточно малый шаг. Уравнение (6.2) совместно с начальным условием (6.3) задают направление касательной искомой интегральной кривой в точке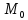с координатами

Уравнение касательной имеет вид

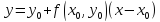
Двигаясь вдоль этой касательной, получим приближенное значение решения в точке :

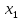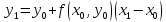
или

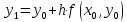(6.4)

Располагая приближенным решением в точке 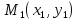можно повторить описанную ранее процедуру: построить прямую проходящую через эту точку с угловым коэффициентом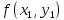, и по ней найти приближенное значение решения в точке.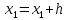

Заметим, что эта прямая не является касательной к реальной интегральной кривой, поскольку точка 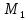нам не доступна, однако еслидостаточно мало то получаемые приближенные будут близки к точным значениям решения.

Продолжая эту идею, построим систему равно отстоящих точек

.

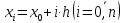Получение таблицы значений искомой функции 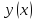по методу Эйлера заключается в циклическом применение формулы

(6.5)

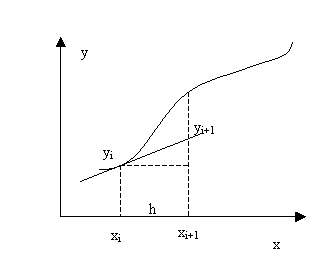
Рисунок. 6.1. Геометрическая иллюстрация метода Эйлера

Решение ОДУ в некоторой точке x_iназывается устойчивым, если найденное в этой точке значение функции y_iмало изменяется при уменьшении шага интегрирования. Для проверки устойчивости, таким образом, надо провести два расчета значения (y_i) – с шагом интегрирования 2h и при уменьшенной (например, двое) величине шага. В качестве критерия устойчивости можно использовать малость относительного изменения полученного решения при уменьшении шага интегрирования

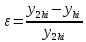
где 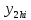- решение, рассчитанное с шагом 2h,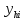– решение, рассчитанное с

шагом h.