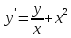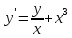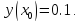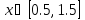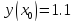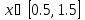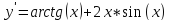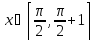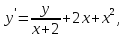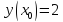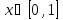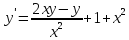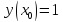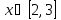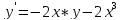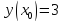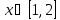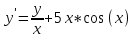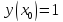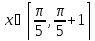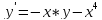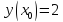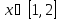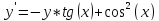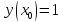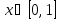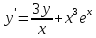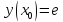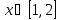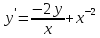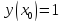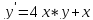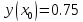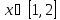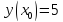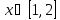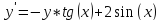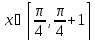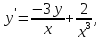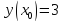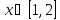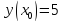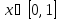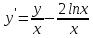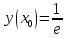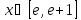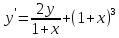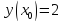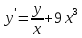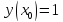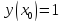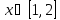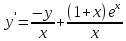2. Модифицированный метод (Эйлера-Коши)
Повысить точность и устойчивость вычисления решения можно с помощью неявного метода Эйлера следующего вида.
Прогноз:
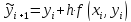(6.10)
Коррекция:
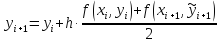(6.11)
Геометрически это означает, что с начало
определяется направление интегральной
кривой в исходной точке
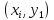и во вспомогательной точке
,
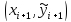а в качестве окончательного направления
берется среднее значение этих направлений.
Благодаря более точной формуле интегрирования, погрешность метода пропорциональна уже квадрату шага интегрирования.
Задание к лабораторной работе №4
Таблица 6.1 – Исходные данные для выполнения самостоятельного задания
|
№ варианта |
Функции |
Начальные условия |
Интервал |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
14 |
|
|
|
|
15 |
|
|
|
|
16 |
|
|
|
|
17 |
|
|
|
|
18 |
|
|
|
|
19 |
|
|
|
|
20 |
|
|
|
|
21 |
|
|
|
|
22 |
|
|
|
Вариант выполнения работы соответствует порядковому номеру в журнале проведения занятий преподавателя. Данные выбираются из табл.6.1.
Для заданной функции y = f(x) выполнить следующее:
1. Подобрать оптимальный шаг интегрирования дифференциального уравнение методом Эйлера при котором относительное изменение решения составит 5%. Первоначальный шаг hвыбрать равным 1/10 интервала интегрирования. Последующие шаги уменьшать в 2 раза. Используя программу расчета в средеMathcadпроверить результаты.
2. Решить дифференциальное уравнение усовершенствованный методом Эйлера взяв шаг интегрирования из пункта 1. Проверить результаты используя Mathcad.
3. Решить дифференциальное уравнение модифицированным методом Эйлера-Коши взяв шаг интегрирования из пункта 1. Проверить результаты используя Mathcad.
4. Решить дифференциальное уравнение методом Рунге-Кутты взяв шаг интегрирования из пункта 1. Проверить результаты используя Mathcad.
5. Сравнить точность расчетов приведенных методом.
Содержание отчета
Отчет по лабораторной работе должен содержать:
1. Титульный лист, оформленный согласно приложению 1;
2. Условие задания и порядок выполнения расчетов.
3. Протокол работы в виде документа Mathcad с текстовыми блоками заголовков заданий и формульных блоков их выполнения по каждому пункту заданию согласно своему варианту;
4. Выводы о проделанной работе.
Контрольные вопросы
1. Объяснить суть решения дифференциального уравнения методом Эйлера.
2. Объяснить суть решения дифференциального уравнения усовершенствованный методом Эйлера .
3. Объяснить суть решения дифференциального уравнения модифицированным методом Эйлера-Коши.
4. Объяснить суть решения дифференциального уравнения методом Рунге-Кутты .