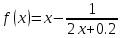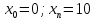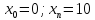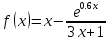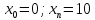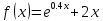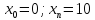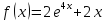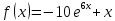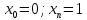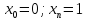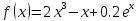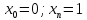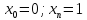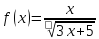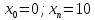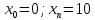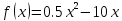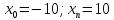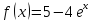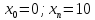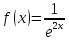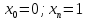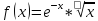4. Лабораторная работа №2

ИНТЕРПОЛИРОВАНИЕ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТОВ

Целью работы является изучение методов и алгоритмов интерполирования и аппроксимации функций и реализации их в MathCad.

Содержание работы

1. Исследование локальных методов интерполирования результатов эксперимента;

2. Исследование глобальные методов интерполирования результатов эксперимента.

Перечень необходимых материалов, реактивов, приборов, оборудования

Лабораторная работа проводится в компьютерном классе с сетевым оборудованием со следующим программным обеспечением: ОСMSWindowsXPи выше, офисный пакет OpenOffice, система инженерных и математических расчетовMathCad.

Методические указания

Аппроксимация - приближенное выражение сложной функции с помощью более простых.

Интерполя́ция - способ нахождения промежуточных значенийвеличины по имеющемусядискретномунабору известных значений.

К интерполяционным методам можно отнести: кусочно-постоянную, кусочно-линейную интерполяцию, кубический интерполяционный сплайн, интерполяционный многочлен Лагранжа.

1. Кусочно-постоянная интерполяция

На каждом отрезке 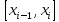  интерполяционный многочлен равен константе, а именно левому или правому значению функции.

Для левой кусочно-линейной интерполяции , т.е.

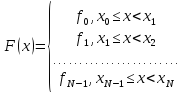
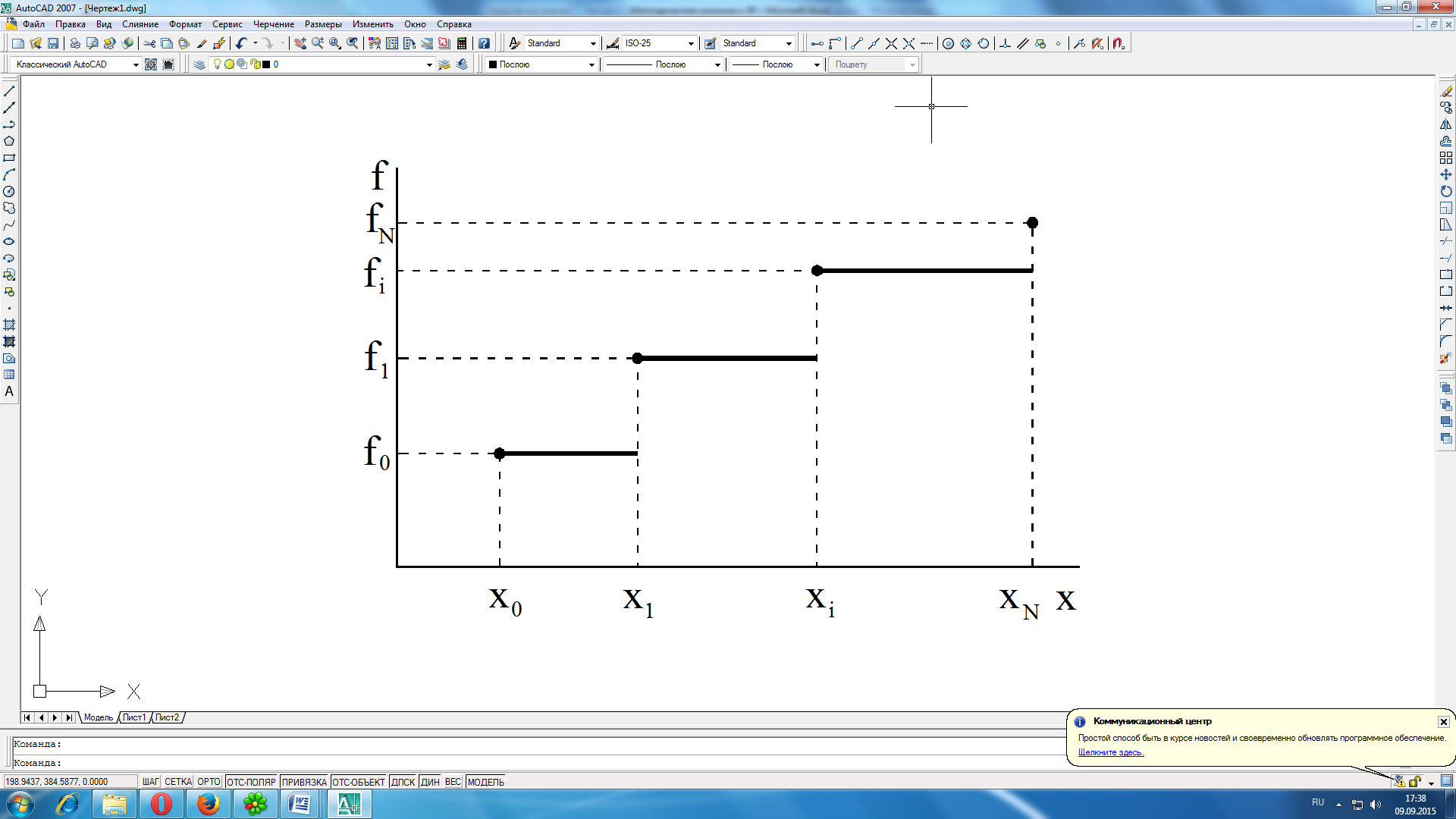
Рисунок 2.1 Левая кусочно-постоянная интерполяция

Для правой кусочно-линейной интерполяции , т.е.

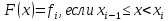
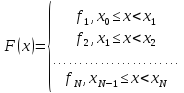
Рисунок 2.2 Правая кусочно-постоянная интерполяция

2. Кусочно-линейная интерполяция

На каждом интервале 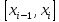 функция является линейной .

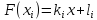Значения коэффициентов находятся из уравнений:

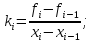
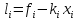
Функцию 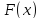на каждом интервале можно записать в виде:

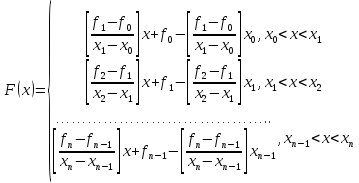
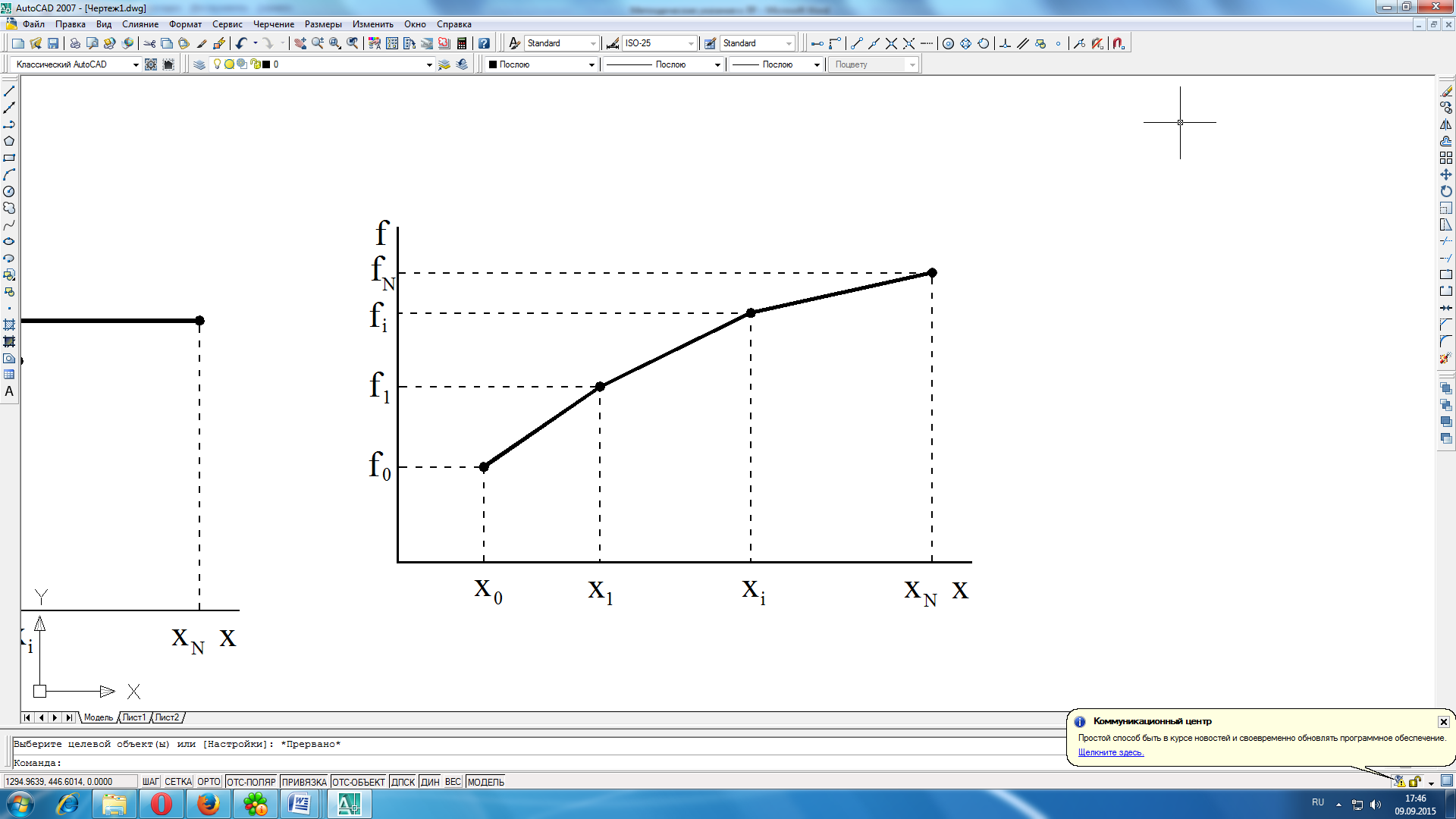
Рисунок 2.3 кусочно-линейной интерполяция

3. Интерполяционный многочлен Лагранжа

Интерполяционный многочлен Лагранжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек.

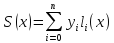
где базисные полиномы определяются по формуле:

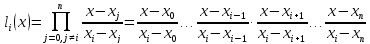
Для трех узлов интерполяции N=2

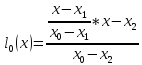
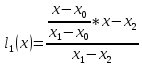
- уравнение, проходящей через точки (x0, y0), (x1, y1), (x2, y2)

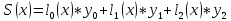
Задание к лабораторной работе №2

Таблица 2.1 – Исходные данные для выполнения самостоятельного задания

№	Функции	Интервал
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Вариант выполнения работы соответствует порядковому номеру в журнале проведения занятий преподавателя. Данные выбираются из табл.2.1.

Для заданной функции f(x) выполнить следующее:

1. Разбить исходный интервал [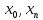] на 10 равных интервалов.

2. Записать уравнения для кусочно-постоянной интерполяции (левой и правой). Изобразить графически интерполирующие и заданную функцию. Используя Mathcad, определить интегральную ошибку интерполирования.

3. Повторить пункты 2-4 для кусочно-линейной интерполяции.

4. Записать уравнения многочлена Лагранжа для степеней от 2 до 5. Применив MatCad изобразить графически интерполирующие функции. Определить интегральные ошибки.

Содержание отчета

Отчет по лабораторной работе должен содержать:

1. Титульный лист, оформленный согласно приложению 1;

2. Условие задания и порядок выполнения расчетов.

3. Протокол работы в виде документа Mathcad с текстовыми блоками заголовков заданий и формульных блоков их выполнения по каждому пункту заданию согласно своему варианту;

4. Выводы о проделанной работе.

Контрольные вопросы

1. Что называется интерполяцией и аппроксимацией функции? Чем отличается локальная интерполяция от глобальной?

2. Объяснить суть метода кусточно-постоянной и кусочно -линейной интерполяций.

3. Объяснить методику определения коэффициентов уравнений кусочно -линейной интерполяций. От чего зависит точность интерполирования?

4. Какие условия накладываются на сплайн-функцию?

5. Из каких уравнений определяются коэффициенты сплайн-функции?

6. Объяснить методику получения многочлена Лагранжа. Как зависит точность интерполяции от количества узлов?