
РДЗ 20 Вариант / Методички / 1
.pdfМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Запорізький національний технічний університет
МЕТОДИЧНІ ВКАЗІВКИ ТА РОЗРАХУНКОВО-ГРАФІЧНІ ЗАВДАННЯ
до контрольних робіт з вищої математики (розділи: кратні інтеграли, елементи теорії поля, теорія функції комплексної змінної, операційне числення)
для студентів ФРЕТ та ФКНТ заочної форми навчання
2015
PDF created with pdfFactory Pro trial version www.pdffactory.com
Методичні вказівки та розрахунково-графічні завдання до контрольних робіт з вищої математики (розділи: кратні інтеграли, елементи теорії поля, теорія функції комплексної змінної, операційне числення) для студентів ФРЕТ та ФКНТ заочної форми навчання./ Укл.: Т.І.Левицька, Г.А.Шишканова, І.А.Пожуєва. – Запоріжжя:
ЗНТУ, 2015. – 86 с.
Містить розрахунково-графічні завдання, теоретичні відомості та приклади виконання завдань з курсу “Вища математика” за темами: кратні інтеграли, елементи теорії поля, теорія функції комплексної змінної, операційне числення для студентів ФКНТ та ФРЕТ заочної форми навчання.
Укладачі: Т.І. Левицька, доцент, к.т.н.
Г.А. Шишканова, доцент, к.ф.-м.н. І.С. Пожуєва, доцент, к.т.н.
Експерт: Кабак В.С., Касьян М.М.
Рецензент: Мастиновський Ю.В., доцент,к.т.н.
Відповідальний за випуск: Т.І. Левицька, доцент, к.т.н.
Затверджено на засіданні кафедри
прикладної математики Протокол № 6 від 28.01.15
PDF created with pdfFactory Pro trial version www.pdffactory.com
|
3 |
|
|
ЗМІСТ |
|
1 |
КРАТНІ ІНТЕГРАЛИ ТА ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ....…4 |
|
1 |
.1 Подвійний інтеграл……….......………….…………..........4 |
|
1 |
.2 Криволінійний інтеграл. ….......…………….…………....8 |
|
1 |
.3 Теорія поля. ………………………......……....................11 |
|
2 |
ТЕОРІЯ ФУНКЦІЙ КОМПЛЕКСНОЇ ЗМІННОЇ............... |
18 |
2 |
.1 Комплексні числа та дії над ними............................... |
18 |
2 |
.2 Основні елементарні функції комплексної змінної...... |
23 |
2 |
.3 Аналітичні функції.................................................... |
26 |
2 |
.4 Інтегрування функції комплексної змінної................. |
27 |
2 |
.5 Інтегральна формула Коші......................................... |
31 |
2 |
.6 Ряди Тейлора та Лорана............................................. |
33 |
2 |
.7 Нулі аналітичної функції.......................................... |
40 |
2 |
.8 Ізольовані особливі точки......................................... |
41 |
2 |
.9 Лишки...................................................................... |
42 |
3 |
ОПЕРАЦІЙНЕ ЧИСЛЕННЯ.......................................... |
45 |
3 |
.1 Визначення перетворення Лапласа. Оригінал та |
|
зображення функції........................................................ |
45 |
|
3 |
.2 Властивості перетворення Лапласа............................ |
47 |
3 |
.3 Знаходження оригінала по зображенню..................... |
52 |
3 |
.4 Розв’язання задачі Коші для звичайних лінійних |
|
диференціальних рівнянь з постійними коефіцієнтами.... |
55 |
|
4 |
РОЗРАХУНКОВО-ГРАФІЧНІ ЗАВДАННЯ.……..……….57 |
|
4 |
.1 Завдання 1…………………………….............................57 |
|
4 |
.2 Завдання 2…………………………….............................61 |
|
4 |
.3 Завдання 3…………………………….............................63 |
|
4 |
.4 Завдання 4…………………………….............................64 |
|
4 |
.5 Завдання 5…………………………….............................67 |
|
4 |
.6 Завдання 6…………………………….............................68 |
|
4 |
.7 Завдання 7…………………………….............................70 |
|
4 |
.8 Завдання 8…………………………….............................71 |
|
4 |
.9 Завдання 9…………………………….............................73 |
|
4 |
.10 Завдання 10……………………………..........................73 |
|
4 |
.11 Завдання 11……………………………..........................74 |
|
4 |
.12 Завдання 12……………………………..........................75 |
|
4 |
.13 Завдання 13……………………………..........................78 |
|
4 |
.14 Завдання 14……………………………..........................81 |
|
Контрольні питання..................................................................................... |
83 |
|
Література………………..……………...................….………...86
PDF created with pdfFactory Pro trial version www.pdffactory.com
4
1 КРАТНІ ІНТЕГРАЛИ ТА ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ
1.1 Подвійний інтеграл
Приклад 1.1
Змінити порядок інтегрування в інтегралі:
1 |
|
1− x2 |
|
|
|
òdx |
|
|
ò f (x; y)dy |
||
−1 |
− |
|
1− x |
2 |
|
|
|
|
|
||
Розв’язок:
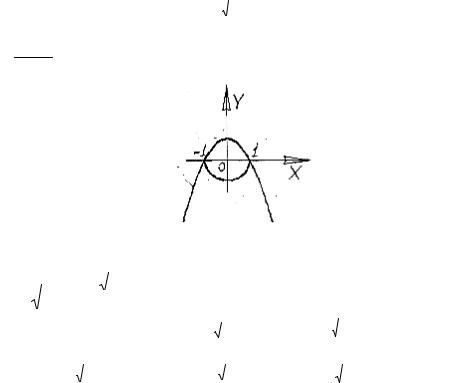
. Область інтегрування D обмежена лініями х = -1; х = 1 , у = -

 1− x2 ;у = 1 - х 2
1− x2 ;у = 1 - х 2
Рисунок 1.1 Змінимо порядок інтегрування, для чого задану область
уявимо у вигляді двох областей: Dl-обмежену зліва i справа вітками |
||||||||||||||
параболи x = ± 1− y |
(0 ≤ у ≤ l), i D2 |
обмежену дугами кола |
||||||||||||
x= ± 1− y2 |
(-1 ≤ у ≤ 0). |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
|
1− x2 |
|
|
|
|
|
|
1− y2 |
|
|||||
1 |
1 |
1− y |
0 |
|||||||||||
Тоді òdx |
|
|
ò f (x, y)dy = òdy |
|
ò f (x, y) + òdy |
|
|
ò f (x, y)dx |
||||||
−1 |
− |
1− x2 |
|
0 |
− 1− y |
−1 |
− |
1− y2 |
|
|||||
Приклад 1.2 |
|
|
|
|
|
|
лініями x − 4y + 7 = 0 , |
|||||||
Обчислити |
площу |
фігури, |
обмеженої |
|||||||||||
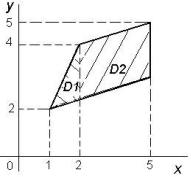
x − 4y +14 = 0, 2x − y = 0 , x = 5 . Зобразити фігуру.
PDF created with pdfFactory Pro trial version www.pdffactory.com
5
Розв’язок:
Зобразимо фігуру (рис. 1.2). Площа фігури: S = òòdxdy . Область
D
інтегрування розіб’ємо на дві частини D1 та D2 . Площу шуканої фігури обчислимо, як суму площ цих областей:
S = S1 + S2 = òòdxdy + òòdxdy . Знайдемо кожен з цих інтегралів:
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
D2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2x |
|
2 |
æ |
|
|
|
x + 7 |
ö |
|
7 (x -1)2 |
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
S1 = òòdxdy = òdx |
|
òdy = òç |
2x - |
|
|
|
÷dx = |
|
|
|
|
= |
|||||||||||||||||||||
4 |
|
4 2 |
|||||||||||||||||||||||||||||||
|
D |
|
|
|
|
|
|
|
|
0 |
|
(x+7)/ 4 |
0 |
è |
|
|
|
|
ø |
|
|
|
1 |
||||||||||
|
1 |
|
7 |
|
|
1 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
× |
= |
|
(кв. одиниць). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
4 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
2 |
|
|
|
|
(x+14) / 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
òò |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
æ x +14 |
|
|
x + 7 ö |
|
21 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
ò |
|
|
ò |
|
|
|
ò |
è |
|
4 |
|
|
|
4 ø |
|
4 |
|
|
|
|||||
S2 = |
|
dxdy |
= |
|
|
dx |
|
|
|
dy |
= |
|
ç |
|
|
|
- |
|
|
÷dx = |
|
(кв.одиниць). |
|||||||||||
|
D2 |
|
|
|
|
|
|
|
|
2 |
|
|
(x+7) / 4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Тоді, площа даної фігури: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
S = |
|
7 |
+ |
21 |
|
= |
|
49 |
= 6 |
1 |
(кв. одиниць). |
|
|
|
|
|
||||||||||||||||
|
8 |
|
8 |
8 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Рисунок 1.2
PDF created with pdfFactory Pro trial version www.pdffactory.com
|
|
6 |
|
Приклад 1.3 |
|
|
|
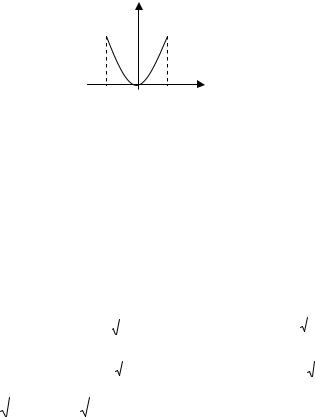
Обчислити òò(x + 2y)dxdy |
D : y = x2; y = 4 |
||
D |
|
|
|
|
|
y |
|
|
|
4 |
|
-2 |
o 2 x |
||
Розв’язок: |
Рисунок 1.3 |
||
|
|
||
1-й спосіб. |
|
|
|
|
2 |
4 |
2 |
|
|
|
|
|
|
4 |
òò(x + 2y)dxdy = ò dx ò |
(x + 2y)dy = ò (xy + y2) |
|
||||||||
|
x2 |
|||||||||
D |
−2 |
x2 |
−2 |
|
|
|
|
|
|
|
|
2 |
|
|
x4 |
|
|
2 |
|||
|
|
|
|
|||||||
= ò (4x +16 - x3 - x4)dx = (2x2 +16x - |
- |
x5 |
) |
|
|
|||||
|
|
|||||||||
|
−2 |
|
4 |
|
5 |
|
−2 |
|||
|
|
|
|
|
|
|||||
dx =
= 2565
2-й спосіб ( зміна порядку інтегрування ).
|
|
|
|
|
|
|
4 |
|
|
|
y |
|
|
4 |
x2 |
|
|
|
|
y |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
òò(x + 2y)dxdy = òdy |
ò |
|
|
(x + 2y)dx = ò( |
+ 2yx) |
|
|
|
|
dy = |
|||||||||||||||||
|
|
2 |
|||||||||||||||||||||||||||
|
|
D |
|
|
|
|
0 |
|
|
− |
|
y |
|
|
0 |
|
|
|
− |
|
|
y |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
5 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= ò( |
y |
+ 2y |
y |
- |
y |
+ 2y |
|
y |
)dy = 4òy2 dy = |
8 |
y2 |
|
|
= |
256 |
|
|
|
|
|
|
||||||||
2 |
|
5 |
|
|
|
|
|
|
|||||||||||||||||||||
0 |
|
2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
5 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Приклад 1.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Обчислити |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
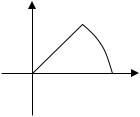
òòln(4 + x2 + y2 )dxdy |
D : x2 + y2 = 4; y = x; y = 0; (x ³ 0) |
|
|
|
|
||||||||||||||||||||||||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PDF created with pdfFactory Pro trial version www.pdffactory.com
7
y
x
о2x
Рисунок 1.4
Розв’язок:
Обчислення подвійного інтеграла краще провести у полярній системі координат. Перехід від декартових до полярних координат
здійснюється за формулами x = ρcosϕ; y = ρsin ϕ. |
Рівняння кола |
|||||||||||||
x2 + y2 = 4 у полярній |
системі координат буде |
мати вигляд |
||||||||||||
ρ2 cos2 ϕ + ρ2 sin 2 ϕ = 4 |
|
|
|
|
або |
ρ = 2 . |
|
|||||||
|
|
|
Тоді òòln(4 + x2 + y2 )dxdy = |
|
||||||||||
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
= òòln(4 + ρ2 cos2 ϕ + ρ2 sin 2 ϕ)ρdϕdρ = |
|
|||||||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
2 |
|
|
π |
2 |
|
|
|
|
||||
|
4 |
|
1 |
|
4 |
|
|
|
|
|
||||
= òdϕòln(4 + ρ2)ρdρ = |
|
òdϕòln(4 + ρ2 )d(4 + ρ2) = |
|
|||||||||||
2 |
|
|||||||||||||
0 |
|
0 |
0 |
|
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
= π |
(4 + ρ2 )(ln(4 + ρ2 ) −1) |
|
2 = π(2ln 2 − |
1 |
) . |
|
||||||||
|
|
|||||||||||||
|
|
|
||||||||||||
8 |
|
|
|
|
0 |
|
2 |
|
|
|||||
|
|
|
|
|
||||||||||
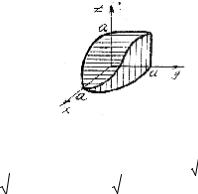
Приклад 1.5.
ìïx2 + y2 = a2
Обчислити об'єм тіла, обмеженого поверхнями íïx2 + z2 = a2
î
Розв’язок:
Розглянемо восьму частину заданого тіла:
V= òò f (x, y)dxdy
D
PDF created with pdfFactory Pro trial version www.pdffactory.com
8
Рисунок 1.5
1 |
|
|
a |
|
|
a2 −x2 |
|
|
V= òò |
a2 - x2 dxdy = ò a2 - x2 dx |
òdy = |
||||||
8 |
||||||||
D |
0 |
|
|
0 |
|
|||
|
|
|
|
|||||
a
ò
0
|
æ |
x3 ö |
|
a |
|
2 |
|
16 |
|
||
|
|
|
|
|
|||||||
(a2 |
- x2 )dx =ç a2x - |
|
÷ |
|
|
= |
|
a3 . V= |
|
|
a3 (куб.од.) |
|
|
|
|
|
|
||||||
|
ç |
3 |
÷ |
|
0 |
|
3 |
|
3 |
|
|
|
è |
ø |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
1.2 Криволінійний інтеграл
Приклад 1.6
Обчислити криволінійний інтеграл.
(B)
I = ò xydx + ( y - x)dy - вздовж ліній y = x2 та x = y2 між
( A)
точками А(0,0) та В(1,1)
Розв’язок:
|
b |
|
¢ |
òP(x, y)dx + Q(x, y)dy = ò(P(x, y(x)) + Q(x, y(x))y (x))dx |
|
L |
a |
Нижня та верхня межа інтеграла подані початковою та кінцевою точками. У першому випадку за параметр беремо х.dy=2xdx
I= ò1 [x × x2 + (x2 - x) *2x]dx = ò1 (3x2 - 2x2)dx = 3 |
x4 |
|
1 - 2 |
x3 |
|
1 = |
|
1 |
|
|
|
||||||||
4 |
|
3 |
|
12 |
|||||
0 |
0 |
|
0 |
|
0 |
||||
|
|
|
|
|
|||||
У другому випадку за параметр беремо y. Тоді dx= 2ydy
PDF created with pdfFactory Pro trial version www.pdffactory.com

9
I = ò1 [(y2 * y)2y + (y − y2)]dy = ò1 (2y4 + y − y2 )dy = 2 |
y5 |
|
|
1 + |
y2 |
|
|
1 - |
||||||||||||||
|
|
|
||||||||||||||||||||
5 |
2 |
|||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
- |
y3 |
|
1 |
= |
2 |
+ |
1 |
− |
1 |
= |
17 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
|
|
0 |
5 |
2 |
3 |
30 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Маємо різні результати, тому що інтегрування проводилося за різними кривими.
Приклад 1.7.
Обчислити ò(7x − 2y)dl де l: відрізок прямої від точки A(1,2) до
l
точки B(3,5) .
y
B
 A
A
o 



 x
x
Рисунок 1.6
Розв’язок:
Знайдемо рівняння прямої, яка проходить через дві задані точки.
y − yA |
|
= |
x − xA |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
yB − yA |
|
xB − xA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y − 2 |
x −1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
y′ = |
3 |
|
|||||||
|
= |
|
|
|
|
. Звідкіля маємо y = |
|
|
x |
+ |
|
; |
|
; |
|||||||||||
5−2 |
|
|
3−1 |
2 |
2 |
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
9 |
|
13 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
′2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
dl = 1+ y |
dx = |
1+ |
4dx = |
|
dx . |
|
|
|
|
|
|
||||||||||||||
2 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|||
|
ò(7x − 2y)dl = ò(7x − 3x −1) |
|
dx = |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
l |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
PDF created with pdfFactory Pro trial version www.pdffactory.com
|
|
|
|
|
|
|
|
10 |
|
|
||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
13 |
13 |
(2x2 |
|
|
3 = 7 |
|
|
||||
= |
|
ò(4x −1)dx = |
− x) |
|
13 |
. |
||||||
2 |
|
2 |
||||||||||
|
1 |
|
|
|
1 |
|
|
|||||
|
|
|
||||||||||
Приклад 1.8
Обчислити ò(3x + 2y)dx + xydy ;l : y = x2 +1 ;від x1 = 0 до x2 = −2
l
|
|
|
|
|
y |
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x |
-2 |
|
|
|
|
o |
|
||
|
|
|
|
|
||||
|
|
|
||||||
Рисунок 1.7
Розв’язок:
З рівняння лінії l знаходимо dy = d(x2 +1) = 2xdx .
Таким чином
−2
ò(3x + 2y)dx + xydy = ò(3x + 2(x2 +1) + x(x2 +1)2x)dx =
l |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
−2 |
−2 |
|
|
|
|
|
|
|
|
x |
2 |
|
x |
3 |
|
x |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= ò (3x + 4x2 |
+ 2x4 |
+ 2)dx = (3 |
|
+ 4 |
|
+ 2 |
|
+ 2x) |
= |
|||||||||
|
|
|
|
|
|
|||||||||||||
0 |
|
|
|
|
|
|
2 |
3 |
5 |
|
0 |
|||||||
32 |
|
64 |
|
|
|
322 |
|
|
|
|
|
|
|
|
|
|
||
= 6 − |
− |
|
− 4 = − |
. |
|
|
|
|
|
|
|
|
|
|
||||
3 |
5 |
|
15 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Приклад 1.9
Відновити функцію u = u(x, y) по ії повному диференціалу du = (2xy3 + 4)dx + (3x2 y2 + 3)dy .
Розв’язок:
Перевіримо, що це повний диференціал. Для цього повинна
виконуватись умова |
∂P |
= |
∂Q |
, P та Q вирази при dx та dy в |
|
∂y |
|
∂x |
|
диференціалі du = Pdx + Qdy .
PDF created with pdfFactory Pro trial version www.pdffactory.com
