
РДЗ 20 Вариант / Методички / 1
.pdf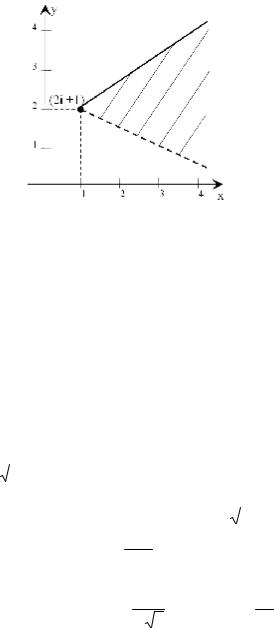
21
Рисунок 2.3
Приклад 2.2
Зобразити лінію, для якої Re z2 = a2
Розв’язок
а) Знайдемо z2 : z2 = (x + iy)2 = x2 − y2 + i2xy , тоді Re z2 = x2 − y2 ,
тобто рівняння Re z2 = a2 можна записати так: x2 − y2 = a2
Це, як відомо, рівнобічна гіпербола.
Для піднесення в степінь використовують формулу Муавра:
|
|
|
zn = ρ n (cos nϕ + i sin nϕ) |
(2.10) |
|
Приклад 2.3 |
|
|
|
|
|
Обчислити (− |
|
|
− i)5 |
|
|
|
3 |
|
|
||
Розв’язок |
тригонометричну форму числа (− |
|
− i). Для цього |
||
а) Знайдемо |
|
||||
3 |
|||||
знайдемо його модуль за формулою (2.1):
ρ = 
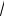 3 +1 = 2
3 +1 = 2
Та аргумент за формулою (2.2):
ϕ = arg z = −π + arctg −−13 = −π + π6 = − 56π
PDF created with pdfFactory Pro trial version www.pdffactory.com

|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тоді за формулою (2.4): |
|
|
|
|
|
|
5π ö |
|
|
|
|
|
|
5π öö |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
æ |
|
æ |
|
|
|
|
|
æ |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
- |
3 - i = 2çcosç |
- |
|
|
|
|
÷ |
+ i sinç |
- |
|
|
÷÷ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ç |
|
è |
|
|
|
6 ø |
|
|
|
|
è |
|
6 |
÷ |
||||||
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
øø |
||||||||||
Використовуючи формулу (2.10), одержуємо: |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
5 |
|
|
5æ |
æ |
25π ö |
|
|
æ |
|
|
25π öö |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
(- 3 |
- i) |
= 2 |
çcosç- |
|
|
|
÷ + i sinç |
- |
|
|
|
|
÷÷ = |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
ç |
è |
|
6 |
ø |
|
|
è |
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
||||
|
|
|
|
|
è |
|
|
|
|
|
|
|
6 øø |
|
|
|
|
|
|
|||||||||||
æ |
|
|
π |
|
|
|
|
π |
|
|
ö |
|
æ |
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
||
æ |
|
ö |
æ |
|
ö |
|
3 |
|
|
1 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
ç |
|
|
|
÷ |
|
|
|
|
|
|
|||||||||||||||||
= 32çcosç |
- |
|
÷ + i sinç |
- |
|
÷ |
÷ |
|
|
|
|
|
|
- i |
|
|
=16 |
3 -16i |
||||||||||||
|
|
= 32 |
|
|
|
|
|
|
|
|
÷ |
|||||||||||||||||||
ç |
è |
|
6 ø |
è |
|
6 |
ø |
÷ |
|
ç |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
||||||||
è |
|
|
ø |
|
è |
|
|
|
|
ø |
|
|
|
|
|
|
||||||||||||||
Корені степеня n визначаються за формулою:
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
ϕ + 2kπ |
|
|
|
|
|
ϕ + 2kπ ö |
|
|
|
|
||||||||
|
|
z = n |
|
|
|
|
|
|
|
|
|
|
+ isin |
|
|
|
k = 0,1,2....n -1 (2.11) |
|||||||||||||||||||||||
|
|
|
|
|
ρçcos |
|
|
n |
|
|
|
n |
÷, |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|||||||||
Приклад 2.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Знайти а) 3 |
|
|
|
|
; |
|
|
|
б) |
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1+ i |
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Розв’язок: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
а) Для числа 1+і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
π |
|||||||||||||||||||||||
| z |= |
|
|
|
|
= |
|
|
|
|
|
|
|
|
ϕ = arg z = arctg |
= |
|||||||||||||||||||||||||
1+1 |
|
|
2; |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
4 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|||||||
1+ i = |
|
|
|
|
æ |
|
|
|
|
|
|
|
+ i sin |
ö |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2çcos |
4 |
|
4 |
÷ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
||||||||
Використовуючи формулу (2.11): |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
π |
+ 2πk |
|
π |
+ 2πk |
ö |
|
|||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
ç |
|
|
|
|
|
|
4 |
|
4 |
÷ |
|
|||||||||||
3 |
1 |
+ i |
= |
2 |
2 |
|
ç |
cos |
|
|
|
|
|
+ i sin |
|
|
|
÷ |
k = 0,1, 2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
ç |
|
|
3 |
|
|
|
|
3 |
|
|
, |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
ми одержимо три різних значення кореня:
z = 6 |
|
æ |
|
π |
+ i sin |
|
π |
ö |
(k = 0) |
|
|||||||||
2çcos |
|
|
|
|
÷, |
||||
|
|
|
|
||||||
1 |
è |
12 |
|
12 |
ø |
|
|||
|
|
|
|||||||
PDF created with pdfFactory Pro trial version www.pdffactory.com
23
z2 |
= 6 |
|
|
æ |
9π |
+ isin |
9π |
ö |
|||
|
|
||||||||||
2çcos |
|
|
|
|
÷, |
||||||
12 |
|
12 |
|||||||||
|
|
è |
|
|
|
ø |
|||||
z |
= 6 |
|
æ |
17π |
|
+ isin |
17π |
||||
|
|
||||||||||
2çcos |
|
|
|
|
|
||||||
|
|
|
|
|
|||||||
3 |
|
è |
12 |
|
|
|
12 |
||||
|
|
|
|
|
|||||||
б) для числа z=1: ρ =1; ϕ =
3 |
|
= cos |
2πk |
+ i sin |
2πk |
, |
|
|
|
|||||||||
1 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
||||||
z1 = cos0 + i sin 0 =1, |
|
|
|
|
(k |
|||||||||||||
z2 |
= cos |
2π |
+ i sin |
2π |
|
|
= - |
|
1 |
|
||||||||
|
|
|
|
|
2 |
|
||||||||||||
|
|
3 |
|
3 |
|
|
|
|
|
|||||||||
z |
= cos |
4π |
|
+ i sin |
4π |
|
= - |
1 |
|
|||||||||
|
|
|
|
|||||||||||||||
3 |
3 |
|
3 |
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
(k =1) |
|
ö |
(k = |
2) |
÷, |
||
ø |
|
|
0 , за формулою (2.11):
k= 0,1, 2
=0)
+ |
|
|
3 |
i, |
(k =1) |
|
2 |
|
|||||
|
|
|
|
|
||
|
|
|
|
|
|
|
- |
|
3 |
|
і, |
(k = 2) |
|
|
2 |
|
||||
|
|
|
|
|
||
2.2 Основні елементарні функції комплексної змінної
Показникова функція ez обчислюється за допомогою формули Ейлера:
ez = ex+iy = ex(cos y + isin y)
Тригонометричні функції sinz i cosz можна обчислити за формулами
sin z = |
eiz − e−iz |
, |
cos z = |
eiz + e−iz |
||||
|
2i |
|
|
|
||||
|
|
|
2 |
|
||||
Функції tgz i ctgz визначаються рівностями |
||||||||
tg z = |
sin z |
, |
|
ctg z = |
cos z |
|
||
|
|
sin z |
||||||
|
|
cos z |
|
|
|
|||
Для тригонометричних функцій залишаються вірними всі формули тригонометрії.
Гіперболічні функції визначаються рівностями
sh z = |
ez − e−z |
ch z = |
ez + e−z |
|
2 |
2 |
|||
|
|
PDF created with pdfFactory Pro trial version www.pdffactory.com

|
|
24 |
|
|
th z = |
sh z |
cth z = |
ch z |
|
ch z |
sh z |
|||
|
|
Логарифмічна функція Ln z , де z ¹ 0 , визначається як функція, обернена до показникової
Ln z = ln |
|
z |
|
+ i(arg z + 2kπ ), |
k = 0;±1;± 2;... |
|
|
||||
Обернені тригонометричні функції |
Arcsin z , Arccos z , Arctg z , |
||||
Arcctg z визначаються як функції, обернені відповідно до функцій sin w,cos w, tg w,ctg w .
Наприклад, якщо z = sin w , то w називається арксинусом числа z і позначається w = Arcsin z .
Ці функції багатозначні і їх можна виразити через логарифмічну функцію
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Arcsin z = -iLn(iz + |
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1- z2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Arccosz = -iLn(z + |
|
|
|
|
|
|
|
|
) |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 -1 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Arctgz = - |
i |
|
Ln |
1+ iz |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1- iz |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Arcctgz = - |
i |
Ln |
z + i |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
z - i |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Загальна |
степенева |
функція |
w = za , де |
|
|
|
|
|
|
a =α + βi – |
будь-яке |
||||||||||||||||||||||||||||||||||||||
комплексне число, визначається рівністю |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
za = ea Ln z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Якщо a = |
|
|
, nÎ N , |
то маємо |
багатозначну |
функцію |
– корінь |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
степеня n з комплексного числа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arg z +2kπ |
|
|
|
|
||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Ln z |
|
1 |
(ln |
|
|
z |
|
+i(arg z +2kπ )) |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
||||||||||
zn = n z = en |
= en |
|
|
|
|
|
|
|
|
|
|
|
|
= n |
|
z |
e |
|
|
|
n = |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
æ |
|
arg z + 2kπ |
|
|
|
|
|
|
|
arg z + 2kπ ö |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
= n |
|
z |
|
|
|
|
|
+ i sin |
|
|
k = 0, n |
-1 |
|||||||||||||||||||||||||||||||||||||
|
|
|
çcos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷, |
|
|
||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Загальна показникова функція w = a z |
|
( a ¹ 0 – будь-яке комплексне |
|||||||||||||||||||||||||||||||||||||||||||||||
число) визначається рівністю |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
PDF created with pdfFactory Pro trial version www.pdffactory.com

25
w = az = ez Ln a
Приклад 2.5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ -1- i ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Обчислити а) Lnç |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
2 |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Розв’язок |
|
|
|
|
|
|
|
|
|
б) Arccos 2i |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
а) За означенням |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Ln z = ln |
|
z |
|
|
+ i(arg z + 2kπ ), k = 0, ±1, ± 2,... |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
-1- i |
|
|
|
|
æ |
|
|
1 ö2 |
æ |
|
|
1 |
|
ö2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
= |
|
ç |
- |
|
|
|
÷ |
+ ç- |
|
|
|
|
÷ =1 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 |
|
|
|
|
|
è |
|
|
2 ø |
è |
|
|
2 |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
- |
|
1 |
ö |
|
|
|
|
|
|
|||||
æ |
-1- i ö |
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
÷ |
|
|
|
π |
|
3π |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ç |
|
|
|
|
2 |
|
÷ |
|
|
|
|
|||||||||||||||||||||
|
argç |
|
|
|
|
|
|
|
|
÷ |
= -π + arctg |
|
|
|
1 |
÷ |
= -π + arctg1 = -π + |
4 |
= - |
4 |
||||||||||||||||||||
è |
|
|
2 |
|
ø |
|
|
|
|
|
|
|
|
ç |
|
- |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
÷ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
ø |
|
|
|
|
|
|
|||||
æ |
-1- i ö |
|
|
|
æ |
|
|
3π |
|
+ 2kπ |
ö |
πi |
(8k - 3), k = 0, |
|
|
|
||||||||||||||||||||||||
|
Lnç |
|
|
|
|
|
|
|
|
÷ |
= ln1 |
+ iç |
- |
|
|
|
|
÷ = |
|
±1, ± 2,... |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
||||||||||||||||||||||||||||
è |
|
|
2 |
|
ø |
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|||||||||||||||
б) Arccos z = -i Ln(z + |
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
z2 -1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Тоді Arccos2i = -i Ln(2i + |
|
|
|
|
)= -i Ln(2i + |
|
|
) |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
(2i)2 -1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
- 5 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Тому що |
|
|
|
|
|
|
= ± |
|
|
|
|
i , отримаємо Arccos 2i = -i Ln(2 ± |
|
|
)i |
|||||||||||||||||||||||||||||
|
|
|
|
- 5 |
5 |
|
5 |
|||||||||||||||||||||||||||||||||||||
|
|
(2 + |
|
)i |
|
= 2 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
5 |
|
5, |
|
(2 - 5)i |
= 5 - 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
arg(2 + |
|
)i = π , |
|
|
|
|
|
arg(2 - |
|
)i = - π |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
5 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
2 |
|
|
|
|
π |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
ö |
|
|
|
|
|
|
|
i(4k ±1) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Ln(2 ± 5)i = ln( 5 ± 2)+ iç± |
2 |
+ 2kπ ÷ = ln( 5 ± 2)+ |
2 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
ö |
π |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
± 2) |
+ |
|
|
|
|
(4k |
±1)- i ln( 5 ± 2), |
|||||||||||||||||||||||||
|
|
Arccos 2i = -içln( 5 |
2 |
i(4k ±1)÷ = |
2 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
k = 0, ±1, ± 2,...
PDF created with pdfFactory Pro trial version www.pdffactory.com
26
2.3 Аналітичні функції
Похідною функції комплексної змінної w = f (z) |
називається границя |
||||||
|
w |
= lim |
f (z + z) − f (z) |
= |
′ |
|
|
lim |
|
|
f (z) |
при умові, |
|||
z |
z |
||||||
z→0 |
z→0 |
|
|
|
|||
що z прямує до 0 довільним чином.
Функція називається диференційовною в точці z, якщо існує похідна в цій точці. Якщо функція диференційовна як в самій точці z, так і в деякому її околі, то функція називається аналітичною в точці z.
Функція f(z), що однозначна та диференційовна в кожній точці області
D, називається аналітичною в області D.
Для того, |
щоб функція f (z) = u(x, y) + iv(x, y) була аналітичною в |
області D, необхідно і достатньо існування в цій області неперервних |
|
частинних |
похідних u(x, y) і v(x, y) , що задовольняють умовам |
Коші-Рімана: |
|
|
ì¶u |
|
|
¶v |
|
|
|
|
|
||||||
|
|
|
|
|
= |
|
|
|
|
|
|||||||
|
|
|
|
|
ï |
¶x |
¶y |
|
|
|
|
|
|||||
|
|
|
|
|
ï |
|
|
, |
|
|
|
|
|||||
|
|
|
|
|
í |
¶u |
= - ¶v |
|
|
|
|
||||||
|
|
|
|
|
ï |
|
|
|
|
|
|||||||
|
|
|
|
|
ï |
¶y |
|
|
|
¶x |
|
|
|
|
|
||
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
||||
|
|
¢ |
¶u ¶v ¶u ¶u ¶v ¶u ¶v ¶v |
||||||||||||||
та при цьому f (z) = |
|
+i |
¶x = |
|
-i |
|
|
= |
¶y -i |
|
= ¶y +i |
¶x . |
|||||
¶x |
¶x |
¶y |
¶y |
||||||||||||||
Приклад 2.6 |
|
|
|
|
|
f (z) = u(x, y) + iv(x, y) |
|
||||||||||
Знайти аналітичну |
функцію |
|
|
по відомій |
|||||||||||||
уявній частині v(x, y) = 3x + 4yx . |
|
|
|
|
|
|
|
|
|||||||||
Розв’язок |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Використаємо умови Коші-Рімана: |
|
|
|
|
|
|
|
|
|||||||||
∂u |
= ∂v = |
∂(3x + 4yx) = 4x |
|
|
|
|
|
|
|
|
|
|
|
|
|||
¶x |
¶y |
¶y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
= - ∂v |
= - ∂(3x + 4yx) |
= -3 - 4y |
|
|
|
|
|
|||||||||
¶y |
¶x |
¶x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Проінтегруємо перше з відношень по х. u(x, y) = ò4xdx +ϕ( y) = 2x2 +ϕ(y)
PDF created with pdfFactory Pro trial version www.pdffactory.com

27
Для знаходження функції ϕ( y) продиференціюємо отриману рівність по у і підставимо в другу умову Коші-Рімана
|
∂u |
¢ |
¢ |
- 4y |
|
|
|
|
|
|
|
|
|||
|
¶y = ϕ ( y), |
ϕ ( y) = -3 |
|
|
|||
ϕ( y) = ò(-3 - 4y)dy = -3y - 2y2 + C , де C – const. |
|
||||||
Таким |
чином, |
дійсна |
частина |
невідомої |
функції |
||
u(x, y) = 2x2 - 3y - 2y2 + C. |
|
|
|
||||
Тоді f (z) = u + iv = 2x2 - 3y - 2y2 + C + i(3x + 4yx) = |
|
||||||
|
= 3i(x + iy) + 2(x2 - y2 + 2ixy) + C = 3iz + 2z2 + C |
|
|||||
2.4 Інтегрування функції комплексної змінної
Нехай функція f (z) визначена і неперервна в області D, а L –
кусково-гладка замкнена або незамкнена крива, що належить області D.
Якщо z = x + iy , f (z) = u(x, y) + iv(x, y) , то обчислення інтеграла зводиться до обчислення двох криволінійних інтегралів другого роду
ò f (z)dz = òudx - vdy + iòvdx + udy
L L L
Звідки випливає, що взагалі інтеграл ò f (z)dz залежить від лінії
L
інтегрування L.
Приклад 2.7
Обчислити інтеграл ò(2z + Im z2 )dz
L
а) по прямій у=х від точки z1 = 0 до точки z2 =1+ i
б) по параболі y = x2 від точки z1 = 0 до точки z2 =1+ i .
Розв’язок:
Знайдемо дійсну та уявну частини підінтегральної функції: f (z) = 2z + Im z2 = 2(x - iy) + Im(x2 - y2 + 2ixy) = 2x + 2xy - i × 2y
PDF created with pdfFactory Pro trial version www.pdffactory.com
28
u(x, y) = 2x(1+ y) v(x, y) = −2y
ò f (z)dz = ò2x(1+ y)dx + 2ydy + iò- 2ydx + 2x(1+ y)dy
L L L
а) L – пряма у=х, dy=dx, x змінюється від 0 до 1.
ò f (z)dz = ò1 (2x(1+ x)+ 2x)dx + iò1 (- 2x + 2x(1+ x))dx =
L |
0 |
|
|
|
|
0 |
|
|
|
|
|
|
= ò1 (2x2 + 4x)dx + iò1 2x2dx = |
8 |
+ |
2 |
i |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
0 |
|
0 |
3 |
|
3 |
|
|
|
|
|
|
|
б) L – парабола y = x2 , dy=2xdx, х змінюється від 0 до 1. |
|
|
||||||||||
ò f (z)dz = ò1 (2x(1+ x2 )+ 2x2 ×2x)dx + iò1 (- 2x2 + 2x(1+ x2 )2x)dx = |
|
|||||||||||
L |
0 |
|
|
|
|
|
|
0 |
|
|
|
|
= ò1 (6x3 + 2x)dx + iò1 (4x4 + 2x2 )dx = 5 |
+ 22i |
|
|
|
|
|||||||
0 |
|
0 |
|
|
|
2 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Якщо |
лінія |
L задана |
|
|
|
|
|
ìx = x(t) |
, |
t0 £ t £ t1 |
, |
|
параметрично í |
= y(t) |
|||||||||||
|
|
|
|
|
|
|
|
îy |
|
|
|
|
причому значення параметра t=t0 i t=t1 відповідають початковій та кінцевій точкам кривої L, то
|
|
|
t1 |
|
|
¢ |
де z(t) = x(t) + i y(t) |
||
ò f (z)dz = ò f (z(t))× z (t)dt, |
||||
L |
|
|
t0 |
|
Приклад2.8 |
|
|||
|
òe |
|
dz , де L – відрізок прямої у = –х, який з’єднує точки |
|
Обчислити |
z |
|||
|
L |
|
||
z1 = 0 і z2 = π - iπ .
Розв’язок:
Запишемо рівняння лінії L в параметричній формі x = t, y = −t
PDF created with pdfFactory Pro trial version www.pdffactory.com

29
В комплексно-параметричній формі рівняння прямої буде мати вигляд
z = t − it , де t змінюється від 0 до π . |
|
|
|
|
|||
|
= t + it, |
dz = (1- i)dt |
|
|
|
|
|
z |
|
|
|
|
|||
òez dz = πòet +it (1- i)dt = (1- i)πòe(1+i)t dt = |
1- i |
e(1+i)t |
|
π |
|||
|
|||||||
|
= |
||||||
|
|||||||
L |
0 |
0 |
1+ i |
|
0 |
||
|
|||||||
= -i(e(1+i)π - e(1+i)0 )= (eπ +1)i
Якщо L – коло або частина кола з центром в точці z0 і радіусом R, то зручно використовувати рівняння виду
Приклад 2.9 |
|
|
z = z0 + Reit |
(0 £ t < 2π ) |
|
||||||||
|
|
|
|
|
|
|
|
||||||
Обчислити ò(2iz + z |
|
)dz , де L – дуга кола |z|=2, |
0 ≤ arg z ≤ π . |
||||||||||
z |
|||||||||||||
|
L |
|
|
|
|
|
|
|
|
||||
Розв’язок: |
|
|
−it |
|
|
|
|
|
|||||
|
it |
|
|
2e |
¢ |
= 2ie |
it |
dt, 0 |
£ t £ π . |
||||
|
|
||||||||||||
Нехай z = 2e , z = |
|
, dz = z (t)dt |
|
||||||||||
Тоді |
ò(2iz + z |
|
)dz = πò(2i × 2eit + 2eit × 2e−it )× 2ieitdt = |
||||||||||
z |
|||||||||||||
|
L |
0 |
|
|
|
|
|
|
|||||
π |
(ie2it + eit )dt = |
(4ie2it + 8eit )π = -16 |
|
|
|
||||||||
= 8i ò |
|
|
|
||||||||||
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Якщо f(z) – аналітична функція в однозв’язній області D, то інтеграл не залежить від лінії інтегрування L.
В цьому випадку |
ò f (z)dz = 0, |
L
де L – будь-який замкнений кусково-гладкий контур в області D. Також, якщо f(z) – аналітична функція, то має місце формула Ньютона-Лейбниця:
zò1 f (z)dz =Ф(z1) -Ф(z0 ) , z0
PDF created with pdfFactory Pro trial version www.pdffactory.com

30
де Ф(z) – первісна до функції f(z), тобто Ф′(z) = f (z) в області D, z0 , z1 D .
Приклад 2.10
Обчислити інтеграл òcos zdz , де L – відрізок прямої, що з’єднує
L
точки z1 = π2 і z2 = π + i .
Розв’язок:
Підінтегральна функція f(z)=cosz аналітична всюди, тому застосовуємо формулу Ньютона-Лейбниця:
π +i |
|
ππ+i = sin(π + i) - sin |
π |
|
òcos zdz = sin z |
|
= -sin i -1 = -(1+ ish1) |
||
|
||||
π |
|
2 |
2 |
|
2 |
|
|
|
|
Якщо f(z) іϕ(z) – аналітичні функції в однозв’язній області D, а z0, z1
– довільні точки цієї області, то має місце формула інтегрування частинами:
z1 |
|
|
(z)dz = ( f (z) |
×ϕ(z)) |
|
z1 |
z1 |
|
|
|
|
||
ò |
f (z) ×ϕ |
¢ |
|
- ò |
¢ |
|
|
|
|||||
|
|
||||||||||||
|
|
z0 |
ϕ(z) × f (z)dz |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
z0 |
|
|
|
|
|
|
|
|
z0 |
|
|
|
|
Приклад 2.11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Обчислити інтеграл òi z cos zdz |
|
|
|
|
|
|
|
|
|||||
Розв’язок: |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
ϕ(z) = cos z |
|
|
|
|
|
|
|
|
|||
Функції f(z)=z і |
|
всюди |
аналітичні, тому можна |
||||||||||
проінтегрувати частинами: |
|
|
|
|
|
|
|
|
|||||
i |
i |
|
′dz = (z sin z) |
|
i |
i |
|
|
|
i |
|
||
ò z cos zdz = |
ò z(sin z) |
|
− ò sin zdz = i sin i + cos z |
|
= |
||||||||
0 |
0 |
|
|
|
0 |
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
= −sh1+ ch1−1 = 1−e e .
PDF created with pdfFactory Pro trial version www.pdffactory.com
