31. Геометрические приложения опред инт

Вычисление площадей плоских фигур. Пусть D – ограниченная фигура в плоскости Oxy и D – ее площадь. Тогда в зависимости от описания этой фигуры различают следующие применения ОИпри вычислении площади:

а) в декартовых координатах:

1.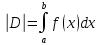, если D– криволинейная трапеция, ограниченная снизу осью Ox, сверху – графиком неотрицательной функцииy   f  (х), а с боков – прямымиx  a и x   b (a b).

2. 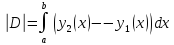,если D – фигура, ограниченная снизуграфиком функции y = y1(х), сверху – графиком функции y = y2 (х), где y2(x) ≥ y1(x), x∈[a, b],и с боков – прямымиx a и x b (a b).

3. 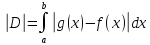, если D – фигура, ограниченная сверхуи снизу графиками функций y f(х), y g(х) и с боков – прямымиx a и x b.

б) в случае параметрического задания:

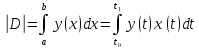, если D – криволинейная трапеция,ограниченная линией 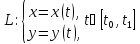,заданной параметрически и .

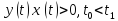в)в полярных координатах x = r cosϕ, y = r sinϕ:

используя метод дифференциалов, получаем:

1.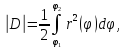если D – криволинейный сектор, ограниченный лучами ϕ = ϕ1, 2 ϕ = ϕ и кривой r = r(ϕ), ϕ∈[ϕ1,ϕ2 ].

2. 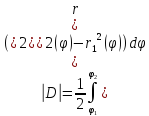, если D − фигура, ограниченная лучами ϕ = ϕ1, 2 ϕ = ϕ и кривыми r = r1(ϕ), r = r2 (ϕ), ϕ∈[ϕ1, ϕ2].

Вычисление длины дуги плоской кривой. Под длиной s дуги кривой понимают предел вписанных в эту дугу длин ломаных, когда наибольшая из длин звеньев ломаных стремится к нулю. Будем рассматривать так называемые спрямляемые кривые, т. е. кривые, для которых длина бесконечно малой дуги кривой эквивалентна длине стягивающей дугу хорды. Для таких кривых Δs ≈ (Δx)2 + (Δy)2 или, переходя к дифференциалам, ds(dx)2 (dy)2 или (ds)2 (dx)2 (dy)2, что иногда называют «теоремой Пифагора» для дифференциалов.

1. Если рассматриваемая кривая L задана параметрически, т. е.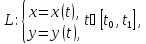и являетсягладкой, т. е. функции x(t), y(t)непрерывно дифференцируемы и их производные одновременно в нуль не обращаются, то можно получить формулу для вычислений длины s_L гладкой параметризованной кривой L:

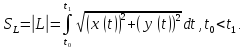
2. Если кривая L задана явно как график функции y y(х), x ∈ [a, b], то формула для вычисления длины дуги кривой упрощается (здесь t = x):

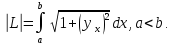
3. Аналогично можно рассмотреть выражение для нахождения дуги в полярных координатах, если в качестве параметра t принять полярный угол ϕ.

32. приблеженное вычисл опред инт Рассмотр. Задачу: выч. С точностью до 0.01 интег. .Геом. — это означает, что надо найти площадь криволин.трапеции огрн. Гр ф-и сверху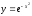по бокамX=0, X=1

Формула прямоугольников (средних прямоуг)

для вычисл. 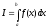разбивают отрезок [a;b] наn равных отрезков длины h

h=(b-a)/n

x₀=a x_i=x₀+ih, 1≤i≥n

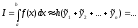
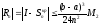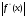, где M₂=max x принадл.[a;b]

Формула трап.получается при замене S кривол. трап на S обыч. трап

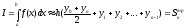
Формула парабал(формула Симпсона)

При замене на каждом частях отрезке граф ф-у f(x) параболой

При этом [a;b] разбивают на h=(b-a)/2n

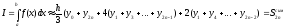
где M₄=max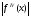 x принадл.[a;b]

Формула трапеций

Получ.при замене на каждом частях отр.S крив.трапеции S обыч.трапеции

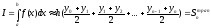
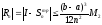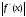,где M₂=max x принадл.[a;b]

33. Понятие ду его общего и частного решений. Задача Коши. Теорема сущ и единственности решения задачи Коши.

ДУ наз ур-ние вида F(x,y’,y’’…yⁿ), связыв. незов перем х, искомую ф. у, завис. от этой перем. и производную. Процесс нахождения реш ДУ наз интегриров ДУ. График ДУ наз диф кривой. В общ случае решением ДУ n-го порядка опред с точностью до n произвольных постоянных.

Общим реш ДУ n-го порядка наз ф y= ϕ (x,c₁, c₂…c_n) завис от n-произв пост и удовлетв усл: явл реш данного ДУ при любых знач произвольных пост c₁, c₂…c_n ; каковы бы не были нач усливия, y(x₀)=y₀, y’(x₀)=y_0,1 , y^n-1(x₀)=y_0,n-1 Сущ такие знач произв пост с₁=с₁⁰, с₂=с₂⁰…… с_n=с_n⁰ , что ф у= ϕ ( x; с₁⁰; с₂⁰…..с_n⁰) удовл данному ДУ и ук нач усл.

Частным реш ДУ наз ф у= ϕ (x; с₁⁰; с₂⁰…..с_n⁰), кот получ из общ реш при конкрет знач произв пост Если общ реш ДУ найдено в неявном виде Ф(x, у,c₁, c₂…c_n) =0, то говорят, что найден общ инт ДУ.

Задача отыскания реш ДУ удовл нач усл назыв задачей Коши.

Т. Сущ един реш зад Коши для ДУ 1-го пор-ка. Если ф f(x,y) и её f_у’(x,y)- частн произв непрер в некот обл D содерж точ с коорд (x₀,y₀), то сущ единств реш задачи Коши.

Т. Сущ и единственности, реш зад Коши для ДУ 2 пор-ка. Если f(x,y,y’) и её частн производ f_у’(x,y, y’) f_у’’(x,y, y’) в некот т (x₀,y₀, y₀’), то суще ед реш зад Коши

Если в т. М₀(х₀,у₀) наруш хотя бы одно усл т Коши, то эта точка наз особой т соотв ДУ

34. Основные типы ДУ 1-го порядка и методы их решения Типы ДУ первого порядка и методы их решения 1)ДУ с раздел. перем.: y’=f₁(x)*f₂(x)

dy/dx= f₁(x)*f₂(x)

dy= f₁(x)*f₂(x)*dx

ʃdy/f₂(x)= ʃf₁(x)*dx–ДУ с РП