15.Алгоритм нахождения наибольшего и наименьшего значений функции двух переменных в области.

Для ф.н.п как и для ф 1 пер справедлива т Веййер –Штрассе.

Если ф.н.п непрерывна замкн огр области, то она ограниченна в этой области и достиг в ней наиб и наим зним в этой обл значений

Эти значения могут достигаться либо в крит т внутри обл. либо на границе обл.

АЛГОРИТМ НАХОЖДЕНИЯ НАИБ И НАИМ ЗНАЧ

Непрер ф z=f(x,y) в огр области D:

1)найти частные производные.Прировнять их к нулю, найти крит т.

2)выбрать те крит т,которые лежат внутри обл.

3)Найти наиб и наим знач функции на границах области

4)Вычислить знач ф во всех найд т. Выбрать наиб и наим знач

16.Первообразная и неопределённый интеграл.Основные свойства неопределённого интеграла.

F(x) наз первообразной для F(x) на нек промежутке,если для всех x из этого промежутка если F’(x)=F(x)

Т. Если F₁(x) и F₂(x) две различ первообразные ф для F(x) на нек промежутке, то F₁ (x)=F₂(x)+c для всех x из этого промежутка,где с-число.

Основные свойства неопред интеграла

1)( f(x) dx )’=f(x)

d(F(x)dx)=F(x)dx

2)dF(x)=F(x)+c

3) k f(x)dx = k f(x)dx , k=0

4)(f(x)+- g(x))dx =  f(x)dx +- g(x) dx

5)Любая ф-ия интегрирования сохр.свой вид если переменную интегрирования заменить любой диф-ой ф-ей

 f(x)dx =F(x)+c =>f(u)du = F(u)+c

17.Интегрирование по частям и заменой переменной в неопределённом интеграле.Примеры подстановок

Интегрирование по частям

(uv)’=u’v+uv’

(uv)’dx =  u’v dx +  uv’ dx

Uv+c=v du +u dv

u dv = uv -v du

Для применения этой формулы подынтегральное выр предст в виде произведения ф и диф dv. При перех к правой части du=u’dx v=dv

После 2-кратного прим интеграла по частям в первых двух интегр оба раза за и обознач ф одного типа

Интегр выраж из получ выражения

После однократного прим ф-мы интегр по частям и преобр исходный интеграл выраж из исходного ур-ния.

18.Интегрирование простейших рациональных дробей

Рациональной функцией или р.дробью наз ф.вида R(x)=Pn(x)/Qm(x),где Pn(x),Q(m) многочлены

Рац дробь называется правильной если степень числителя меньше знаменателя (n<m), если n>=m неправильная рациональная дробь

Простейшими или элементарными дробями наз правильные дроби след типоп:

1)A/x-a

2)A/(x-a)^k , Kпренадлежит N , K>=2

3)Mx+N/x²+px+g D=p²-4q=0

4)Mx+N/(x²+px+g) D=p²-4g=0 Kпреналеж N,K>=2

Одним из способов подходит инт вида Mx+N/x²+px+g dx* Mx+N/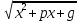 dx*Mx+N/ax²+bx+c dx *

Mx+N/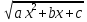dx =>явл выделение полного квадрата с пом замены t=x+b/2a

19.Алгоритм интегрирования рациональных дробей.

1)Если дробь неправильная (n>=m) выделить целую часть дроби разделив числитель на знаменатель про правилу деления многочленов уголком

2)Знаменатель правильной рациональной дроби разлодить на мн и квадр множители

Из осн т алгебры? Следует ,что всякий многочлен степени m имеет ровно m корней с учётом их кратности .Если -действ.корень лич? Кратности r ,то многочлены делятся на (x-)^r

Если многочлен с действ коэфиц. имеет комплексный корень =U+iV кратности r и =u-iv- кр r такие явл компл? Корнями причём многочлен в этом случае делится на ((x-)(-))^r=(x²-2ux+u+v²)^r

3)Т разложить прав рац дробь на сумму простейших дробей

Т.Всякую прав рац дробь со сзнаком (1) моно ед.обр разлодить на суммупрост дробей

4)найти коэф разложения (2)

5)Проинтегрировать получ сумму