11. Частные и полное приращение функции нескольких переменных. Дифференциал функции нескольких переменных

Пусть функция z=f(x, y) определена в некотором окрестности точки М₀ (х₀, у₀), полным приращением функции z=f(x, y) в точке (х₀, у₀) отвечающим приращением аргумента х и у называется z=f(x₀+x; y₀+y)-f(x₀, y₀)

Частные приращения

По Х

_хZ = f(x₀+x, y₀) - f(x₀, y₀)

По У

_yZ = f(x₀, y₀+y) - f(x₀, y₀)

12.Правило дифференцирования сложной функции нескольких переменных. Производные неявно заданной функции

((((((Правило диф-ния ф н.н

Производная смешанной функции по незов перем равна сумме произв. частных произв по промежут аргументом на произв этих аргументов по независимой переменной.

Т.Если ф u=u(x) и v=v(x) диф-мы в т. X₀ .ф. y=y(u,v) диф-ма в т. (U_0,V₀ ) причём U(x₀)=u₀ V(x₀)=V₀

То y=y(u(x),v(x)) в т. X₀ диф-ма и справедлива формула

dy/dx =)))))))

Производная сложной функции по независимой переменной = сумме произведений частных производных по промежуточным аргументам на произв этих аргументов по независ пер.

Теорема: Если ф-ии U=U(x) и V=V(x) диф. В т. X₀ ф-ия y=(u,v) диф в точке U₀ , V₀ , причём U(x₀)=U₀

V(x₀)=V₀ то сложная функция y=y(u(x)’,V(x)) диф в.т.X₀ и dy/dx=∂y/∂x*du/dx+∂y/∂v*dv/dx

Доказательство dy/dx=lim при x0 y/x

13.Линия уровня, градиент и производная по направлению функции двух переменных. Свойства градиента.

Частная производная ф.2 пер характер. скорость изменения ф при изменении только одной перем т.е движение вдоль коорд. осей

Для характеристики скорости изм ф. в направлении заданного вектора вводится понятие произв по направлению.

Произв ф z=F(x,y) т M₀ (x₀ ,y₀) по напр. вектора наз предел, если он сущ и конечен, отношения приращения ф. в данном напр к величине перемещения при условии, что величина перем 0.

∂z/∂e=lim_l0 _l z/l

Производная по направлению характеризует скорость функции по направлению.

Градиент ф.н.п наз вектор, координаты которого равны соотв частым производным

U=u(x,y,z),то u = ∂u/∂z*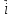+∂u/∂y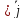+∂u/∂z*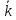

Свойства:

1. ∂u/∂l=∂u/∂x cos + ∂u/∂y cos + ∂u/∂z cos

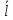∂u/∂l=u*,где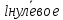

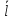
|l⁰|=1

∂u/∂l = || |e⁰ | cos  , где  = (,u

∂u/∂l = | u| cos 

2. Следовательно произв по напр имеет наиб знач (при cos  = 1) т.е в напр градиента и причём ∂u/∂l =

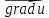= || если 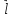

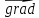
3)градиент хранит напр наискорейшего возр ф

4)Градиент перпендикул поверхности уровня (для ф 2 линии уровня ) проведённой в данной точке

14 Экстремумы функции двух переменных. Необходимое и достаточное условия существования экстремума.

ф z=z(x,y) имеет в т M₀ (x₀ ,y₀) глоб max (min) в обл X , если z(x_0, y₀) > z(x,y)

для всех т.M(x,y)пренадлеж X )……

т.1 необходим условие сущ лок экстр ф.н.п если т.(x_{0 ,} y₀ ) явл т.лок экстр ф.

z = z (x,y),

то

{_{z’y(x(0),y(0))=0}^{z’x(x(0),y(o))=0 //система} _ур

_{или хотя бы одна из них не сущ}

_{т.в которой произв = 0 или не сущ,то они наз критичными или стационарными}

_{Т.2 дост усл лок экстр диф-ой ф.2.п}

_{Пусть (x0,y0)-критич точка диф.ф z=z(x,y) и пусть ф. z=z(x,y) имеет в нём окр этой точки непрер частные производные 2-го порядка}

_{0=|Z’’xx(x0,y0) z’’xy(x0,y0)|}

_{|z’’xy (x0,y0) z’’yy(x0,y0)|}

_{составим определитель}

_тогда:

1. _{>0 ,z’’xx(x0,y0)>0 т. т (x0,y0)-т лок min}

2. _{>0, z’’xx(x0,y0) то т.(x0,y0)-т лок max}

3. _{<0, то т.(x0,y0) не явл т лок экстр}

4. _{i =0 ,то доп исследования}