20.Универсальная тригонометрическая подстановка.

T=tg x/2

Замечание:удобно исп универс тригоном подст для нахожд dx/sinx :dx/cosx

21.Интегралы вида sin^m cosⁿ xdx,где m и n-целые числа

.Интегралы вида sin^m cosⁿ xdx, m,n пренадлеж z, m,n>=0

Если m=2k+1 (нечётное) ,то t=cos x

Если n=2k+1 (нечётное) ,то t=sin x

m=2k,n=2k (чётное) то исп ф понижения степени

cos²x=(1-cos2x)/2

sin²x= 1-cos2x/2

22. Интеграл вида x=t^s , где s- наим. общий знаменатель степеней

23.Интегралы вида

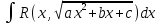
Выделяется полный квадрат и если то x=a*sin(t) или x=a*cos(t)

Если 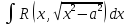то x=a/cos(t) или x=a/sin(t)

Если 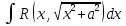то x=a*tg(t) или x=a*ctg(t)

24.Понятия и примеры неберущихся интегралов.

xe^{-x^2}dx

Т.Коши?: всякие ? непрерыв на [a;b] функция f(x) имеет первообразную F(X) явл элементарный функцией .Если первообразная ф f(x) не явл эл ф,то говорят,что f(x)dx не выраж через элементарные ф или что он не берущийся.

Другие примеры не берущихся интегралов

e^{-x^2}dx-инт Пуассона

cos x² dx – интеграл Френеля

25. Понятие определенного интеграла, его геом. Смысл. Условия интегрируемости функций.

Если сущ. предел (и конечен) интегр-ия сумм (Lim Sn) при измельчении изменения d_n->0 незовисимой ни от способа разбиения отр [a;b] на частичные отрезки, ни от выбора с, то этот предел наз определенным интегралом от f(x)по отрезку

Геом. Смысл: опред интеграл от неотрицат на отр [a;b]ф f(x) выражает площадь криволинейной трапеции. Ограниченной сверху y=f(x), сбоку [a;b] и снизу ОХ

Условия интегрируемости: необх условие: если f(x) интегр-ма на отр [a;b] то она определена на этом отрезке

Дост усл игтегри-сти: если f(x) непр-вна на [a;b] то она интегрируема на этом отрезке

Если f(x) определена на [a;b]и непрер на нем везде, кроме конечного числа точек разрыва 1 рода то она интегрируема на [a;b]

26. Основные свойства определенного интеграла. Оценки интегралов. Теорема о среднем значении знач функции на отрезке.

Св-ва: 2)

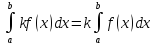
Оценки интегралов: если f(x)≥0 на отр [a;b] то

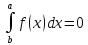
Если f(x)≥g(x) на [a;b] то ;

Если f(x) интегр(ограничена) на [a;b] m и M – наиб и наим знач ф на [a;b] m(b-а)≤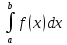≤M(b-a)

т.к

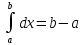
теорема о среднем: Если f(x)непрер на [a;b] то сущ такая точка «с» на отр, что

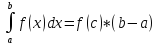
27. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница Пусть f(x) интегр-ма на [a;b] тогда она будет интегр-ма на любом отрезке от а до х, где а≤х≤в следовательно определена следуюзая фуункция Ф(х)=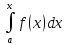 (интеграл с переменным верхним пределом) т. Если f(x) непрер, то сущ производная интеграла от f(x)с переменным по перемменному верхнему пределу и она = значению подинтегральной функции в точке соответствующей верхнему пределу ф.Ньютона- Лейбница:

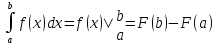
28. Замена переменной и интегрирование по частям в определенном интеграле. Свойства интегралов от четных и нечетных функция по симметричному относительно нуля промежутку. Интегрирование по частям.

=

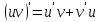
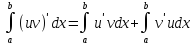
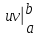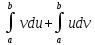
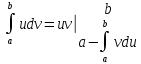
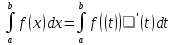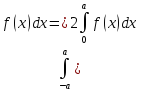Замена переменной в определённом интеграле. Если x=(t) непрерывна и имеет непрерывную производную на отрезке [t₁, t₂], тогда (t₁)=a, (t₂)=b и область значений (t) на отрезке [t₁; t₂] является отрезком [a;b], (x) – непрерывна на [a;b], то Свойства интегралов от четных и нечетных функция по симметричному относительно нуля промежутку: пусть f(x)-четная, т.е f(-x)=f(x) тогда интеграл от еслиf(x)- нечетная, то f(x)=-f(x),