29. Несобств.Инт. С бесконеч. Пределами инт признаки сравнения. Примеры сходящихся и расходящихся инт.

При введение опред. определенного инт. предполагали что 1) пределы интегрирования конечны и подинт. ф-я ограничена на отрезке интегрирования.

Несобств.инт. явл обобщ.понятием определенного интеграла на случ.бесконечного отрезка интегрирования или неогр.ф-и.Основная идея построения несобств.инт.(график)

Отступает от особенности внутрь отрезка интегрирования так, чтобы сущ.опред.инт. и переходит к пределу

Пусть ф-я f(x) опред. и интегрируема на любом отрезке от а до b (b>a). Несобств.инт с бесконеч. верхним пред. интегр. наз. предел: 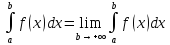причем если этот предел сущ и конечен, то интегрирование наз сходящимся в противном случ сходящимся

ПРИМЕР

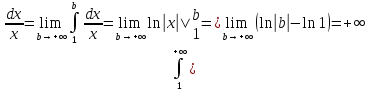
ПРИМЕР

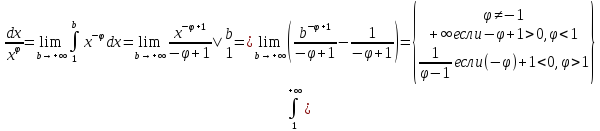
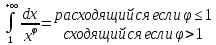
Аналогично определяется несобст.инт с бесконечным нижним пределом

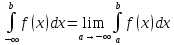
Определённый интеграл 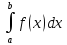называется несобственным, если выполняется, по крайней мере, хотя бы одно из следующих условий:

• Предел a или b (или оба предела) являются бесконечными;

• Функция f (x) имеет одну или несколько точек разрыва внутри интервала [a,b].

Начнем с интегралов по бесконечному промежутку. Пусть I –один из промежутков вида: (−∞, a], [b, + ∞) или(−∞, + ∞).Пусть далее на промежутке I определена функция f (х), которая является интегрируемой на любом конечном промежутке, содержащемся в I.Тогда несобственный интеграл по промежутку I рассчитывается следующим образом:

если предел существует и конечен, в этом случае соответствующий интеграл называется сходящимся; если предел не существует или не является конечным, интеграл считается расходящимся.Если наряду со сходимостью интеграла от функции f (x) по промежутку Iимеет место и сходимость интеграла от модуля этой функции, то такая сходимость называется абсолютной.

30. Несобств инт от неогранич ф-й. Признаки сравнения. Примеры сходящихся и расходящихся инт

Пусть на промежутке I (a, b] или I [a, b) или I [a, b] задана функция f , которая имеет на этих промежутках единственную«особенность» – точку c,в окрестности которой функция не является ограниченной. Точка c a для первого, c b для второго и c∈(a, b)для третьего промежутков. Предположим далее, что функция f интегрируема на любом замкнутом промежутке, целиком лежащем в I. Тогда можно определить несобственные интегралы следующего вида:

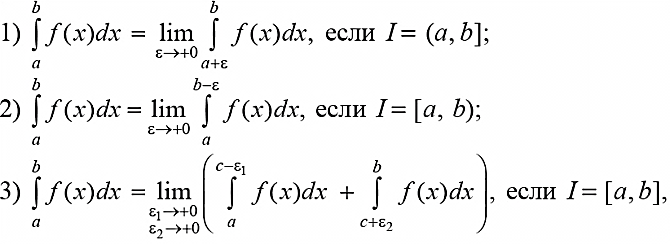
если предел существует и конечен, в этом случае соответствующийинтеграл называется сходящимся; если предел не существует илине является конечным, интеграл считается расходящимся.Если наряду со сходимостью интеграла от функции f (x) попромежутку I имеет место и сходимость интеграла от модуля этойфункции, то такая сходимость называется абсолютной.

Признаки сравнения несобственных интегралов:

1) непредельный: пусть 0 ≤ f (х) ≤ g(х), x ∈ I; тогда

а) если сходится интеграл от функции g(x) по промежутку I, то и сходится и интеграл от функции f (x) по этому промежутку;

б) если же расходится интеграл от функции f (x) по промежутку I, то и расходится и интеграл от функции g(x) по этому промежутку;

2) предельный: если существует конечный отличный от нуля

Предел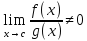гдеc a в случае I (a, b], c b для I [a, b) и c∈(a, b)для I [a, b], то несобственные интегралы отфункций f (x) и g(x) по промежутку Iсходятся (или расходятся)одновременно.

Интеграл вида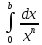часто используется при применении признаков сравнения для несобственных интегралов от неограниченных функций.