1. Возрастание и убывание ф-ции. Условия монотонности дифференцируемой ф-ции на интервале.
Возрастающая
ф-я
– функция y=f(x) возрастает
на интервале X,
если для любых 
и
выполняется
неравенство
.
Другими словами – большему значению
аргумента соответствует большее значение
функции.
Убывающая
ф-я
– Функция y=f(x) убывает
на интервале X,
если для любых 
и
выполняется
неравенство
.
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.
2. Экстремумы функции. Необходимое и достаточные условия существования экстремума.
Экстремум функции - максимальное или минимальное значение функции на заданном множестве.
Функция
z
= z
(x,
y)
в точке
,
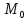
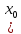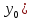глобальнаяmax
(min)
в области х,
если z
(
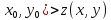для всех точек
M
(x,y)
ϵ x,
если z
(
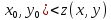для всех точек
M
(x,y)
ϵ x.
Необходимое
условие существования экстремума. Для
Функции нескольких переменных. Если
точки (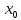
,
)
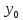является точка локального экстремума
функцииz
= z
(x,
y),
то
(
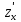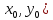=0;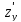
(
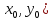=0или хотя бы
одна из них не существует.
Достаточные
условия экстремума. Пусть (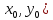
критическая
точка дифференциала функции z=z(x,y)
и пусть функция
z=z(x,y)
в некоторой
окрестности этой точки непрерывные
частные производные 2-ого порядка в этой
точке, тогда
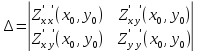
Условия:
1)
,
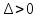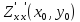>0,
то точка (
)
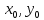– точка локальногоmin
2)
,
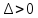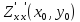<0,
то точка (
)
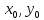– точка локальногоmax
3)
)
,
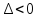то точка (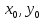
)
– не является точкой локального
экстремума.
4)
,
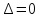то дополнительные исследования.
3. Алгоритм нахождения точек локального экстремума
Условия:
1)
,
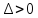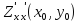>0,
то точка (
)
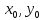– точка локальногоmin
2)
,
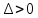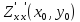<0,
то точка (
)
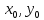– точка локальногоmax
3)
)
,
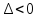то точка (
)
– не является точкой локального
экстремума.
4)
,
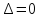то дополнительные исследования.
Непрерывная функция z=f (x, y) в определённой области Д:
Найти частные производные, прировнять их к нулю, найти критические точки.
Выбрать те критические точки, которые лежат внутри области.
Найти наибольшее и наименьшее значение функции на границах области.
Вычислить значение функции во всех найденных точках, выбрать наибольшее и наименьшее значение.
4. Наибольшее и наименьшее значение функции на отрезке.
Непрерывная функция z=f (x, y) в определённой области Д:
Найти частные производные, прировнять их к нулю, найти критические точки.
Выбрать те критические точки, которые лежат внутри области.
Найти наибольшее и наименьшее значение функции на границах области.
Вычислить значение функции во всех найденных точках, выбрать наибольшее и наименьшее значение.
5. Достаточное условие выпуклости графика функции.
1) Если существует f ‘’(x)>0 на (a, b), то график f(x) является выпуклым вниз на (a, b)
2) Если существует f ‘’(x)<0, то график f(x) является выпуклым вверх.
6. Вертикальные, наклонные и горизонтальные асимптоты кривых.
Асимптотой функции y=f(x) называется пряма, обладающая тем свойством, что расстояние от точек графика до этой прямой стремиться к нулю при бесконечном удалении точек графика от начала координат. Различают вертикальные, горизонтальные и наклонные.
Вертикальные. Прямая х=х0 является вертикальной асимптотой графика y=f(x), если функция определена в некоторой точке х0.
Функция может иметь различные наклонные (горизонтальные) асимптоты при х→+∞ и х→ ∞
Горизонтальные асимптоты является частным случаем наклонной (х<0)
Если хотя бы один из пределов не существует или = ∞, то соответствующей наклонной асимптоты не существует.