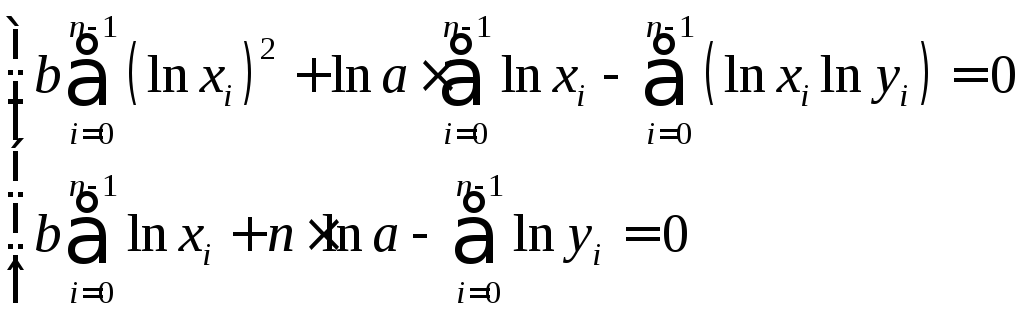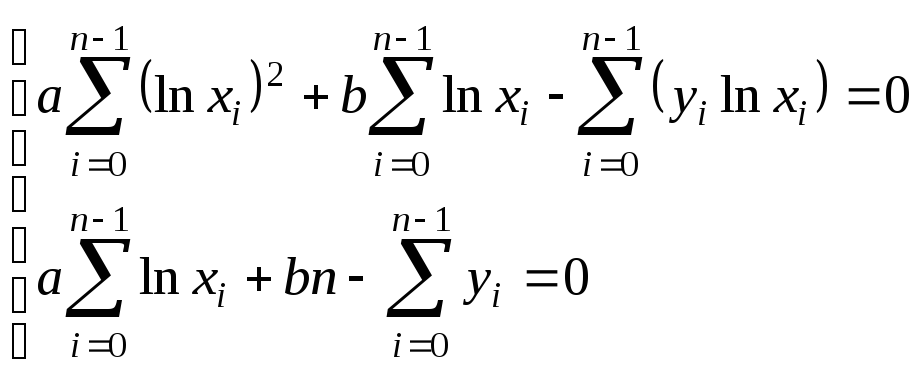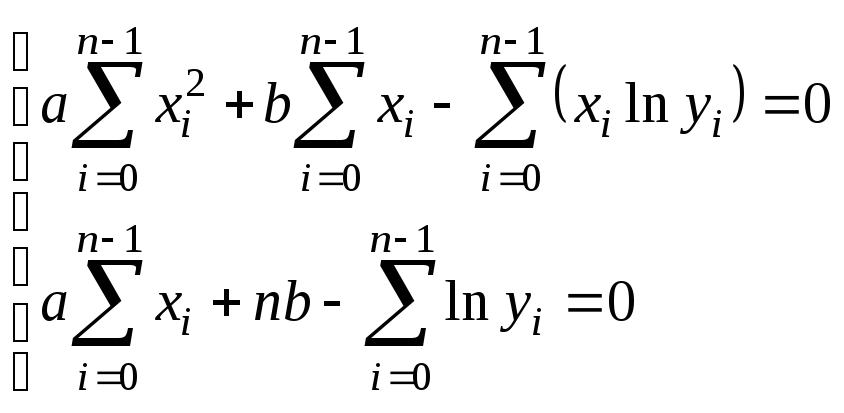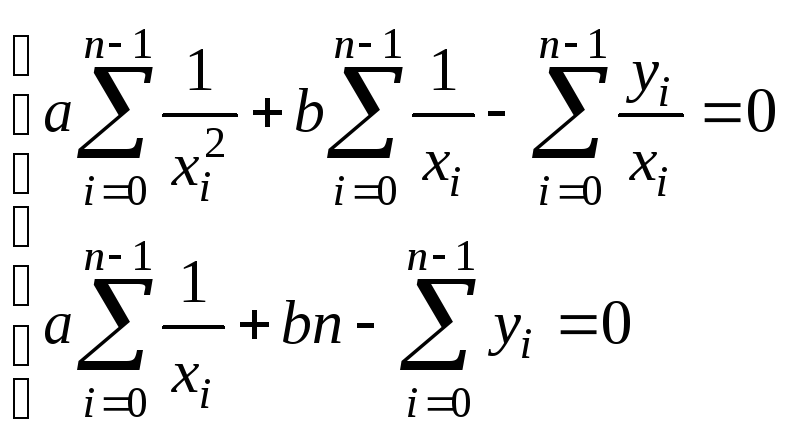3. Лабораторная работа №3. Аппроксимация экспериментальных данных

3.1. Основные теоретические положения

Основная задача аппроксимации – построение приближен-ной (аппроксимирующей) функции наиболее близко проходящей около экспериментально полученных точек или заданной непрерывной функции . В общем смысле термином «аппроксимация» называ-ют замену одних математических объектов другими, например, сложных функций более простой функцией или набором простых функций, в том или ином смысле близкими к исходным. Для количественной характеристики близости вводится соответствующая мера расстояния, определяемая через разности . При этом весьма желательно, чтобы аппроксимация была как можно более точной и вычислялась за малое время.

В простейшем случае задача аппроксимации экспери-ментальных данных выглядит следующим образом: через заданные точки на плоскости или вблизи этих точек провести кривую , которая наилучшим образом воспро-изводила бы график исходной экспериментальной законо-мерности, но в то же время была бы нечувствительна к случайным отклонениям измеряемой величины (рис. 3.1).

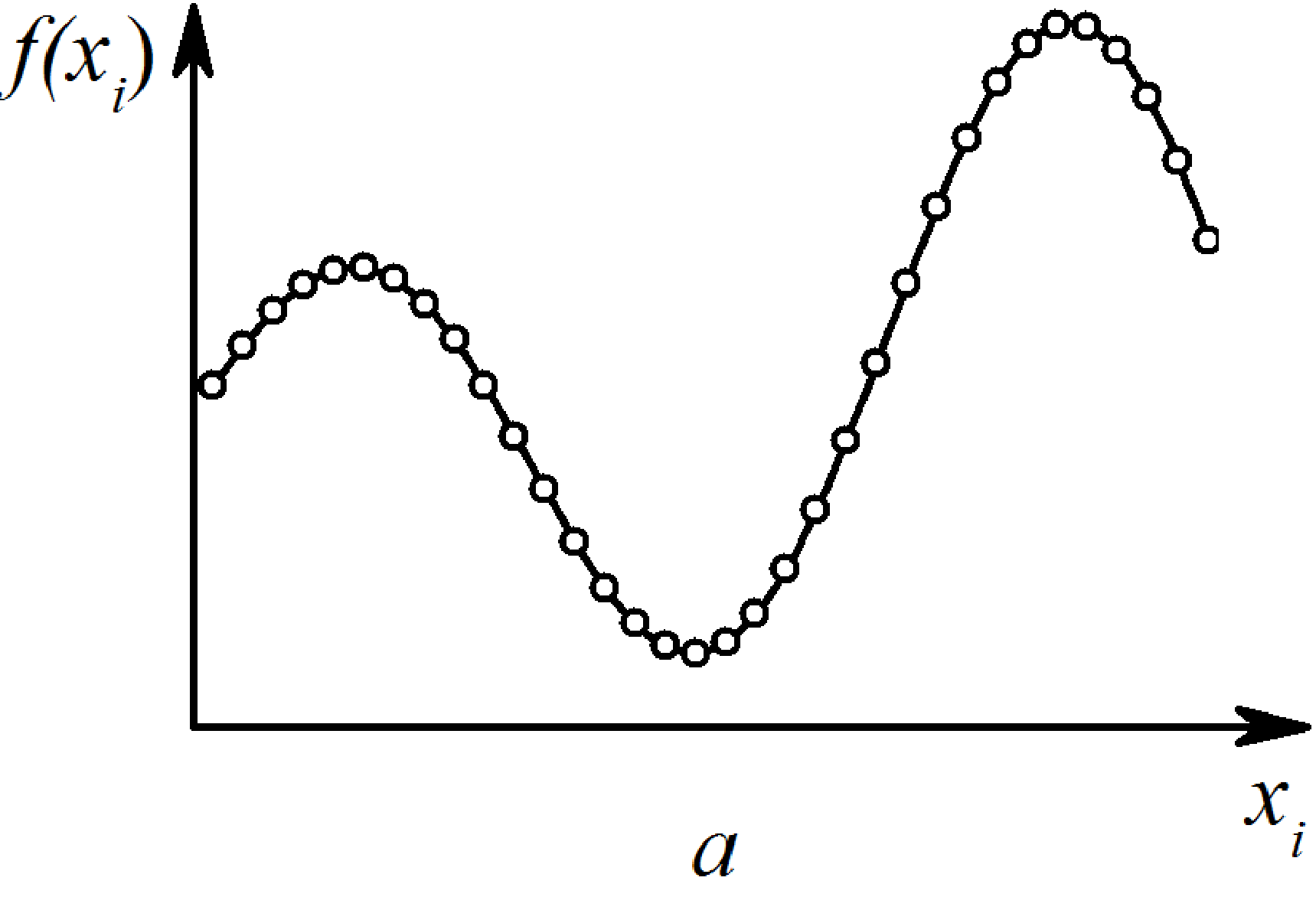
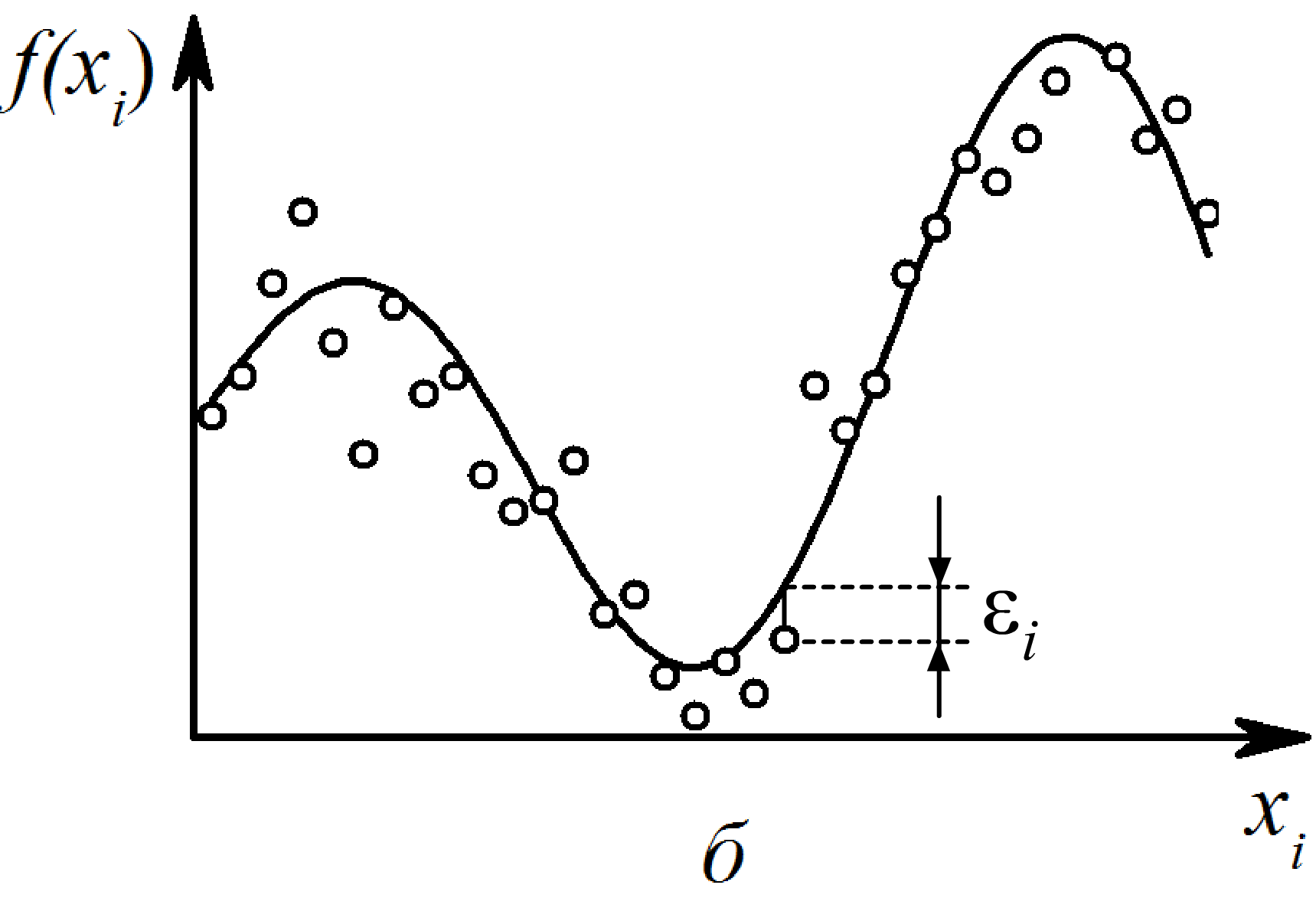
Рис. 3.1. Иллюстрация задачи аппроксимации: а - аппроксимирующая кривая проходит через заданные точки; б - приближенное описание экспериментальной зависимости (точки не ложатся в точности на кривую)

Принято рассматривать эту задачу в двух несколько различных широко распространенных постановках. В первом случае зависимость между величинами и задается заранее известной функцией с точностью до значе-ний параметров . Задача состоит в том, чтобы как можно точнее оценить эти параметры. Важно отметить, что параметры аппроксимации не могут быть непосредственно найдены из эксперимента.

Во второй постановке требуется подобрать функцию соответствующую наилучшему прибли-жению к фактической экспериментальной зависимости . В этом случае непрерывную функцию для аппроксимации дискретной зависимости выбирают из условия наилучшего квадратичного приближения (стандартный метод наименьших квадратов)

. (3.1)

Задачу на поиск минимума можно свести к задаче поиска корня системы уравнений с неизвестными параметрами ,

(3.2)

Подстановка (3.1) в (3.2) приведет к системе алгебраических уравнений (3.3) относительно неизвестных параметров.

Решая эту систему уравнений, найдем значения параметров и, следовательно, искомую аппроксимирующую функцию , удовлетворяющую сформулирован-ным выше требованиям.

(3.3)

Для аппроксимации могут использоваться любые функции, но задача значительно упрощается, когда параметры в аппроксимирующую функцию входят линейно

, (3.4)

где произвольные базисные функции. Общих рекомендаций по выбору базисных функций нет. Выбор класса и задание свойств этих функций должны осуществляться с учетом свойств исследуемых экспериментальных данных. Иначе аппроксимация будет трудоемка и осуществлена недостаточно эффективно. Как правило, разные базисные функции имеют свои преимущества и недостатки, но наилучшей считается аппроксимирующая функция, в которой используется небольшое число базисных функций.

Если , то число коэффициентов аппроксимации недостаточно для правильного воспроизведения графика экспериментальной зависимости, а в случае значительно увеличиваются ошибка оценки и время вычисления параметров, а также усложняется их интерпретация (физический смысл).

Подстановка (3.4) в (3.1), а затем вычисление производных (3.2) приведет в итоге к следующей системе линейных алгебраических уравнений:

(3.5)

Для нахождения неизвестных параметров обычно составляется расширенная матрица, которую называют матрицей Грамма. Элементами этой матрицы являются скалярные произведения базисных функций и столбец свободных коэффициентов:

,

где

.

Основное преимущество рассмотрения матрицы Грамма состоит в том, что для нахождения решения системы (3.5) необходимо сосчитать только элементы первой строки и двух последних столбцов: остальные элементы заполняются сдвигом предшествующей строки (за исключением двух последних столбцов) на одну позицию влево. А в случае ортогональности базисных функций

все недиагональные элементы матрицы Грамма равны нулю, что увеличивает точность вычисления параметров. Хорошо известными системами ортогональных базисных функций являются полиномы Лежандратригонометрические ряды Фурье, вейвлет-функции.

Рассмотрим некоторые примеры аппроксимирующих функций:

1. Полиномиальная аппроксимация.

Аппроксимирующая функция представляет собой полином степени вида

здесь базисные функции представлены в виде последовательности степеней аргумента :

Система уравнений линейных алгебраических уравнений для параметров выглядит следующим образом

Расширенная матрица Грамма для степенного базиса имеет вид:

.

Вычисляя все входящие в матрицу суммы по экспериментальным данным, параметры могут быть найдены, например, методом Гаусса.

В частности, если аппроксимирующая функция является линейной

с базисными функциями для которых скалярные произведения соответственно равны

расширенная матрица примет вид

.

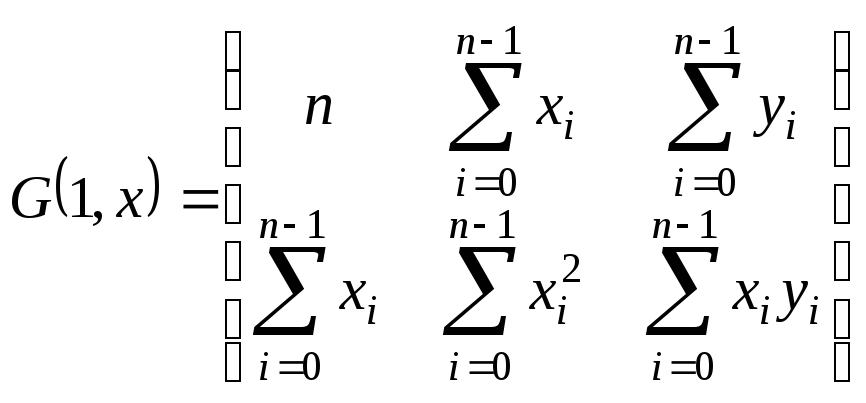Преобразуя матрицу к диагональному виду, получим следующие параметры линейной аппроксимации:

; .

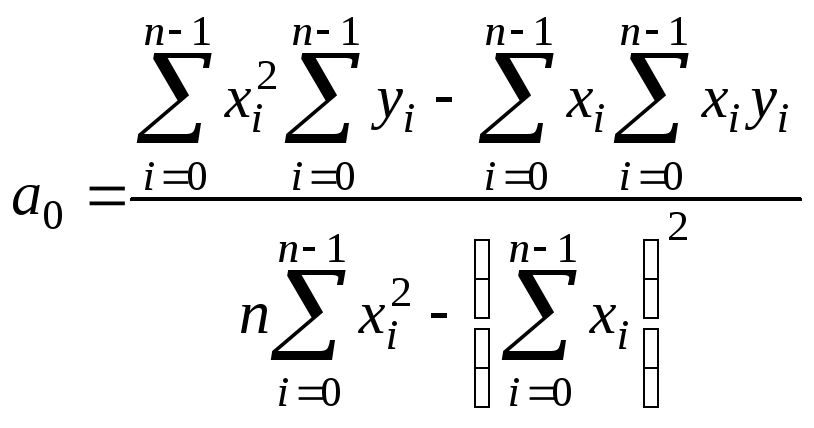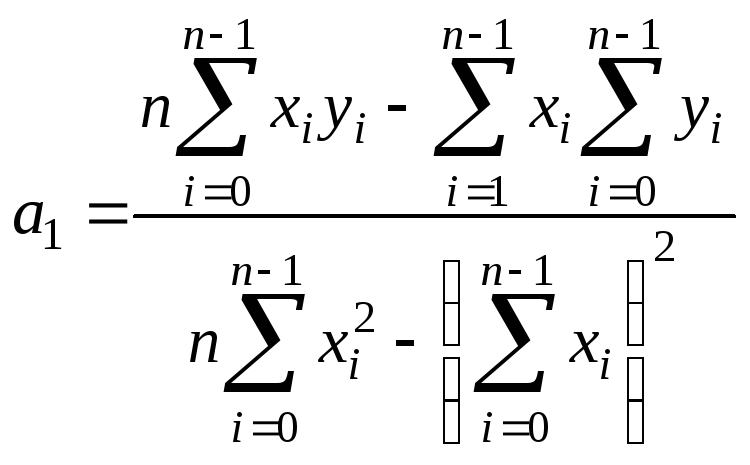Аналогично для параболической аппроксимации

расширенную матрицу можно записать в виде

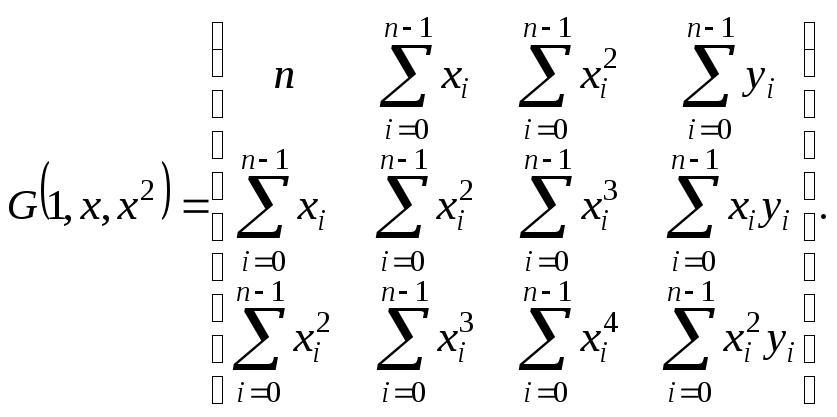
Вычисляя из экспериментальных данных необходимые суммы и диагонализируя расширенную матрицу, находим параметры аппроксимации .

Коэффициенты вычислены путем математичес-кой обработки величин, полученных с погрешностью. Поэтому аппроксимирующая функция также будет получена с погрешностью.

Подставив найденные коэффициенты в соотношение (3.1), найдем значение суммы– квадратов отклонений табличных значенийотносительно полученной аппроксимирующей функции.

Степень аппроксимирующего полинома выбирают так, чтобы обеспечить по возможности точное приближение аппроксимируемой и аппроксимирующей функций на всем интервале. При обработке экспериментальных данных, определенных с погрешностью, когда аналитическое выражение для неизвестно, обычно начинают с аппроксимации полиномом степени . После определения коэффициентов вычисляют величину . Если получится, что, то необходимо увеличить степень полинома на единицу и повторить вычисления. Увеличение и повторные вычисления необходимо осуществлять до тех пор, пока не выполнится условие .

Для контроля целесообразно на одном чертеже построить исходные точки и график аппроксимирующего полинома. При правильном выборе значения график полинома усредняет, сглаживает случайные погрешности , на всем интервале .

Многие нелинейные задачи аппроксимации могут быть сведены к линейным путем замены переменных и значений функции. При этом данные таблицы пересчитывают и представляют в виде удобном для линейной аппроксимации. Рассмотрим несколько примеров.

2. Степенная аппроксимация. Аппроксимирующая функция представляет собой нелинейную функцию параметров и

В этом случае, логарифмируя аппроксимирующую функцию, задачу можно свести к линейной аппроксимации

Покажем, как получить для степенной функции формулы из табл. 3.1.

Сумма квадратов отклонений имеет вид:

.

Частные производные по основаниям и:

,

.

Приравняв частные производные нулю, имеем

.

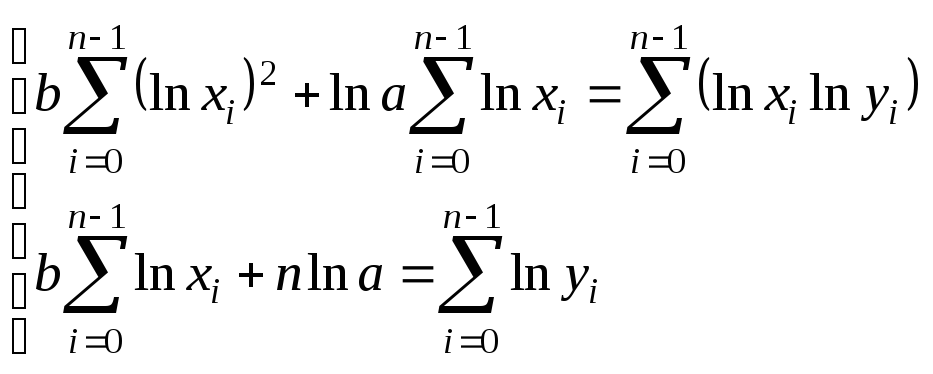Можно поступить другим способом. Введем замену переменных , а также новый параметр. Тогда

.

Таким образом, задача сведена к линейной. Для практической реализации решения задачи аппроксимации необходимо:

- прологарифмировать данные исходной таблицы;

- по новой таблице, решая линейную задачу аппроксимации, найти параметры ;

- вычислить .

3. Экспоненциальная аппроксимация .

Прологарифмируем исходную функцию . Тогда

.

Обозначим: . В результате получим

.

Задача сведена к линейной. Практически для решения данной задачи аппроксимации необходимо выполнить следующие шаги:

- прологарифмировать значения функции исходной таблицы;

- по новой таблице найти параметры ;

- вычислить .

Покажем, как получить для данной функции формулы из табл. 3.1.

Сумма квадратов отклонений имеет вид

.

Частные производные по основаниям и:

,

.

Приравняв частные производные нулю, имеем

.

В результате решения нормальной системы можно найти и, а по таблице антилогарифмов найти.

4. Гиперболическая аппроксимация .

Введем новую функцию . Задача сведена к линейной. Фактически необходимо построить новую таблицу, в которой значения аргумента остаются неизменными, а значения функции заменены обратными к начальным и, используя новую таблицу, найти параметры .

5. Гиперболическая аппроксимация .

Рассмотрим обратную функцию

Введем замену переменных . Тогда

.

Таким образом, для сведения данной нелинейной задачи к линейной достаточно заменить данные исходной таблицы обратными величинами.

6. Гиперболическая аппроксимация .

Сумма квадратов отклонений имеет вид

.

Частные производные по иравны

,

.

Приравнивая к нулю, имеем

.

Если нелинейную зависимость аппроксимирующей функ-ции от параметров нельзя представить в виде суммы (3.4), то задачу минимизации решают, используя численные итерационные методы (градиентный спуск, методы Ньютона и др.)

В табл. 3.1 приведены системы нормальных уравнений для некоторых исходных функций.

Таблица 3.1. Системы нормальных уравнений

Исходное уравнение	Система нормальных уравнений

Окончание табл. 3.1.