17.Формула ньютона для сил внутреннего трения. Коэффициент вязкости.

При течении реальной жидкости (или газов) отдельные слои воздействуют друг на друга с силами, касательными к слоям. Это явление называется внутренним трением, иливязкостью.

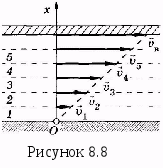
Рассмотрим течение вязкой жидкости между двумя твёрдыми пластинками, из которых нижняя неподвижна, а верхняя движется со скоростью υ_В. Условно представим жидкость в виде нескольких слоёв 1, 2, 3 и т.д. Слой «прилипший» ко дну, неподвижен. По мере удаления от дна ( нижняя пластинка) слои жидкости имеют всё большие скорости (υ₁< υ₂<υ₃<...и т.д) у слоя, который «прилип» к верхней пластинке, будет максимальная скорость υ_В.

Слои воздействуют друг на друга. Так, например, слой 3 стремится ускорить движение слоя 2, но сам испытывает торможение с его стороны, и ускоряется слоем 4 и т. д. Сила внутреннего трения пропорциональна площади S взаимодействующих слоев и тем больше, чем больше их относительная скорость. Так как разделение на слои условно, то силу принято выражать в зависимости от изменения скорости, отнесенного к длине в направлении, перпендикулярном скорости, т. е. от

Это уравнение Ньютона. Здесь η — коэффициент пропорциональности, называемый коэффициентом внутреннего трения, или динамической вязкостью (или просто вязкостью). Вязкость зависит от состояния и молекулярных свойств жидкости (или газа).

Единицей вязкости является паскаль-секунда (Па • с). Иногда вязкость выражают в пуазах¹(П):

1 Па-с = 10 п.

Жидкости, не подчиняющиеся уравнению (8.9), относят к неньютоновским. Иногда вязкость ньютоновских жидкостей называют нормальной, а неньютоновских — аномальной.

Жидкости, состоящие из сложных и крупных молекул, например растворы полимеров, и образующие благодаря сцеплению молекул или частиц пространственные структуры, являются неньютоновскими. Кровь, также является неньютоновской жидкостью.

18. Колебания

процесс, характеризующийся повторяемостью во времени и в пространстве, описывается периодической функцией:

f(t)=f(t+T_o)

Характерный признак– наличие в системе «гармонической или пропорциональной » силы направленной всегда к положению равновесия и пропорциональной смещению от положения равновесия и возвращающей осциллятор в положение равновесия

Гармонические - колебания происходящие по закону синуса или косинуса

Примеры осцилляторов: пружинный, математический и физический маятники

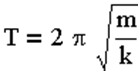
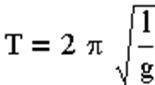
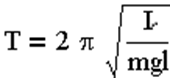
Дифференциальное уравнение гармонических колебаний и его решение.

Пусть в колебательной системе (осцилляторе) действует только гармоническая сила

F=ma,

a= dx²/dt²- ускорение материальной точки;

Разделив обе части последнего уравнения на , обозначив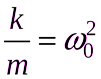

Получим

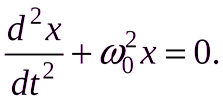
однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.

Его решением является выражение вида:

где x - смещение;

x₀- амплитуда;

w₀- собственная (круговая или циклическая) частота;

- начальная фаза.

фаза

19. 20.21

1. Свободные затухающие и вынужденные механические колебания.

Во всякой реальной системе, совершающей механические колебания, всегда действуют те или иные силы сопротивления (трение в точке подвеса, сопротивление окружающей среды и т.п.), на преодоление которых система затрачивает энергию, вследствие чего реальные свободные механические колебания всегда являются затухающими.

Затухающие колебания - это колебания, амплитуда которых убывает со временем.

Найдем закон изменения амплитуды.

Для пружинного маятника массой m, совершающего малые колебания под действием упругой силы сила трения пропорциональна скорости:

где r- коэффициент сопротивления среды; знак минус означает, чтовсегда направлена противоположно скорости.

Согласно II закону Ньютона уравнение движения маятника имеет вид:

Обозначим:

дифференциальное уравнение свободных затухающих колебаний.

Решением этого уравнения является выражение:

гдециклическая частота свободных затухающих колебаний

w₀- циклическая частота свободных незатухающих колебаний,

b - коэффициент затухания,

A₀- амплитуда в начальный момент времени (t=0).

- закон убывания амплитуды.

С течением времени амплитуда убывает по экспоненциальному закону (рис. 3).

Время релаксации - это время, за которое амплитуда уменьшается враз.

.

Таким образом, есть величина, обратная времени релаксации.

Важнейшей характеристикой затухающих колебаний является логарифмический декремент затухания .

Логарифмическим декрементом затухания называется натуральный логарифм отношения двух амплитуд, отличающихся друг от друга по времени на период:

Выясним его физический смысл.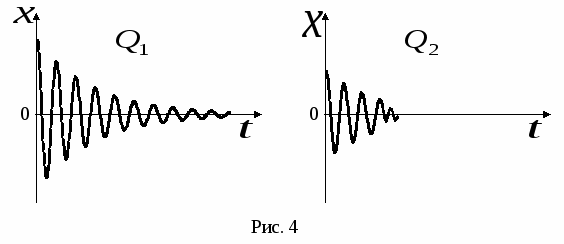

За время релаксации система успеет совершить N колебаний:

,

т.е. - это величина, обратная числу колебаний, в течение которых амплитуда уменьшается в е раз.

Для характеристики колебательной системы используют понятие добротности:

.

Добротность- физическая величина, пропорциональная числу колебаний, в течение которых амплитуда уменьшается в е раз (рис. 4,).

Вынужденными называются колебания, которые совершаются в системе под действием периодически изменяющейся внешней силы.

Пусть внешняя сила изменяется по гармоническому закону:

.

Кроме внешней силы на колеблющуюся систему действуют возвращающая сила и сила сопротивления, пропорциональная скорости колебаний:

Вынужденные колебания совершаются с частотой, равной частоте вынуждающей силы. Экспериментально установлено, что смещение отстает в своем изменении от вынуждающей силы. Можно доказать, что

где - амплитуда вынужденных колебаний,

- разность фаз колебаний и,