9. Закон сохранения импульса как фундаментальный закон природы.

Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.

(на самом деле этот закон является фундаментальным законом природы, вытекающий из определенных свойств пространства и времени. Этот закон справедлив, в отличие от закона Ньютона в любых системах отсчета, а не только в инерциальных и при любых взаимодействиях между телами. Единственное ограничение выполнение которого необходимо для справедливости З.С.И. это ЗАМКНУТОСТЬ СИСТЕМЫ. И даже это ограничение может быть нарушено, необходимо либо восстановить замкнутость, либо рассмотреть не выполняется ли условие замкнутости для некоторого выделенного направления.

В первом случае замкнутость системы восстанавливается путем включения в нее тех внешних тел, взаимодействие с которыми нарушало замкнутость.

Во втором случае необходимо найти такое направление вдоль которого выполняется условие замкнутости в том смысле, что равнодействующая всех сил действующих на эту систему, дает проекцию равно нулю на это направление.

В этом случае будет сохраняться не импульс системы, а только его проекция на данное направление.

В результате отдачи орудие приобретает некоторую скорость.)

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю.

10. Центр масс системы. Вычисление скорости центра масс.

Пусть 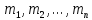— массы материальных точек, входящих в систему. Сумма масс

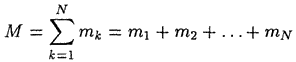
называется массой системы, а геометрическая точка С с радиусом-вектором

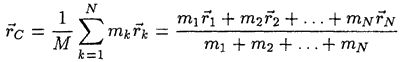
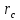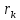
— центром масс системы. Здесь ,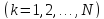радиусы-векторы центра масси материальных точек системы, проведенные из некоторого общего начала отсчета О.

Пусть система находится в однородном поле силы тяжести. Тогда, умножая числитель и знаменатель последней формулы на ускорение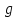силы тяжести, получим:

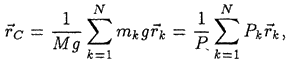
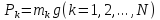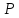где — силы веса материальных точек системы,— вес всей системы.

Мы пришли к формуле, по которой в статике определяется положение центра тяжести. Отсюда следует вывод: если механическая системанаходится в однородном поле силы тяжести, то существует понятие центра тяжести, и центр масссовпадает с центром тяжести системы. Поэтому все способы определения положения центра тяжести, ранее рассмотренные в статике, могут применяться при определении положения центра масс.

Для координат центра массв некоторой системе координатных осей Oxyz, проектируя на эти оси векторную формулу для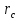, получаем:

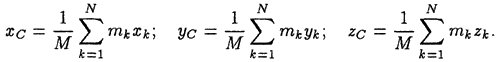
Здесь 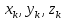— координаты материальных точек системы.

Масса М и радиус-вектор центра масс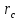с являются важными характеристиками инертных свойств системы, но полностью эти свойства не определяют. Для полной характеристики инертных свойств системы требуется указать еще моменты инерциисистемы.

Скорость центра масс

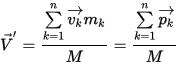(М— масса всей системы тел), (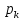— импульсы частиц)2.

12. Работа и кинетическая энергия. Мощность.

Энергия — универсальная мера различных форм движения и взаимодействия.

Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.

Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол а с направлением перемещения, то работа этой силы равна произведению проекции силы Fs на направление перемещения (Fs = Fcos а), умноженной на перемещение точки приложения силы:

Сила может изменяться как по модулю, так и по направлению, поэтому в общем случае формулой (11.1) пользоваться нельзя. Если, однако, рассмотреть элементарное перемещение dr, то силу F можно считать постоянной, а движение точки ее приложения — прямолинейным.

Элементарной работой силы F на перемещении dr называется скалярная величина

где а — угол между векторами F и dr;

ds = |dr| — элементарный путь;

Fs — проекция вектора F на вектор df (рис. 13).

Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути:

Для вычисления этого интеграла надо знать зависимость силы Fs от пути s вдоль траектории 1 — 2. Пусть эта зависимость представлена графически:

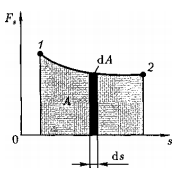
Тогда искомая работа А определяется на графике площадью затонированной фигуры. Если, например, тело движется прямолинейно, сила F= const и а = const, то получим:

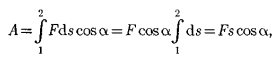
где s — путь, пройденный телом.

Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой 1 Н на пути 1 м (1 Дж = 1 Н • м).

Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:

За время dt сила F совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент времени: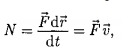т.е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная.

Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = = 1 Дж/с).

Кинетическая энергия механической системы — энергия механического движения этой системы.

Тело массой т, движущееся со скоростью v, обладает кинетической энергией:

В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а, следовательно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетическая энергия зависит от выбора системы отсчета.

Кинетическая энергия механической системы равна сумме кинетических энергий тел, входящих в систему. Так, кинетическая энергия системы из n материальных точек равна:, где Vi — скорость i-й материальной точки массой mi.

11.

Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки 0 данной оси. Значение момента импульса L_z не зависит от положения точки 0 на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси каждая отдельная точка тела движется по окружности постоянного радиуса r_i с некоторой скоростью v_i. Скорость v_i и импульс m_iv_i перпендикулярны этому радиусу, т.е. радиус является плечом вектора m_iv_i. Поэтому можно записать, что момент импульса отдельной точки относительно оси z равен

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных его точек:

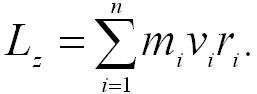
Учитывая связь между линейной и угловой скоростями (v_i = ωr_i), получим следующее выражение для момента импульса тела относительно неподвижной оси:

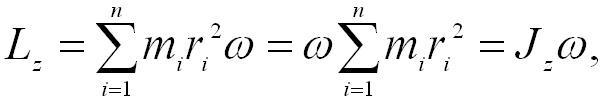(4.12)

т.е. момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.

Продифференцировав выражение (4.12) по времени, получим:

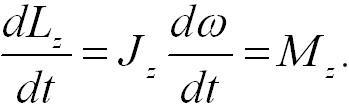(4.13)

Это еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: скорость изменения момента импульса тела относительно неподвижной оси вращения равна результирующему моменту относительно этой оси всех внешних сил, действующих на тело.

Закон сохранения момента импульса вытекает из основного уравнения динамики вращательного движения тела, закрепленного в неподвижной точке (уравнение 4.8), и состоит в следующем:

если результирующий момент внешних сил относительно неподвижной точки тождественно равен нулю, то момент импульса тела относительно этой точки с течением времени не изменяется.

Действительно, если M = 0, то dL / dt = 0 , откуда

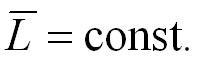(4.14)

Другими словами, момент импульса замкнутой системы с течением времени не изменяется.

Из основного закона динамики тела, вращающегося вокруг неподвижной оси z (уравнение 4.13), следует закон сохранения момента импульса тела относительно оси:

если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется в процессе движения, т.е. если M_z = 0, то dL_z / dt = 0, откуда

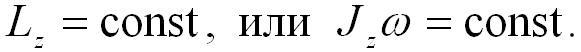(4.15)

Закон сохранения момента импульса является фундаментальным законом природы. Справедливость этого закона обусловливается свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета.

Справедливость закона сохранения момента импульса относительно неподвижной оси вращения можно продемонстрировать на опыте со скамьей Жуковского. Скамьей Жуковского называется горизонтальная площадка, свободно вращающаяся без трения вокруг неподвижной вертикальной оси ОО₁. Человек, стоящий или сидящий на скамье, держит в вытянутых руках гимнастические гантели и приводится во вращение вместе со скамьей вокруг оси ОО₁ с угловой скоростью ω₁. Приближая гантели к себе, человек уменьшает момент инерции системы, а так как момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость ее вращения ω₂ возрастает. Тогда по закону сохранения момента импульса относительно оси ОО₁ можно записать:

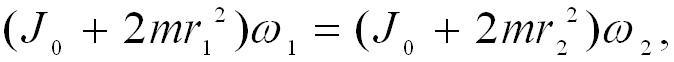(4.16)

где J₀ - момент инерции человека и скамьи; 2mr₁² и 2mr₂² - моменты инерции гантелей в первом и втором положениях; m – масса одной гантели; r₁, r₂ – расстояния от гантелей до оси ОО₁.

Изменение момента инерции системы связано с изменением ее кинетической энергии:

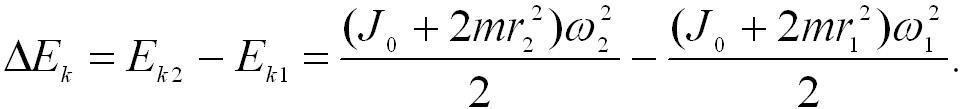
Используя выражение для ω₂, полученное из (4.16)

после преобразований получим:

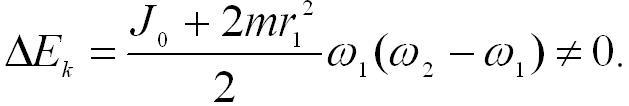
Это изменение кинетической энергии системы численно равно работе, совершенной человеком при перемещении гантелей.

В табл. 4.2 сопоставлены основные физические величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение.

Таблица 4.2

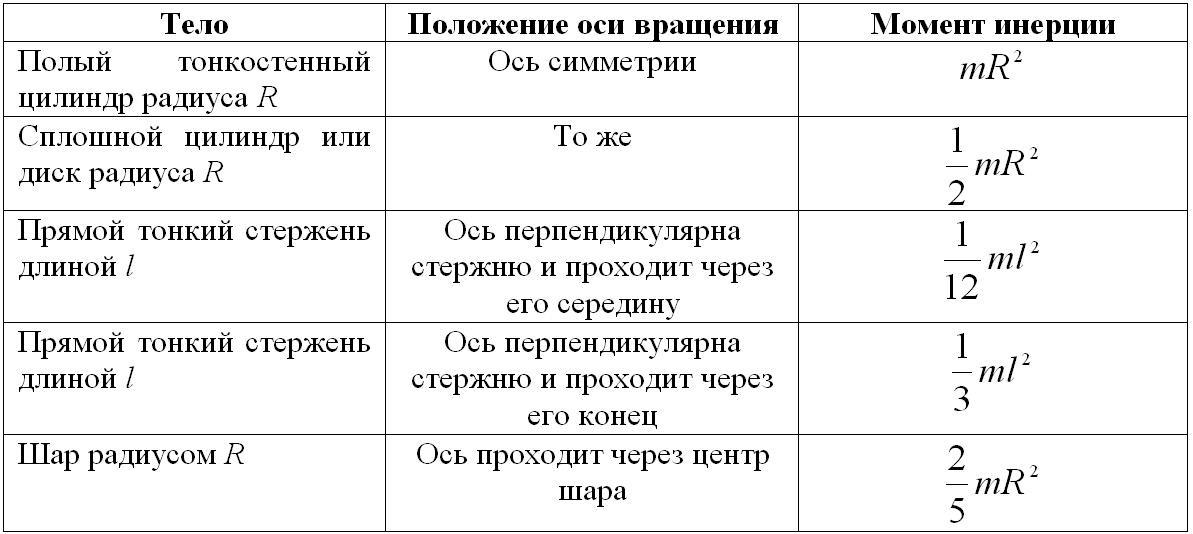
Краткие выводы

• Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

• Момент инерции тела относительно оси вращения – это физическая величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний до рассматриваемой оси:

• 

• Момент инерции тела J_z относительно любой оси вращения равен моменту его инерции J_c относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:

• 

• При вращении абсолютно твердого тела вокруг неподвижной оси z его кинетическая энергия равна половине произведения момента инерции относительно оси вращения на квадрат угловой скорости:

• 

• Из сравнения формул 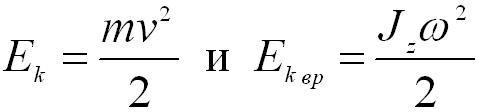следует, чтомомент инерции – мера инертности тела при вращательном движении.

• Работа вращения тела идет на увеличение его кинетической энергии и определяется выражением dA = M_zdφ, где M_z – момент сил относительно оси вращения z.

• Уравнение динамики вращательного движения твердого тела относительно неподвижной оси z (аналог второго закона Ньютона) имеет вид:

• 

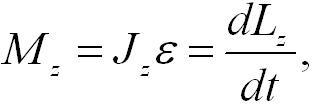
• где L_z – момент импульса твердого тела относительно оси z.

• В замкнутой механической системе момент внешних сил относительно неподвижной оси M_z = 0 и dL_z / dt = 0, откуда L_z = const – закон сохранения момента импульса. Он является следствием изотропности пространства: инвариантность физических законов относительно выбора направления осей координат системы отсчета.