13. Закон сохранения полной механической энергии.

Закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем:

Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние), называются консервативными системами.

Закон сохранения механической энергии можно сформулировать так: в консервативных системах полная механическая энергия сохраняется.

Закон сохранения механической энергии связан с однородностью времени. Однородность времени проявляется в том, что физические законы инвариантны относительно выбора начала отсчета времени.

Существует еще один вид систем — диссипативные системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс получил название диссипации (или рассеяния) энергии.

В консервативных системах полная механическая энергия остается постоянной. Могут происходить лишь превращения кинетической энергии в потенциальную и обратно в эквивалентных количествах так, что полная энергия остается неизменной.

Этот закон не есть просто закон количественного сохранения энергии, а закон сохранения и превращения энергии, выражающий и качественную сторону взаимного превращения различных форм движения друг в друга.

Закон сохранения и превращения энергии — фундаментальный закон природы, он справедлив как для систем макроскопических тел, так и для систем микротел.

В системе, в которой действуют также неконсервативные силы, например, силы трения, полная механическая энергия системы не сохраняется. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида.

14. Момент инерции твердого тела. Момент импульса. Теорема Штейнера.

Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстоянии до рассматриваемой оси:

Суммирование производится по всем элементарным массам m, на которые разбивается тело.

В случае непрерывного распределения масс эта сумма сводится к интегралу: где интегрирование производится по всему объему тела.

Величина r в этом случае есть функция положения точки с координатами х, у, z. Момент инерции — величина аддитивная: момент инерции тела относительно некоторой оси равен сумме моментов инерции частей тела относительно той же оси.

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера:

момент инерции тела J относительно произвольной оси равен моменту его инерции Jс относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы тела на квадрат расстояния а между осями:

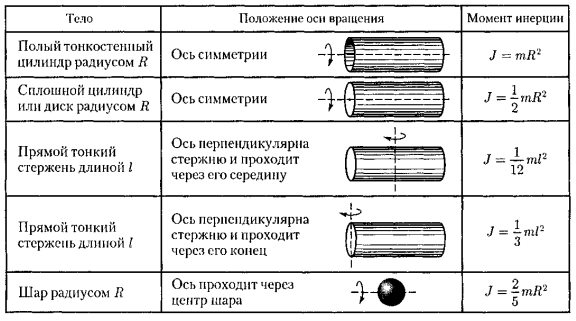
Примеры моментов инерции некоторых тел (тела считаются однородными, m — масса тела):

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

где r — радиус-вектор, проведенный из точки О в точку А;

р = mv — импульс материальной точки;

L — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

Модуль вектора момента импульса:

где а — угол между векторами r и р;

l — плечо вектора р относительно точки О.

Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса r, с некоторой скоростью Vi. Скорость Vi и импульс mV перпендикулярны этому радиусу, т. е. радиус является плечом вектора . Поэтому момент импульса отдельной частицы равен:

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

Используя формулу получим, что момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость: