42. Условия возникновения дифракционного максимума и минимума.

Если число зон Френеля четное, то

(m= 1, 2, 3, …), наблюдается дифракционный минимум(колебания от каждой пары соседних зон взаимно гасят друг друга)

Если число зон Френеля нечетное, то

(m= 1, 2, 3, …), наблюдается дифракционный максимум(одна зона Френеля не скомпенсирована).

В направлении =0 щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью т.е. наблюдаетсяцентральный дифракционный максимум.

Из условий максимума и минимума направления на точки экрана, где амплитуда (и интенсивность ) максимальна -и минимума -

43. Дифракция Фраунгофера и спектральное разложение. Разрешающая способность и дисперсия дифракционной решетки.

Назначение спектральных приборов – исследовать спектральный состав излучения, т.е. определять, из каких монохроматических волн оно состоит.

Дифракционная решетка является спектральным прибором, поскольку положение главных максимумов зависит от длины волны . При пропускании через решетку белого света все главные максимумы, кроме нулевого, раскладываются в спектры так, что внутренним краем являются фиолетовые, а наружным – красные лучи. Спектры первого, второго и так далее порядков располагаются симметрично по обе стороны от нулевого. Расстояния между соответствующими линиями спектров возрастают по мере увеличения порядка спектра. Спектры высших порядков могут перекрываться.

Основными характеристиками любого спектрального прибора являются угловая и линейная дисперсия, разрешающая способность (сила) .

1. Угловой дисперсией называется величина

,

- угловое расстояние между спектральными линиями, отличающимися по длине волны на .

Можно сказать, что угловая дисперсия определяет угловое расстояние между линиями, отличающимися по длине волны на 1А^o.

Дифференцируя условие максимумов для дифракционной решетки -

,

при данном m, находим формулу угловой дисперсии для решетки,

.

Из этой формулы видно, что для заданного порядка m спектра угловая дисперсия тем больше, чем меньше период d решетки. Кроме того, величина угловой дисперсии растет с увеличением порядка спектра m.

2. Линейной дисперсией называют величину

,

где - линейное расстояние на экране или на фотопластинке между спектральными линиями, отличающимися по длине волны на.

Можно сказать, что линейная дисперсия D_лин – это линейное расстояние между линиями на экране, отличающимися по длине волны на 1А^o.

,

где F– фокусное расстояние линзы, проектирующей спектр на экран.

3. Разрешающей способностью (разрешающей силой) спектрального прибора называют безразмерную величину

,

где – абсолютное значение минимальной разности длин волн (,) двух близких спектральных линий, при которой эти линии регистрируются раздельно (то есть разрешаются прибором).

Два близких максимума воспринимаются глазом раздельно (небольшой провал посредине воспринимается глазом по контрасту как наличие тёмного промежутка между максимумами для и) в том случае, если интенсивность в промежутке между ними составляет не более 80% от интенсивности максимума. Согласно критерию, предложенному Рэлеем, такое соотношение интенсивностей имеет место в том случае, если середина одного максимума совпадает с краем другого. Т.е. спектральные линии с разными длинами волн, но одинаковой интенсивности, считаются разрешенными, если главный максимум одной спектральной линии совпадает с первым минимумом другой, как это показано на рис. 6.

Рис 6

В этом случае между двумя максимумами возникает провал, составляющий около 20% от интенсивности в максимумах, и линии еще воспринимаются раздельно.

Таким образом, необходимо, чтобы максимум m-ого порядка линии с длиной волны (рис. 6) совпадал по направлению с первым минимумом линии , то есть

,

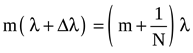Отсюда следует, что разрешающая способность дифракционной решетки может быть определена по формуле

.

Наибольший порядок спектра, который можно получить с данной решеткой, ограничивается условием .