Затухающие электромагнитные колебания

Они происходят в колебательном контуре, содержащим активное сопротивление R

Сумма падений напряжения на емкости и активном сопротивлении = ЭДС самоиндукции на сопротивление

Или гдеq– заряд обкладки конденсатора

Или

Подставим в уравнение

Введем обозначения ,тогда получим дифференциальное уравнение свободных затухающих электромагнитных колебаний

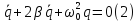
Решением этого уравнения будет

– это меняющаяся со временем амплитуда затухающих колебаний

Найдем силу тока в колебательном контуре I:, где γ – угол, удовлетворяющий условию π>γ>π/2

Логарифмический декремент затухания

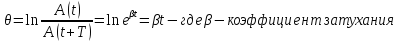
t_e – время релаксации в течении которого амплитуда убывает вераз (е=2.71)

Тогда можно записать

Откуда получим

Тогда число колебаний, в течение которых амплитуда убывает в eраз

Добротность

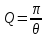
Для механических колебаний а при слабом затухании

Тогда добротность

Для колебательного контура при слабом затухании 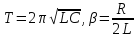и добротностьQможно найти по формулам:(10)

Из формул 7 и 8 получим: , т.е. (смысл) добротность в π раз больше числа колебаний в течении которых амплитуда убывает в е раз

Мощность потерь механической системы

При малом затухании (β<<ω₀) можно пренебречь изменениями мощностиPпо сравнению с энергией колебательной системыW

Тогда получим, что Wубывает со временем по закону:, где β-коэф. затуханияW-энергия приt=0

Как для электромагнитных, так и механических

Вынужденные электромагнитные колебания

Рассмотрим колебательный контур, содержащий емкость C, индуктивностьюL, сопротивлениеRи вынуждающую ЭДС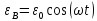или переменное напряжение

Cумма падения напряжения на конденсаторе и активном сопротивлении = сумме ЭДС самоиндукции и вынуждающему переменному напряжению

Подставим в это , поделим результат на индуктивность, введем обозначения:

Тогда получим дифференциальное уравнение вынужденных электромагнитных колебаний:

Его решение имеет вид , где амплитуда зарядаqmна обкладках конденсатора и сдвиг фазы γ определяются по формулах:

Резонансная частота заряда qопределяется по формуле:

Дифференцирую формулу 3 по времени, найдем силу тока в колебательном контуре:

Где с учётом формулы (4) амплитуда сила тока

Введем угол , тогда

А вместо формулы (6) вместо тока получим

Амплитуда силы тока I_mявляется функцией частоты колебаний ω

На рисунке – графики зависимости амплитуды силы тока для разных сопротивлений

Из формулы 7 видно, что амплитуда силы тока максимальна при частоте, удовлетворяющей условию

Отсюда получим

, где ω₀– собственная частота колебательного контура.

Оценим ширину резонансного пика

Чем больше добротность Q, тем меньше ширина резонансного пика.

Колебания в колебательном контуре можно рассмотреть, как переменный ток в цепи из последовательно как переменный ток в цепи из последовательно соединенных сопротивления R, индуктивностиLи емкостиC

К такой цепи подключено переменное напряжение 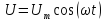, а в цепи протекает ток

Формулу 7 можно рассматривать как запись закона Ома для амплитуд Imи напряженностиUm, величинаЭто называется полным электрическим сопротивлением цепи.

Рассмотрим частные случаи с помощью этой формулы и формулы 8:

1. В отсутствие индуктивности (L= 0) и конденсатора (C=∞), ϕ=0,Z=R. В цепи протекает ток

2. В отсутствие сопротивления (R=0) и конденсатора (С=∞), ϕ=π/2,z=ω Сила тока-реактивное индуктивное сопротивление цепи Напряжение опережает по фазе силу тока на

3. В отсутствие сопротивления (R=0) и индуктивности (L=0), ϕ=-π/2,Z=1/ωCCила токагдеZc– емкостное реактивное индуктивное сопротивление цепи Напряжение отстает по фазе от силы тока на π/2.