
- •Предисловие
- •Общие рекомендации студенту заочнику
- •Работа с учебником
- •Решение типовых задач
- •Ответы на тестовые задания
- •Установочные лекции и практические занятия
- •Контрольные вопросы
- •Зачеты и экзамены
- •Требования к выполнению контрольных работ
- •1. Неопределенный интеграл
- •1.1. Основные понятия и свойства
- •1.2. Способы нахождения интегралов
- •1.2.1. Табличное интегрирование
- •1.2.2. Линейное преобразование выражения под знаком дифференциала
- •1.2.3. Подведение (внесение) под знак дифференциала
- •1.2.4. Замена переменной в неопределенном интеграле
- •1.2.5. Интегрирование по частям
- •1.3. Интегрирование рациональных выражений
- •1.4. Интегрирование иррациональных выражений
- •1.5. Интегрирование тригонометрических выражений
- •2. Определенный интеграл
- •2.1. Основные свойства и определения
- •2.2. Замена переменной в определенном интеграле
- •2.3. интегрирование по частям в определенном интеграле
- •2.4. Несобственные Интегралы
- •2.4.1. Несобственные интегралы с бесконечными пределами (I рода)
- •2.4.2. Несобственный интегралы от неограниченных функций (II рода)

|
|
|
|
sect |
= |
x |
; |
tgt = |
|
x2 − |
4 |
|
|
|
|
|
|
|
|
|
||||
Так как |
2 |
|
2 |
|
. |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
|
x2 |
− 4 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
cost |
= |
; |
sin t |
= |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Следовательно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
I = |
2 |
sin t |
+ |
1 |
ln sect + tgt + C = 2 |
x2 |
− 4 x2 |
+ |
1 |
ln |
x |
+ |
x2 − 4 |
+ C = |
||||||||||
cos2 t |
2 |
|
4x |
2 |
2 |
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||
|
x x2 |
− 4 |
|
1 |
|
x + x2 − 4 |
|
|
|
|
|
|
|
|
|
|
||||||||
= |
+ |
ln |
+ C |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
x x2 − 4 |
+ |
1 |
ln |
x + x2 |
− 4 |
+ C . |
|
|
|
|
|
|
|
||||||||||
|
2 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.5. Интегрирование тригонометрических выражений
Интегралы от тригонометрических выражений различного типа во многих ситуациях удается рационализировать либо существенно упростить.
Типы тригонометрических выражений и способы их интегрирования
1. Универсальная тригонометрическая подстановка t = tg |
u |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
|
|
|
|
= t; x = 2arctg t; dx = |
|
|
|
|
|
|
|
|
|
|
|
2t |
|
1− t 2 |
2dt |
||||||||||||||||||||||||||||||||
∫ R(sin x, cos x)dx = |
|
2 |
|
(1+ t 2 ) |
|
= |
∫ R( |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1− t 2 |
|
|
|
|
|
|
|
|
|
2t |
|
|
|
|
|
|
|
|
|
|
;1+ t2 ) |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
cos x |
= |
; sin x = |
|
|
|
|
|
1+ t 2 |
|
1+ t 2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ t 2 |
1+ t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пример 32. Найти интеграл ∫ |
|
|
|
|
dx |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
sin3 3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
dx |
|
|
tg |
x |
= t; x = 2arctg t; dx = |
|
|
2dt |
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
1 |
(1+ t 2 ) |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
1+ t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
∫ |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2t |
|
|
|
= 2∫ |
|
|
|
|
|
|
|
= |
4 ∫ |
|
|
|
|
dt |
||||||||||||||||||||||||||||
sin3 3x |
|
|
|
|
|
sin x = |
|
|
|
(1+ t 2 )( |
2t |
)3 |
|
|
t3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
+ t2 |
|
|
|
|
|
|
1+ t 2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
1 |
1 2 |
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
2 x |
|
|
1 |
|
|
|
x |
|
|
|
|
2 x |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
= 4 |
∫( |
|
|
+ t |
+ t)dt = − |
|
|
|
+ 2 ln |
|
t |
|
+ t |
|
|
+ C |
= − |
8 ctg |
|
|
|
+ |
2 ln |
tg |
|
|
|
+ tg |
|
|
+ C |
|
||||||||||||||||||||||||||||||||||
t3 |
8t2 |
|
|
2 |
|
2 |
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Ответ: − |
1 |
ctg |
2 |
x |
+ |
|
1 |
ln |
|
tg |
x |
|
+ tg 2 |
x |
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
8 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
dx
Пример 33. Найти интеграл∫ 5 + 2sin x + 3cos x .
Решение
= ∫ R* (t)dt (1.5.1)
=
27
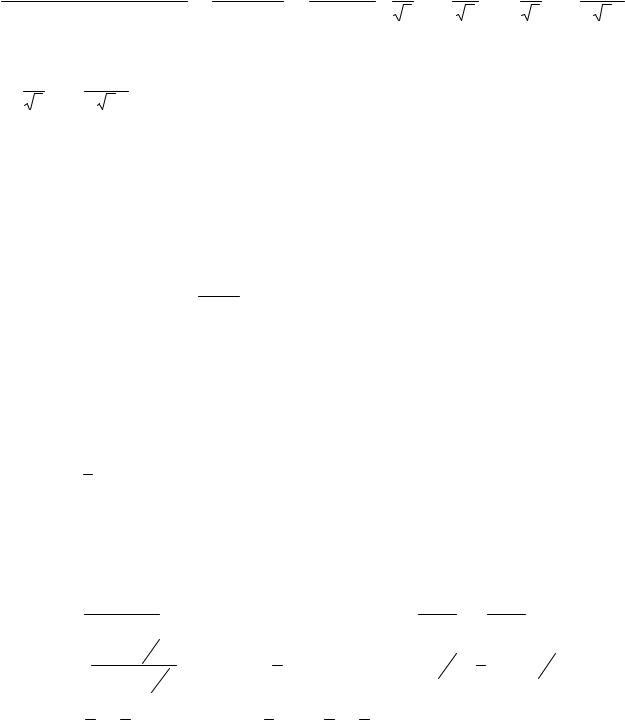
|
|
|
|
dx |
|
|
|
|
|
tg |
x |
= t; x |
= 2arctg t; dx |
= |
|
2dt |
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
(1+ t 2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
∫ |
|
|
|
|
|
= |
|
2 |
|
|
|
− t 2 |
|
|
= ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
||||||||||
5 + 2sin x + 3cos x |
|
|
|
|
|
1 |
|
|
2t |
|
|
|
|
2 |
|
|
|
|
4t |
|
|
3 − 3t 2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos x = |
|
|
2 ; sin x = |
|
|
|
|
|
|
|
(1+ t |
|
) 5 |
+ |
|
|
|
|
+ |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ t |
1+ t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ t |
2 |
1+ t |
2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
x |
+ 1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
dt |
|
|
2 |
|
|
|
|
t + 1 |
|
|
2 |
|
|
|
||||||||
∫ |
|
|
|
|
|
|
|
|
|
|
|
= ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||
|
2 |
5 + 5t 2 |
+ 4t + 3 − 3t 2 = ∫ |
2t 2 + 4t + 8 |
(t + 1)2 + 3 |
= |
3 arctg |
3 |
+ C = |
3 arctg |
|
|
3 |
+ C |
||||||||||||||||||||||||||||
|
(1+ t |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
tg |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3 arctg |
3 |
|
|
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2. Применение замены t = tgx .
|
m + n = 2 p; tgx = t; sin2 x = |
|
|
t2 |
|
|
||||||
∫ sinm x cosn x dx = |
1 |
+ t2 |
= ∫ R(t)dt |
|||||||||
|
|
|
1 |
|
||||||||
|
cos2 x = |
|
|
; x = arctg t; dx = |
|
dt |
|
|||||
1 |
+ t2 |
1 + t2 |
|
|||||||||
|
|
|
|
|
|
|||||||
dx
Пример 34. Найти интеграл ∫ cos4 x .
Решение
∫ |
dx |
= |
tg x = t; cos |
2 |
x = |
1 |
; dx = |
dt |
= ∫ |
(1+ t 2 )2 dt |
= ∫(1+ t2 )dt |
|
1+ t 2 |
1+ t 2 |
|||||||||
cos4 x |
|
1+ t2 |
|||||||||
|
|
|
|
x = arctg t |
|
|
|
|
|
||
= tg x + 13 tg3 x + C
Ответ: tg x + 13 tg3 x + C .
|
|
|
cos6 x |
|
Пример 35. Найти интеграл ∫ sin 4 x dx . |
|
|||
Решение |
|
|
|
|
cos6 x |
(1− sin 2 x)3 |
dx = ∫ |
1− 3sin2 x + 3sin 4 x − sin6 x |
dx |
∫ sin 4 x dx = ∫ |
sin 4 x |
sin 4 x |
dx = ∫ sin 4 x |
|
(1.5.2)
= t + t3 + C =
3
dx |
+ 3∫dx + |
− 3∫ sin 2 x |
− ∫sin |
2 |
x dx = ∫ |
|
d(x + π 2) |
+ 3ctg x + 3x − |
1 |
∫(1− cos 2x)dx = tg(x + |
π |
2 |
) + |
1 |
tg |
3 |
(x + π |
2 |
) + |
|||||||||||||
|
cos |
4 |
(x + |
π |
2) |
2 |
3 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 ctg3 x + |
5 x + |
1 sin 2x + C |
|
|
|
|
|
|
|
|
|
|||||||||
+ 3ctg x + 3x − |
1 x + |
1 sin 2x + C |
= −ctg x − |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
3 |
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
Ответ: − ctg x − |
1 |
ctg3 x + |
|
5 |
x + |
1 |
sin 2x + C . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. Внесение под знак дифференциала функции в нечетной степени
28

∫sin m x cosn x dx = |
sin |
|
∫ (1.5.3) |
= −∫ (1 − t2 ) p tn dt = |
|
|
, |
т.е. m - нечетное число.
Пример 36. Найти интеграл ∫cos5 x dx .
Решение
∫cos5 x dx = ∫cos4 x d(sin x) = ∫(1− sin 2 x)2 d(sin x) = ∫(1− 2sin x + sin 4 x) d(sin x) =
= sin x − |
2 sin3 |
x + |
1 sin5 |
. |
x + C |
||||
|
3 |
|
5 |
|
Ответ: sin x − 23 sin3 x + 15 sin5 x + C .
Пример 37. Найти интеграл ∫ sindxx .
Решение
∫ |
dx |
= ∫ |
sin x dx |
= −∫ |
d(cos x) |
= |
1 |
|
1 − cos x |
|
+ С |
|
|
|
|||||||||||
|
sin2 x |
|
2 ln |
|
|
|
|
|||||
sin x |
1 − cos2 x |
|
|
1 + cos x |
||||||||
Ответ: 12 ln 11 +− coscos xx + С .
4). Понижение порядка выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m + n = 2 p; m ≥ 0; n ≥ 0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
∫sin m x cosn x dx = |
sin 2 x = |
1 |
(1− cos 2x); cos2 x = 1 (1+ cos 2x) |
|
(1.5.4) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x cos x = |
sin 2x |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
Пример 38. Найти интеграл∫sin 2 5x cos4 5x dx . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
∫sin 2 5x cos4 5x dx = ∫ |
(sin 5x cos5x) cos2 5x dx = ∫ |
sin 2 10x |
|
|
(1+ cos10x) |
dx = |
|
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
4 |
|
|
2 |
|
|
|
|
||||
∫sin 2 10x dx + |
∫sin 2 |
10x cos10x dx = |
∫(1− cos 20x)dx + |
|
1 |
∫sin 2 |
10x d(sin10x) = |
|
||||||||||||||||||||||||
8 |
|
|
80 |
|
||||||||||||||||||||||||||||
|
1 |
|
|
1 |
|
8 |
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
= |
|
x − |
|
sin 20x + |
|
1 |
sin3 10x + C |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
16 |
320 |
240 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ответ: |
|
1 |
x − |
1 |
sin 20x + |
1 |
sin3 10x + C . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
16 |
320 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
240 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5). Случай четных степеней тригонометрических функций
29
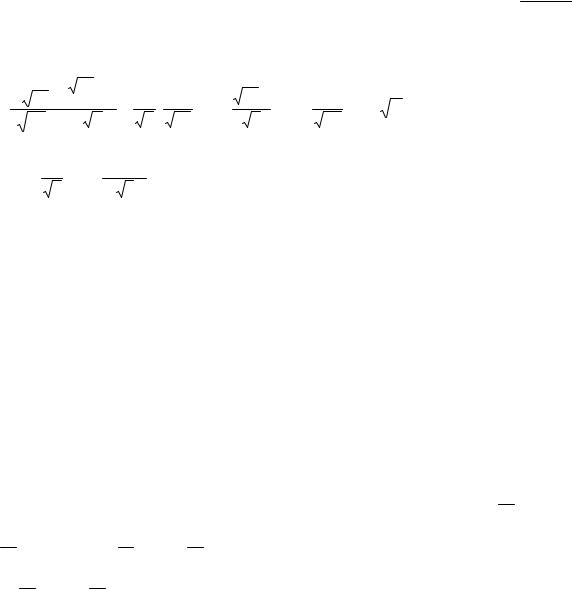
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgx = t; x = arctgt |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
∫ R(sin 2 x, cos2 x,sin x cos x)dx = |
dx = |
|
|
|
dt |
|
|
; sin 2 x = |
t 2 |
|
= |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
(1 |
2 |
) |
1+ t |
2 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ t |
|
|
1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 x = |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ t 2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
= ∫ R( |
|
t 2 |
|
; |
|
|
1 |
|
; |
|
t |
|
|
) |
2dt |
= ∫ R |
** |
(t)dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
1+ t 2 |
1+ t 2 |
1+ t 2 |
1+ t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Пример 39. Найти интеграл ∫ |
|
|
|
|
|
|
dx |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2cos2 x + 10sin 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
dx |
|
|
|
|
|
|
|
tgx = t; x = arctgt |
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
∫ |
|
|
|
|
|
= |
dx = |
|
|
dt |
|
|
; sin |
2 |
x |
= |
|
|
= ∫ |
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
= |
||||||||||||||||||
2 cos2 x + 10 sin 2 x |
|
(1 + t2 ) |
|
1 + t2 |
|
|
(1 + t |
2 |
|
|
2 |
|
+ |
10t2 |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ t |
2 |
1 + t |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
2 x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
1 |
d( |
10 t) |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
10 t |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= ∫ |
10 |
|
= |
|
arctg |
|
|
+ C = |
|
|
arctg |
|
|
2 tgx + C |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
( 10 t) |
+ ( 2) |
|
|
|
|
|
|
5 |
|
20 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(1.5.5)
dt
∫ 10t2 + 2 =
|
2 |
tg |
x |
+ 1 |
|
Ответ: |
2 |
|
|||
3 arctg |
|
|
3 |
+ C . |
6. Использование формул для преобразования произведений тригонометрических функций от различных аргументов
sin u sin v = − 1 [sin(u − v) + sin(u + v)] |
(1.5.6) |
|||
|
2 |
|
||
cos u cos v = |
1 |
[cos(u − v) + cos(u + v)] |
(1.5.7) |
|
|
2 |
|
|
|
sin u sin v = |
1 |
|
[cos(u − v) − cos(u + v)] |
(1.5.8) |
2 |
|
|||
|
|
|
|
|
Пример 40. Найти интеграл ∫cos7x cos x dx .
Решение
∫cos7x cos x dx = 12 ∫[cos(7 −1)x + cos(7 + 1)x]dx = 12 ∫cos6xdx + 12 ∫cos8xdx = 121 ∫cos6xd(6x) + + 161 ∫cos8xd(8x) = 121 sin 6x + 161 sin 8x + C
Ответ: 121 sin 6x + 161 sin 8x + C .
Пример 41. Найти интеграл∫sin 6x sin 4x dx .
30
Решение
∫sin 6x sin 4x dx = − 12 ∫[cos(6 − 4)x − cos(6 + 4)x]dx = − 12 ∫cos 2xdx + 12 ∫cos10xdx = − 14 ∫cos 2xd(2x) + 201 ∫cos10xd(10x) = − 14 sin 2x + 201 sin10x + C
Ответ: − 14 sin 2x + 201 sin10x + C .
Пример 42. Найти интеграл∫sin12x cos6x dx .
Решение
∫sin12x cos6x dx = 12 ∫[sin(12 − 6)x + sin(12 + 6)x]dx = 12 ∫sin 6xdx + 12 ∫sin18xdx = = 121 ∫sin 6xd(6x) + 361 ∫sin18xd(18x) = − 121 cos6x − 361 cos18x + C
Ответ: − 121 cos6x − 361 cos18x + C .
7). Интегралы вида ∫tg m x |
secn xdx и ∫ctg m x cosecn xdx , (где n - четное число вычисляются |
с помощью формул sec2 x = 1 |
+ tg 2 x или cosec2 x = 1+ ctg 2 x |
Пример 43. Найти интеграл∫tg 5 x dx .
Решение
∫tg |
5 |
x dx = ∫tg |
2 |
x tg |
3 |
xdx = ∫ |
1 |
|
−1)tg |
3 |
xdx = ∫tg |
3 |
x |
dx |
− ∫tg |
2 |
x tgx |
dx |
|
= |
|||||||||||||
|
|
|
( |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
cos2 x |
|
|
cos2 x |
|
cos2 |
x |
||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
1 |
4 |
|
|
|
1 |
|
|
1 |
|
4 |
|
|
|
dx |
|
|
|||||
= ∫tg |
|
xd(tgx) |
−∫tgxd(tgx) = |
4 tg |
|
x |
− ∫( |
|
−1)tgxdx = 4 tg |
|
x − ∫tgx |
|
+ ∫tgxdx = |
||||||||||||||||||||
|
|
cos2 x |
|
cos2 x |
|||||||||||||||||||||||||||||
= 1 tg 4 x − 1 tg 2 x − ln |
|
cos x |
|
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: 14 tg 4 x − 12 tg 2 x − ln cos x + C .
Пример 44. Найти интеграл∫ctg3 x dx .
Решение
∫ctg |
3 |
x dx = ∫ctg |
2 |
x ctgxdx = ∫( |
1 |
|
− 1)ctgxdx = ∫ctgx |
dx |
|
− ∫ctgxdx = − ∫ctgxd(ctgx) − |
|
|||||||||||||||||||||
|
|
|
sin |
2 |
x |
sin |
2 |
x |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
− ∫ |
cos x |
dx = − |
1 |
ctg 2 x − ∫ |
d(sin x) |
= − |
1 |
ctg 2 x − ln |
|
sin x |
|
+ C |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
sin x |
2 |
|
|
sin x |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
8). Интегралы вида ∫sec2n+1 xdx и ∫cosec2n+1 xdx вычисляются по рекуррентным формулам |
||||||||||||||||||||||||||||||||
как интегралы от нечетной положительной степени секанса и косеканса: |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
∫sec |
2n+1 |
|
|
1 |
|
sin x |
1 |
)∫sec |
2n−1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
xdx = |
|
|
+ (1 |
− |
|
|
xdx |
(1.5.10) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2n |
cos2n |
2n |
|
|||||||||||||||||||
31

∫cosec |
2n+1 |
|
1 |
cos x |
|
1 |
)∫cosec |
2n−1 |
|
|
|
xdx = − |
|
sin 2n |
+ (1− |
|
|
xdx |
(1.5.11) |
||
|
2n |
2n |
|
Пример 45. Найти интеграл∫tg 4 x sec6 xdx .
Решение
∫tg 4 x sec6 xdx = ∫tg 4 x(1+ tg 2 x)2 sec2 xdx = ∫tg 4 x(1+ tg 2 x)2 d(tgx) =
=∫tg 4 x(1+ 2tg 2 x + tg 4 x)d(tgx) = ∫tg 4 xd(tgx) + 2∫tg 6 xd(tgx) + ∫tg8 xd(tgx) =
=15 tg 5 x + 72 tg 7 x + 19 tg9 x + C
Ответ: 15 tg5 x + 72 tg7 x + 19 tg9 x + C .
Пример 46. Найти интеграл∫cosec5 xdx .
Решение
∫ cos ec |
5 |
xdx = |
используем рекурентную |
= − |
1 |
|
cos x |
+ |
3 |
∫ cos ec |
3 |
xdx = |
|
(1.5.11) |
|
= |
|
|
|||||||||||||||
формулу(1.5.11) |
|
|
||||||||||||||
|
4 |
sin4 x |
4 |
|
|
2n + 1 = 3, n = 1 |
|
|||||||||
|
|
|
2n + 1 = 5, n = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
cos x |
|
3 |
|
|
1 |
|
|
|
cos x |
|
1 |
|
|
|
|
|
|
|
1 |
|
cos x |
||||||||
= − |
|
|
|
|
|
+ |
|
− |
|
|
|
|
|
|
|
|
+ |
|
∫ cos ecxdx |
= − |
|
|
|
|
|
|||||||
4 |
sin |
4 |
x |
4 |
2 |
sin |
2 |
x |
2 |
4 |
sin |
4 |
x |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Ответ: − |
1 |
|
cos x |
− |
3 |
|
|
cos x |
+ |
3 |
ln |
|
tg |
x |
|
+ C |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
4 |
sin4 x |
|
|
sin2 x |
8 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
8 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||
Пример 47. Найти интеграл∫sec3 xdx .
Решение
− |
3 |
|
cos x |
+ |
3 ln |
tg |
x |
+ C |
|
8 |
sin 2 x |
2 |
|||||||
|
|
|
8 |
|
|
∫sec |
3 |
xdx |
= |
|
используем рекурентную |
= |
1 |
|
sin x |
+ |
1 |
∫sec xdx = |
1 |
|
sin x |
+ |
1 |
∫ |
dx |
= |
||||||||||||||||||
|
|
|
|
фомулу(1.5.10) |
2 |
|
2 |
2 |
|
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
cos2 x |
cos2 x |
cos x |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2n + 1 = 3, n = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= 1 |
|
|
sin x |
|
|
+ 1 ln |
|
tg( |
x |
+ π ) |
|
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2 |
|
2 |
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Ответ: |
1 |
|
|
|
sin x |
+ |
1 |
|
x |
+ π ) |
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
ln |
tg( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
2 |
|
2 |
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
32
1.6.Тесты (теория)
1.Дать определение первообразной.
2.Чем отличаются две первообразные для одной и той же функции?
3.Для каких функций существует первообразная на заданном интервале?
4.Что называется неопределенным интегрированием?
5.Что называется неопределенным интегралом?
6.В чем заключается основное отличие операции интегрирования от операции дифференцирования?
7.Каким знаком обозначается интеграл?
8.Какая функция называется подынтегральной функцией?
9.Какие выражения называются подынтегральными выражениями?
10.Перечислите основные свойства неопределенного интеграла?
11.Перечислите основные способы вычисления интегралов
12.Назовите основные способы вычисления интегралов?
13.В чем заключается замена переменной в неопределенном интеграле?
14.Запишите и объясните формулу интегрирования по частям.
15.Приведите пример применения формулы интегрирования по частям.
16.Что называется рациональным выражением?
17.Какая рациональная дробь называется правильной?
18.Каким образом не правильная рациональная дробь переводится в правильную?
19.Какие правильные дроби называются простейшими?
20.Сколько типов простейших дробей вы знаете?
21.Какие числа называются корнями многочлена?
22.Можно ли правильную рациональную дробь представить в виде суммы простейших дробей?
23.При каких условиях правильную рациональную дробь можно разложить на простейшую?
24.Изложите методы интегрирования простейших рациональных дробей 1, 2, 3 типов.
25.Сформулируйте теорему о разложении многочлена на простейшие множители.
26.Изложите правило разложения правильной рациональной дроби на простейшие дроби в случае простейших действительных корней знаменателя. Приведите пример.
27.Изложите правило разложения правильной рациональной дроби на простейшие дроби в случае действительных кратных корней знаменателя. Приведите пример.
28.Изложите правило разложения правильной дроби на простейшие для случая, когда среди корней знаменателя имеются пары простых комплексно-сопряженных корней.
29.Какие выражения называются иррациональными?
30.В чем состоит общая идея метода рационализации при интегрировании иррациональных и трансцендентных функций?
31.Приведите наиболее типичные случаи рационализации интегралов от иррациональных функций.
32.Какого вида интегралы от иррациональных функций сводятся к интегралам от функций, зависящих от тригонометрических функций?
33.В каких случаях интегралы от дифференциальных биномов сводятся к интегралам от рациональных функций?
34.Перечислите типы тригонометрических выражений и способы их интегрирования?
33
35.Приведите интегралы от тригонометрических функций, которые рационализируются с помощью подстановки t = sin kx и t = cos kx .
36.Интегралы какого вида от тригонометрических функций целесообразно рационализировать с помощью подстановки t = tgkx .
37.Интегралы какого вида при помощи универсальной тригонометрической подстановки сводятся к интегралу от рациональной дроби новой переменной?
38.В каких случаях можно упростить подынтегральную функцию с помощью формул понижения четных степеней синуса и косинуса?
39.При вычислении интегралов какого вида используется тригонометрические формулы преобразования произведения в сумму?
40.С помощью каких формул можно понизить степень тангенса или котангенса при интегрировании тригонометрических функций?
41.Приведите прием вычисления интегралов от нечетной положительной степени секанса или косеканса с помощью рекуррентных формул.
42.Интегралы какого вида можно упростить с помощью формул понижения четных степеней секанса и косеканса?
34
