
- •Предисловие
- •Общие рекомендации студенту заочнику
- •Работа с учебником
- •Решение типовых задач
- •Ответы на тестовые задания
- •Установочные лекции и практические занятия
- •Контрольные вопросы
- •Зачеты и экзамены
- •Требования к выполнению контрольных работ
- •1. Неопределенный интеграл
- •1.1. Основные понятия и свойства
- •1.2. Способы нахождения интегралов
- •1.2.1. Табличное интегрирование
- •1.2.2. Линейное преобразование выражения под знаком дифференциала
- •1.2.3. Подведение (внесение) под знак дифференциала
- •1.2.4. Замена переменной в неопределенном интеграле
- •1.2.5. Интегрирование по частям
- •1.3. Интегрирование рациональных выражений
- •1.4. Интегрирование иррациональных выражений
- •1.5. Интегрирование тригонометрических выражений
- •2. Определенный интеграл
- •2.1. Основные свойства и определения
- •2.2. Замена переменной в определенном интеграле
- •2.3. интегрирование по частям в определенном интеграле
- •2.4. Несобственные Интегралы
- •2.4.1. Несобственные интегралы с бесконечными пределами (I рода)
- •2.4.2. Несобственный интегралы от неограниченных функций (II рода)
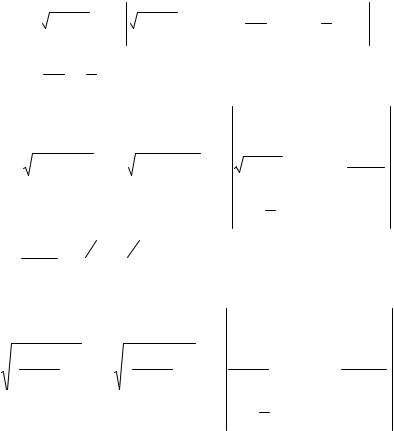
∫ |
x2 |
+ 1 |
dx = ∫ |
|
|
1 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
1 |
|
|
1 |
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
− |
|
|
|
|
+ |
|
|
|
dx = − |
|
|
+ |
|
|
− |
|
|
+ C . |
|||||
(x + 1) |
4 |
(x + 1) |
2 |
|
(x + 1) |
3 |
|
(x + 1) |
4 |
x + 1 |
(x + 1) |
2 |
3(x + 1) |
3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ответ: − |
1 |
|
+ |
1 |
|
|
|
− |
|
2 |
|
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
x + 1 |
(x + 1)2 |
|
3(x |
+ |
1)3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1.4. Интегрирование иррациональных выражений
При интегрировании иррациональных выражений (в данном случае имеется в виду выражения, содержащие корни) удается в некоторых случаях избавиться от иррациональности с помощью следующих замен:
∫ R(x1 n ax + b )dx = n ax + b = t; x = tnb |
; |
dx = n tn−1dt = |
|
|||||||
1. |
|
|
|
|
|
|
a |
|
a |
(1.4.1) |
∫ |
|
n |
|
|
∫ |
|
|
. |
||
= |
|
R * (t)dt |
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
R t b |
, t n tn−1dt = |
|
|
|
|
||||
|
|
|
a |
|
a |
|
|
|
|
|
k = HOK(n1 ,...,nr )
|
|
|
|
|
|
|
n1 |
|
|
|
m1 |
|
|
|
nr1 |
(ax |
|
|
|
|
m1r |
dx = |
|
k |
ax + b |
= t; |
x = |
tk − b |
; |
|||||||||
|
|
∫ |
|
R x |
|
(ax + b) |
,..., |
|
+ b) |
|
|
|
a |
|
||||||||||||||||||||||||
2. |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = k t k −1dt |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
tk − b |
|
|
k n |
|
|
k n |
|
|
k |
|
k−1 |
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
= |
R |
|
|
, t |
1 |
, t |
|
r |
|
|
t |
|
|
dt = |
R *(t)dt |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = HOK(n1 ,..., nr ) |
|
|
|
|
|||||||||
|
|
|
|
|
ax + b |
m1 |
|
|
|
ax + b |
mr |
|
|
|
ax + b |
|
|
|
|
|
b − t |
k |
d |
|
||||||||||||||
∫ |
R |
|
x1 |
n1 |
|
|
|
|
nr1 |
|
dx = |
|
= t |
k |
; |
x = |
|
; |
||||||||||||||||||||
|
|
|
|
|
|
|
,..., |
|
|
|
|
|
|
|
|
|
cx + d |
|
ctk − a |
|||||||||||||||||||
|
|
|
|
cx + d |
|
|
|
|
|
cx + d |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = k t k−1dt |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
=
. (1.4.2)
= ∫ (1.4.3)
|
|
|
. |
|
|
|
|
|
Здесь в пунктах 2 и 3 k |
- наименьшее общее кратное показателей корней n1 ,n2 ,..., nr . R - |
|||||||
рациональная функция. |
|
|
|
|||||
4. Интегралы от дифференциальных биномов: |
||||||||
∫ xm (a + bxn )P dx , где: |
m,n, P - рациональные числа, сводятся к интегралам от |
|||||||
рациональных дробей только в трех случаях: |
||||||||
P - целое число, тогда |
|
|
|
|||||
∫ xm |
(a + bxn )P dx = |
|
x = t k ; |
dx = ktk −1dt |
|
= ∫t mk (a + bt nk )P ktk −1 dt = ∫ R *(t)dt (1.4.4) где k - |
||
|
|
|||||||
наименьшее общее кратное дробей m и n . |
||||||||
m + 1 |
|
|
|
|||||
|
n |
- целое число; в этом случае данный интеграл рационализируется с помощью |
||||||
подстановки a + bxn = t k , где k - знаменатель дроби P . |
||||||||
m + 1 |
|
|
|
|||||
|
|
|
+ P - целое число; в этом случае интеграл рационализируется с помощью |
|||||
|
n |
|||||||
подстановки ax− n + b = tk , где k - знаменатель дроби P .
21

|
5. Интеграл вида ∫ |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
ax2 + bx + c |
приводится к табличным интегралам X и XII путем |
|
||||||||||||||||||||||||||||
выделения полного квадрата из квадратного трехчлена. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
6. Интегралы вида ∫ |
Ax + B |
|
dx путем выделения в числителе производной квадратного |
|||||||||||||||||||||||||||||
|
ax |
2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ bx + c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
трехчлена, стоящего под знаком корня распадаются на сумму двух интегралов |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
A |
(2ax + b) |
|
|
Ap |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Ax + B |
|
|
|
|
+ B − |
|
|
|
|
A |
|
d(ax |
2 |
+ bx + c) |
|
|
Ap |
|
|
|
dx |
|
||||||||||
|
|
|
2a |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
∫ |
dx = ∫ |
|
|
|
|
|
|
|
|
2a |
|
∫ |
|
|
|
|
|
||||||||||||||||
ax |
2 |
+ bx |
|
|
|
|
ax |
2 |
+ bx + c |
|
|
|
dx = |
2a |
ax |
2 |
+ bx + c |
+ |
+ B − |
2a |
∫ |
ax |
2 |
+ bx + c |
, |
||||||||
|
|
+ c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
которые фактически являются табличными интегралами. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
7. Интегралы вида ∫ |
|
|
|
|
dx |
|
|
|
|
приводятся к табличным интегралам с помощью |
|
|||||||||||||||||||||
|
(x − λ ) |
|
ax |
2 |
+ bx + c |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
подстановки x − λ = |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. Интегралы вида |
∫ |
Pn (x)dx |
|
dx , где P (x) |
- многочлен n ой степени, находятся с |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
ax2 + bx + c |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
помощью тождества: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
Pn (x)dx |
|
dx = Q |
n−1 |
(x) |
ax2 + bx + c + λ |
|
|
dx |
|
|
|
|
(1.4.5), |
|||||||||||
|
|
|
|
|
∫ ax2 + bx + c |
|
|
|
|
|
|
|
|
|
∫ ax2 |
+ bx + c |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
где Q |
(x) - многочлен (n −1) й |
степени с неопределенными коэффициентами, λ - число. |
|
|||||||||||||||||||||||||||||
|
|
|
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференцируя указанное тождество (1.4.5) и приводя результат к общему знаменателю, |
|
|||||||||||||||||||||||||||||||
получим равенство двух многочленов, из которого можно определить коэффициенты |
|
|
|||||||||||||||||||||||||||||||
многочлена Qn−1 (x) и число λ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
9. Интегралы вида ∫ R(x1 |
|
a2 − x2 )dx, |
|
∫ R(x1 |
a2 + x2 )dx, ∫ R(x1 |
x2 − a2 )dx с помощью |
|
|||||||||||||||||||||||||
надлежащих тригонометрических подстановок сводятся к интегралам от функций, рационально зависящих от тригонометрических функций:
∫ R(x1 |
a2 − x2 )dx = |
|
x = asin t; |
dx = acostdt |
|
|
= ∫ R(a cost) acost dt ; |
(1.4.6) |
||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
∫ |
R(x |
|
|
2 |
|
|
2 |
)dx = |
|
x = a tgt; |
|
|
a |
|
|
|
|
|
|
|
∫ |
|
a |
|
|
a |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
a |
|
+ x |
|
|
dx = |
|
|
dt |
= |
R |
|
|
|
|
|
dt ; |
(1.4.7) |
|||||||||||||||||||||||
|
|
cos2 t |
|
|
cos2 t |
|||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
)dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cost |
|
|
|
|
|||||||||||
∫ |
R(x x |
2 |
|
|
2 |
|
|
|
|
|
|
|
a |
|
|
|
asin t |
|
|
|
|
|
|
∫ |
|
|
sin t |
|
asin t |
dt |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
− a |
|
x = |
|
|
|
|
; |
dx = |
|
|
dt |
= |
R a |
|
|
|
|
|
(1.4.8) |
||||||||||||||||||||
|
|
|
cost |
cos2 t |
cost |
cos2 t |
||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 21. Найти интеграл: ∫ |
|
|
|
|
dx |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
x |
+ |
3 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение:
22
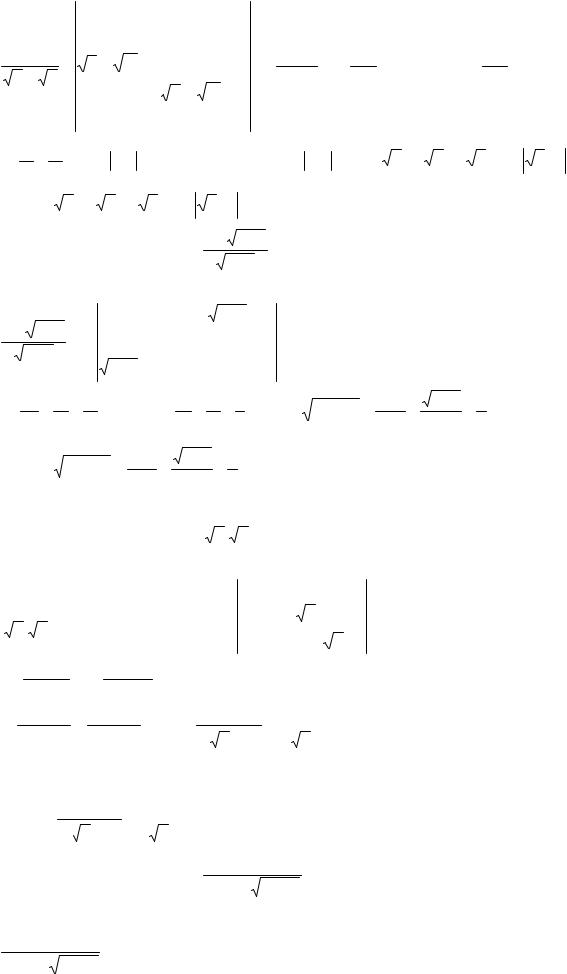
|
|
|
|
|
|
|
|
HOK(2,3) = 6; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
dx |
|
|
|
|
x = t6 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6t5dt |
|
t |
3dt |
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||||||||||
∫ |
|
|
|
|
|
= x |
= |
|
t |
6 |
= t |
3 |
; |
|
|
|
|
|
|
|
|
= ∫ |
|
= 6∫ |
|
|
|
|
2 |
− t |
+ 1− |
|
||||||||||||||||||||||
x + |
3 |
x |
|
|
|
|
|
|
|
|
|
|
|
t |
3 |
+ t |
2 |
t |
+ 1 |
= 6∫ t |
|
|
|
|
dt |
|||||||||||||||||||||||||||||
|
|
|
dx |
= 6t5dt; |
|
|
3 x = 3 t6 = t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
t + 1 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
t3 |
− |
t 2 |
+ t − ln t + 1 |
|
+ C = 2t3 − 3t 2 + 6t − 6ln t + 1 + C = 2 x − 33 x + 66 x − 6ln 6 |
||||||||||||||||||||||||||||||||||||||||||||||||
= 6 |
3 |
|
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
2 |
|
x − 33 |
x + 66 |
x − 6ln 6 |
x + 1 + C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Пример 22. Найти интеграл: ∫ x +3 |
1 |
1+ x dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x + 1+ x |
|
|
HOK(2,3) = 6; |
|
|
1+ x = t3 |
|
|
|
|
(t6 |
−1)+ t |
3 |
|
|
|
|
|
|
|
6∫(t |
|
|
|
|
|
|
)dt |
|||||||||||||||||||||||||
∫ |
dx = |
1+ x = t |
6 |
; |
|
|
x = t |
2 |
−1; |
|
|
|
|
= ∫ |
|
6t |
5 |
dt = |
9 |
+ t |
6 |
|
− t |
3 |
||||||||||||||||||||||||||||||
3 1+ x |
|
|
|
|
|
|
|
|
|
|
|
t 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 1+ x = t 2 ; dx = 6t5dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
t10 |
|
+ |
|
t |
|
t4 |
|
|
|
|
|
6t |
4 t6 |
+ |
t3 |
− |
1 |
|
|
|
= 63 (1+ x) |
2 |
|
|
|
1+ x |
+ |
|
1+ x |
− |
1 |
|
|
|
|||||||||||||||||||
= 6 |
|
|
|
|
− |
|
+ C = |
|
|
|
|
|
|
|
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ C |
|||||||||||||||||||||||||
|
|
10 7 4 |
|
|
|
|
|
|
|
|
|
10 7 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
7 |
|
|
4 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Ответ: |
63 |
(1+ x) |
2 |
|
1+ x |
+ |
1+ x |
− |
1 |
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
7 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
=
.
x + 1 + C
=
.
Пример 23. Найти интеграл: ∫ |
|
|
dx |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x(4 |
x + 1)10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
dx |
|
|
|
|
|
− 1 |
|
1 |
|
|
−10 |
|
|
P = −10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
∫ |
|
|
|
|
|
∫ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
= |
|
|
|
x |
|
+ 1 dx = x = t4 ; |
x = t2 |
|
|
= |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
x(4 x + 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = 4t |
3dt; 4 x = t |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
dt |
|
− 4∫ |
|
dt |
|
|
|
|
|
|
|
|
|
|
−9 |
|
|
|
− 4∫ (t + |
|
|
−10 |
|
|
|
|
|
|
|
|
|
||||||
= 4∫ (t + 1)9 |
(t + 1)10 = 4∫ (t + 1) |
|
d(t |
+ 1) |
1) |
|
|
d(t + 1) |
= . |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
2(t + 1)8 |
+ 9(t + 1)9 + C = − |
2(4 x + 1)8 |
+ |
|
|
+ C |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
9(4 x + 1)9 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
P = −10 - целое число (случай 1) интегрируемости дифференциального бинома (п. 4) |
|
|
||||||||||||||||||||||||||||||||||||||
(1.4.4)). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: − |
|
1 |
|
+ |
|
|
|
|
4 |
|
|
|
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2(4 x + 1)8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
9(4 |
x + 1)9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Пример 24. Найти интеграл: |
∫ |
|
|
x3dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
(4 − x2 ) |
4 − x2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∫ |
|
|
x3dx |
|
|
|
= ∫ x |
3 |
(4 − x |
2 |
− |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
m + 1 |
|
3 + 1 |
|
|
||||||||
|
|
|
|
|
2 dx имеем |
m = 3, |
|
n = |
2, P = − |
, так как |
= |
= 2 |
- |
|||||||||||||||||||||||||||
(4 |
− x |
2 |
) 4 |
− x |
2 |
|
|
|
) |
|
2 |
n |
2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
целое число, то имеем случай 2) интегрируемости дифференциального бинома (п. 4).
23
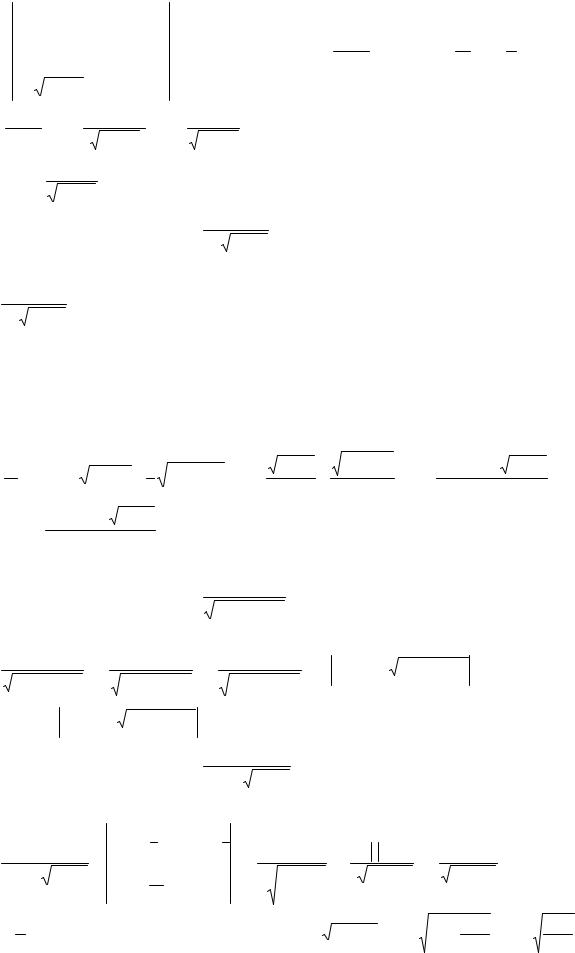
|
|
4 − x2 = t 2 ; x2 = 4 − t 2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
− 2xdx = 2tdt; |
|
|
= −∫ |
(4 − t |
2 |
) t |
−3 |
tdt = − ∫ |
4 − t2 |
|
|
|
dt |
4 |
|
||||||||
|
xdx = −tdt; |
|
|
|
|
|
|
t 2 |
dt = ∫dt − 4∫ t2 |
= t + t |
+ C = |
||||||||||||||
|
|
t = |
4 − x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
t |
2 + 4 |
+ C = |
4 − x2 + |
4 |
+ C = |
8 |
− x2 |
|
+ C |
|
|
|
|
|
|
|
|
|||||||
|
t |
4 − x2 |
|
4 − x2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: |
8 − x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
4 − x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 25. Найти интеграл: ∫ |
|
|
dx |
|
2 . |
|
|
|
|
|
|
|
|||||||||||||
x |
4 |
1 |
+ x |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∫ |
|
4 dx |
|
2 = |
∫ x−4 (1+ x2 )− |
1 |
dx имеем m = −4, |
n = 2, |
P = − |
1 |
; |
m + 1 |
+ P = −2 - целое |
||||||||||||
|
|
2 |
|||||||||||||||||||||||
x |
|
2 |
n |
||||||||||||||||||||||
|
1+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
число, то имеем случай 3) интегрируемости дифференциального бинома (п. 4). Полагаем, что
x−2 + 1 = t 2 |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
− 2x−3dx = 2tdt |
|
èëè |
x−3dx = −tdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∫ x−4 [x2 (x−2 + 1)]− |
|
dx = ∫ x−2 (x−2 + 1)− |
|
|
x−3dx = ∫(t2 −1) t |
−1 tdt = −∫(t 2 −1)dt = |
|
|
|||||||||||||||||||||||||||||||||||||||
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
2 |
|
. |
|||||||||||||||||||||||||||||||||||||||||||||
− t3 |
|
|
|
|
|
|
|
|
|
+ 1 − 1 |
(x−2 + 1)3 + C = |
1+ x2 − |
(1+ x2 )3 |
+ C = (2x2 − |
1) |
1+ x2 |
|||||||||||||||||||||||||||||||
+ t + C = x−2 |
+ C |
||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
3x3 |
|
|
|
|
|
|
3x3 |
|
|
|
||||||||
Ответ: |
(2x2 −1) |
1+ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
3x3 |
|
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 26. Найти интеграл: ∫ |
|
|
|
dx |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
x |
2 |
+ 4x + |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∫ |
|
|
|
dx |
|
= ∫ |
|
|
dx |
|
= |
∫ |
|
d(x + 2) |
|
|
= ln (x + 2) + |
x |
2 |
+ 4x + 9 + C . |
|
|
|
||||||||||||||||||||||||
x |
2 |
+ 4x + |
|
2 |
+ 5 |
|
(x + |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
9 |
|
|
|
(x + 2) |
|
|
|
|
2) |
+ 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Ответ: ln (x + 2) + |
x2 + 4x + 9 + C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Пример 27. Найти интеграл: ∫ |
|
|
|
dx |
|
|
|
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
(x − |
1) 1− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
dx |
|
|
|
|
x −1 = t ; x = 1 |
+ t |
|
|
|
|
|
|
|
|
− |
|
|
|
|
t dt |
|
|
|
|
dt |
|
|
|
|
|
|||||||||||||
∫ |
|
|
|
|
|
= |
= ∫ |
|
|
|
|
|
t2 |
− ∫ |
|
|
|
= ∫ |
|
|
= |
|
|
||||||||||||||||||||||||
(x −1) 1− x |
2 |
|
1 |
|
|
|
|
|
1 |
|
|
|
1+ 2t |
t |
− t − 2t |
−1 |
− |
2t |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dx = − t 2 |
dt |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= − |
1 |
∫(−1− |
|
− |
1 |
d |
(−1− 2t) = −(−1− 2t) |
1 |
|
+ C = C − −1− 2t = C − −1− |
|
2 |
|
= C − |
|
x + 1 |
|||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
2 |
2t) |
2 |
|
|
x −1 |
1− x |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
24

|
Здесь учтено, что t 2 = t |
, что подынтегральная функция определена в интервале |
||||||||||||||||||||
−1 < x < 1, вследствие чего x −1 < 0 и t < 0 и поэтому |
|
t |
|
= −t . |
||||||||||||||||||
|
|
|||||||||||||||||||||
Ответ: C − |
|
x + 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 28. Найти интеграл: ∫ |
2x2 |
− 4x + 5 |
dx . |
|
|
|
|
|
|
|
||||||||||||
x |
2 |
+ 2x |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫ |
2x2 |
− 4x + 5 |
dx = (Ax + B) x |
2 |
+ 2x + λ ∫ |
|
dx |
= I . |
|
|||||||||||||
x |
2 |
+ 2x |
|
|
x |
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 2x |
|
||||||||
Для определения постоянных A, B,λ дифференцируем обе части равенства и затем |
||||||||||||||||||||||
умножаем на |
x2 + 2x : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2x2 − 4x + 5 |
= A x |
2 |
+ 2x + (Ax + B) |
|
|
(x + 1) |
+ |
|
λ |
; |
||||||||||||
|
x2 + 2x |
|
|
|
|
|
x2 + 2x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 + 2x |
|
|
|
|||||||||
2x2 − 4x + 5 = A(x2 + 2x) + ( Ax + B)(x + 1) + λ = 2Ax2 + x(3A + B) + (B + λ ) .
Сравнивая коэффициенты при одинаковых степенях в обеих частях последнего равенства, получаем систему уравнений и решаем ее:
x2 |
2 |
2A; |
A = 1 |
x1 |
− 4 3A + B; B = −7 . |
||
x0 |
5 |
B + λ; λ = 12 |
|
Подставляем значения коэффициентов A, B,λ в схему интегрирования:
I = (x − 7) |
x |
2 |
+ 2x + 12∫ |
|
dx |
|
. |
|
|
|
|
|
|||||||||
|
x |
2 |
+ |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|||
Преобразуем последний интеграл: |
|
|
|
|
|
||||||||||||||||
∫ |
|
dx |
|
= ∫ |
|
dx |
|
|
= ln x + 1+ (x + 1) |
2 |
−1 |
+ C . |
|||||||||
x |
2 |
+ 2x |
(x + 1) |
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
||||||
Окончательно получаем: |
|
|
|
|
|
|
|
|
|
|
|||||||||||
I = ∫ |
2x2 − 4x + 5 |
dx = (x − |
7) x |
2 |
+ 2x + 12ln x |
+ 1+ |
x |
2 |
+ 2x + C |
||||||||||||
|
x |
2 |
+ |
2x |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: (x − 7) x2 + 2x + 12 ln x + 1+
x2 + 2x + 12 ln x + 1+  x2 + 2x + C .
x2 + 2x + C .
Пример 29. Найти интеграл: ∫ |
(4 − x2 )3 |
||
x |
2 |
dx . |
|
|
|
|
|
Решение:
25
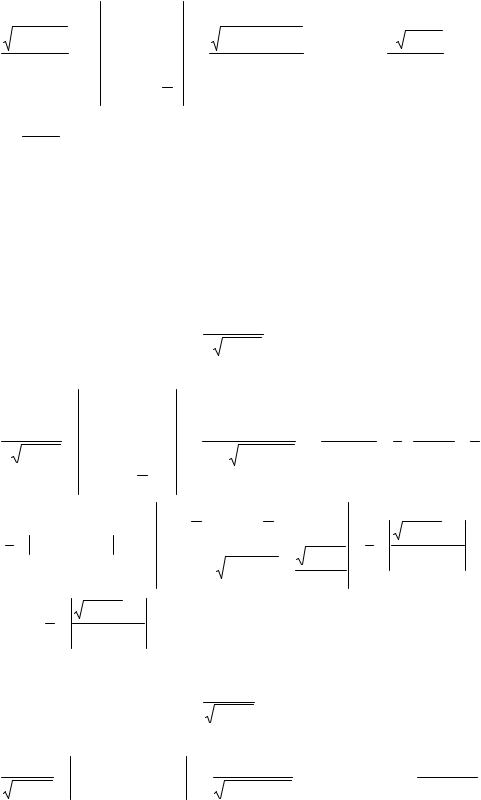
∫ |
|
(4 − x2 )3 |
|
x = 2sin t |
|
|
(4 − 4sin 2 t)3 |
|
|
|
|
8 |
cos6 t |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
x2 |
|
|
dx = dx = 2costdt = ∫ |
|
|
4sin 2 t |
|
|
|
2costdt = ∫ 4sin 2 t |
2costdt = |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
t = arcsin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos4 t |
|
|
(1− sin 2 t)2 dt |
|
|
|
(1− 2sin 2 t + sin 4 t) |
|
|
|
dt |
|
|
|
|
|
2 |
|
|
. |
||||||||||||||||||
= |
4∫ sin 2 t |
dt = 4∫ |
|
|
|
|
|
= 4∫ |
|
|
|
|
|
|
dt |
= 4∫ |
|
− 8∫dt + 4∫sin |
|
tdt |
= |
||||||||||||||||||||
|
|
|
sin 2 t |
|
|
sin 2 t |
|
|
sin 2 t |
|
|||||||||||||||||||||||||||||||
= −4ctgt − 8t |
+ 4 1 ∫(1− cos 2t)dt = |
4ctgt − 8t + 2t − sin 2t + C = 4ctg arcsin |
x |
|
− 6arcsin |
x |
− |
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|||
− sin 2arcsin |
x |
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
4ctg arcsin |
x |
|
− 6arcsin |
x |
− sin 2arcsin |
x |
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 30. Найти интеграл: ∫ |
|
|
dx |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x |
9 + x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
dx |
|
|
|
x = 3tgt |
|
|
|
|
|
3sec2 t dt |
|
|
|
|
|
sec2 tdt |
= 1 |
∫ sectdt = |
1 |
|
|
|
|
|
|
|||||||||||||
∫ |
|
|
|
2 = dx = 3sec2 t dt = ∫ |
|
2 |
t |
= ∫ |
|
∫dt sin t = |
|
||||||||||||||||||||||||||||||
|
x 9 + x |
|
|
t = arctg x |
|
|
|
3tgt |
9 + 9tg |
|
|
|
|
3tgt sect |
3 |
tgt |
|
3 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
tgt = x |
; |
ctgt = 3 |
|
|
|
|
|
|
|
1 |
|
|
x2 + 9 |
− 3 |
|
|
|
|
|
|
|
|
||||||
= |
|
ln cosect − ctgt + C = |
3 |
|
|
|
|
x |
|
|
|
|
|
= |
ln |
+ C |
|
|
|
|
|||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
x |
2 |
3 |
x |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
cosect = |
|
1+ ctg 2t = |
+ 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: |
1 |
ln |
|
x2 + 9 − 3 |
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 31. Найти интеграл: ∫ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x |
2dx . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
− |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∫ |
x2 dx |
= |
x = 2sect; |
|
|
= |
∫ |
4sec2 t |
2sect tgt dt = 4∫ |
sec3 t tgt |
dt |
||||||||||||||
x |
2 |
− |
dx = 2sect tgt dt |
4sec |
2 |
t − 4 |
tgt |
||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Используем рекуррентную формулу (1.4.9): |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
∫ |
|
2n+1 |
|
|
1 |
|
sin t |
|
|
1 |
∫ |
|
2n−1 |
|
||||||
|
|
|
|
|
sec |
|
t |
dt |
= |
|
|
|
|
|
|
+ 1 |
− |
|
|
sec |
|
t dt |
|
||
|
|
|
|
|
|
|
2n |
cos2n t |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
|
|
|
|
|||||||
= 4∫sec3 tdt
(1.4.9.);
Тогда имеем: |
|
|||||
|
|
1 |
|
sin t |
|
|
4 |
|
|
|
|
|
|
2 |
cos |
2 |
t |
|||
|
|
|
|
|||
|
1 |
|
|
sin t |
|
|
1 |
|
dt |
|
sin t |
|
|
1 |
|
|
|
||
+ |
|
∫sect dt |
= 2 |
|
|
|
+ |
|
∫ |
|
= 2 |
|
|
|
+ |
|
ln |
sect + tgt |
+ C = I . |
2 |
|
2 |
t |
2 |
cost |
|
2 |
t |
2 |
||||||||||
|
|
|
cos |
|
|
|
|
cos |
|
|
|
|
|
||||||
26
