
- •Предисловие
- •Общие рекомендации студенту заочнику
- •Работа с учебником
- •Решение типовых задач
- •Ответы на тестовые задания
- •Установочные лекции и практические занятия
- •Контрольные вопросы
- •Зачеты и экзамены
- •Требования к выполнению контрольных работ
- •1. Неопределенный интеграл
- •1.1. Основные понятия и свойства
- •1.2. Способы нахождения интегралов
- •1.2.1. Табличное интегрирование
- •1.2.2. Линейное преобразование выражения под знаком дифференциала
- •1.2.3. Подведение (внесение) под знак дифференциала
- •1.2.4. Замена переменной в неопределенном интеграле
- •1.2.5. Интегрирование по частям
- •1.3. Интегрирование рациональных выражений
- •1.4. Интегрирование иррациональных выражений
- •1.5. Интегрирование тригонометрических выражений
- •2. Определенный интеграл
- •2.1. Основные свойства и определения
- •2.2. Замена переменной в определенном интеграле
- •2.3. интегрирование по частям в определенном интеграле
- •2.4. Несобственные Интегралы
- •2.4.1. Несобственные интегралы с бесконечными пределами (I рода)
- •2.4.2. Несобственный интегралы от неограниченных функций (II рода)
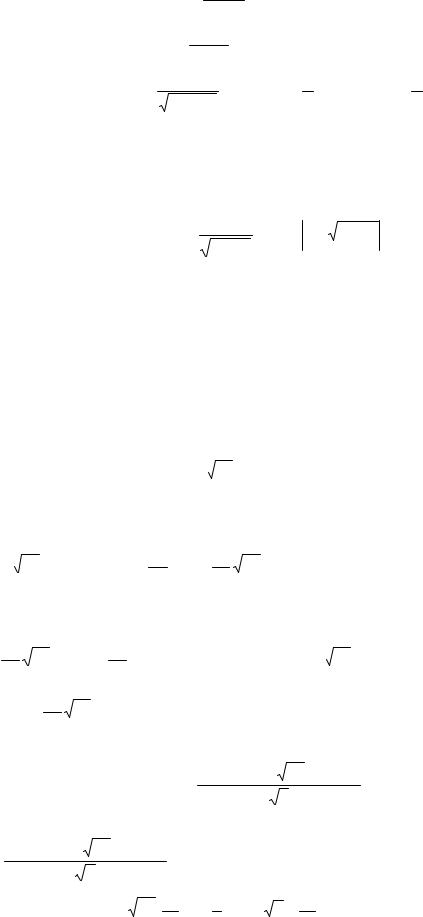
∫cos udu = sin u + C .
∫cos12 udu = ∫sec2udu = tgu + C .
∫sin12 udu = ∫cos ec2udu = −ctgu +С .
∫ |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
u |
|
|
|||
|
a2 − u2 |
du = arcsin a |
+ C = − arccos a |
+ С. |
||||||||||||||||||||||||
∫ |
|
|
1 |
|
|
du |
= |
1 |
arctg |
u |
+ C = − |
1 |
arcctg |
u |
|
+ C . |
||||||||||||
u |
2 |
+ a |
2 |
|
|
|
|
|
|
a |
||||||||||||||||||
|
|
|
|
|
|
|
a |
a |
|
|
|
|
a |
|
|
|||||||||||||
|
|
|
|
|
∫ |
|
|
1 |
|
|
du = |
|
1 |
|
a + u |
|
+ C . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|||||||||||||||
|
|
|
|
|
a |
2 |
− u |
2 |
|
2a |
a − u |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ u 2 + b du = ln u |
+ |
u |
|
+ b |
+ C . |
|
|
|||||||||||||||||
(1.1.13)
(1.1.14)
(1.1.15)
(1.1.16)
(1.1.17)
(1.1.18)
(1.1.19)
Каждая из формул приведенной таблицы справедлива на любом отрезке, находящегося в области определения соответствующей подынтегральной функции.
1.2. Способы нахождения интегралов
1.2.1. Табличное интегрирование
Интегрирование с помощью свойств неопределенного интеграла и таблицы основных интегралов элементарных функций.
Пример 1. Найти интеграл: ∫64 x3 dx и проверить дифференцированием полученный результат.
Решение:
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
dx = 6 x 4 |
|
|
|
|
24 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
∫64 x3 dx = 6∫ x |
|
+ C = |
x7 + C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Проверка: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
24 4 |
|
|
7 |
|
|
|
|
|
|
24 |
|
7 |
|
|
|
|
|
|
|
|
|
24 |
|
7 |
|
3 |
|
|
|
3 |
|
4 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
x |
|
+ C |
' |
= |
|
x 4 + C |
' = |
|
|
|
|
|
|
x 4 = 6x 4 |
= 6 |
|
|
x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
7 |
|
7 |
7 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Ответ: |
24 4 |
x7 |
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Найти интеграл: ∫ |
x4 − 3x2 + 53 x |
2 − 7x + 6 |
dx . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x − 3x2 + 53 x2 − 7x + 6 |
|
|
|
|
|
11 |
|
|
|
|
5 |
|
|
|
|
|
2 |
|
|
|
|
− |
1 |
|
|
3 |
14 |
|
9 |
8 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
∫ |
dx = |
∫(x 3 − 3x 3 + 5 |
− 7x |
3 + 6x |
3 )dx = |
x 3 |
− |
x 3 + 5x |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
x |
|
|
|
|
|
|
|
|
|
|
14 |
8 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||
|
21 |
5 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
− |
5 |
x 3 + 9x 3 + C = |
|
x |
|
(14 x |
|
− |
8 x |
|
|
+ 53 x − |
5 x |
+ 9) + C |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
9
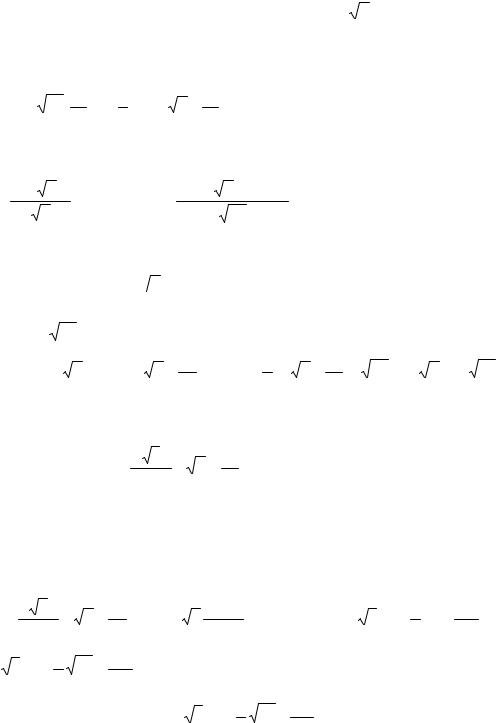
Указание:
в данном интеграле числитель делим на знаменатель 3 x почленно и затем интегрируем.
при вычислении интеграла от суммы нескольких функций сумму произвольных постоянных, которая при этом получается, заменяют одной произвольной постоянной, обозначаемой обычно буквой С.
Ответ: |
3 |
x |
2 |
( |
3 |
x |
4 |
− |
9 |
x |
2 |
3 |
x − |
21 |
x + 9) |
+ C . |
|||||
|
|
14 |
|
8 |
|
+ 5 |
5 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 3. Найти интегралы: |
|
|
|
|
|
|
|
||||||||||||||
1) ∫ |
(1+ |
|
x)3 |
dx ; |
|
|
|
|
|
2) ∫ |
(4 + 2 x)(x3 + 3) |
dx . |
|||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
3 |
x |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Указание:
в первом интеграле необходимо сначала числитель возвести в куб, полученный многочлен разделить на знаменатель  x и после этого проинтегрировать;
x и после этого проинтегрировать;
во втором интеграле в числителе перемножить многочлены, произведение разделить на знаменатель 3 x2 , после чего выполнить интегрирование.
Ответ: 1) 2 x + 3x + 2x x + x2 |
+ C ; 2) |
∫ 6 x3 3 |
x + |
12 x3 6 |
x5 + 603 |
x + 126 x5 + C . |
2 |
|
5 |
|
23 |
|
|
Пример 4. Найти интегралы, используя свойства неопределенных интегралов:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
3 |
|
x |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
∫ |
cos |
2 |
x |
|
|
|
x |
4 dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1) ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
x |
+ |
|
|
dx ; 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||||||||
1) ∫ |
x |
+ |
|
|
|
dx = ∫ |
x |
|
|
+ 2 |
|
|
|
x + |
|
|
|
|
dx |
= |
|
|
|
|
|
|
+ 4x − |
|
+ C . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
x |
|
|
|
x |
x |
2 |
|
|
|
3 |
|
x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∫ |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
−4 |
3 |
|
4 |
|
2 |
|
|
|||||||||
|
|
|
|
|
− |
|
|
x |
− |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
− x3 |
+ |
2x |
x 3 − |
|
+ C = |
|||||||||||||||||||||||||||||||||
|
|
|
|
2 |
x |
3 |
x |
4 |
|
|
dx |
= ∫ |
|
|
cos |
2 |
x |
|
dx = 3tgx − |
4 |
3x |
3 |
|||||||||||||||||||||||||||||||||||||||||||
2) |
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||
|
3tgx − |
3 3 |
|
x4 |
− |
|
2 |
|
|
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
3x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ответ: 1) |
|
|
x3 |
+ 4x − |
|
4 |
|
+ C ; 2) |
|
|
3tgx − |
3 3 |
x4 |
− |
2 |
|
+ C . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
x |
|
|
4 |
|
|
3x3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пример 5. Найти интегралы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1) ∫ |
|
dx |
|
|
|
|
; 2) |
∫ |
|
|
|
dx |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4x |
2 |
+ 1 |
x |
2 |
− |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1) ∫ |
|
dx |
|
|
|
|
= |
1 |
∫ |
|
|
|
|
dx |
|
|
|
|
= |
|
1 |
|
|
1 |
|
arctg |
|
x |
|
+ C = |
|
1 |
arctg2x + C . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
4x |
2 |
+ 1 |
4 |
|
x |
2 |
+ |
|
|
1 |
|
4 |
|
|
1 |
|
|
1 |
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2) ∫ |
|
dx |
|
|
|
= |
|
|
1 |
|
|
|
x − 5 |
|
+ C = |
|
1 |
|
ln |
|
|
x − 5 |
|
|
+ C . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
x |
2 |
|
|
|
|
2 5 |
x + 5 |
|
10 |
|
|
x + 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
− 25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
10
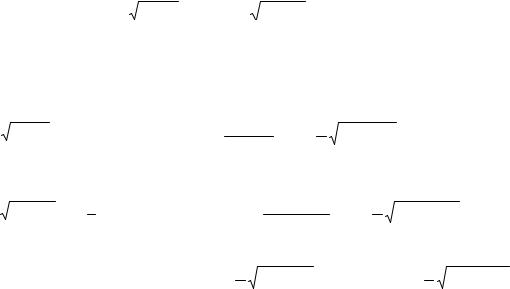
Ответ: 1) |
1 |
arctg2x + C ; 2) |
|
1 |
|
x − 5 |
|
+ C |
|
ln |
|
||||||||
2 |
10 |
x + 5 |
|||||||
|
|
|
|
|
|||||
1.2.2. Линейное преобразование выражения под знаком дифференциала
Если известен интеграл ∫ f (x)dx = F(x) + C , то следующие интегралы могут быть вычислены с помощью линейного преобразования выражения под знаком дифференциала:
|
|
|
|
|
|
|
|
|
|
|
|
1. ∫ f (x + b)dx = ∫ f (x + b)d(x + b) = F(x + b) + C . |
|
|
(1.2.1) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2. ∫ f (ax)dx = |
1 |
∫ f (ax)d(ax) = |
1 |
|
F(ax) + C . |
|
|
|
(1.2.2) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
3. |
∫ f (ax + b)dx = |
1 |
|
∫ |
f (ax + b)d(ax + b) = |
1 |
F(ax + b) + C . |
|
(1.2.3) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|||
Пример 6. Найти интеграл: ∫sin(7x − 8)dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫sin(7x − 8)dx = |
1 ∫sin(7x − 8)d(7x − 8) |
= − |
1 cos(7x − 8) + C . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: − |
1 |
cos(7x − 8) + C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 7. Найти интегралы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1) ∫2x(x2 + 8)3 dx ; 2) ∫2x x2 + 9dx ; 3) ∫ x2 3 x3 + 16dx . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) ∫2x(x2 + 8)3 dx = ∫(x2 + 8)3 d(x2 + 8) |
= 1 |
(x2 + 8)4 + C . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
d(x2 + 9) = x |
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ 9 2 |
|
+ C = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2) ∫2x x2 + 9dx = ∫(x2 + 9) |
|
|
|
|
|
|
|
(x2 + 9)3 + C . |
|
|
|
|||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 (x3 + 16) 3 |
|
|
|
|
|
|
|
1 3 (x3 |
|
|
|
|
|||||||||||
3) ∫ x2 3 x3 + 16dx = |
1 ∫(x3 + 16) |
|
d(x3 + |
16) |
= |
|
+ C = |
+ 16)4 + C . |
|
|||||||||||||||||||||||||||||||||||||||||
3 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 1) |
|
|
1 |
|
(x2 |
+ 8)4 + C ; |
|
|
|
|
|
|
|
|
2) |
2 |
|
(x2 + 9)3 + C ; |
|
|
|
3) |
1 3 |
(x3 |
+ 16)4 |
+ C . |
||||||||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|||||
Пример 8. Найти интегралы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1) ∫ |
|
|
1 |
|
|
dx ; |
|
|
2) ∫ |
|
|
sin 2x |
dx ; |
|
|
|
|
|
|
|
|
3) ∫ |
1 |
|
|
|
dx ; |
|
|
|
|
|||||||||||||||||||
|
2x + b |
|
|
1 |
+ cos 2x |
|
|
|
|
|
|
|
|
b − 3x |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
4) ∫ |
|
|
x3 |
|
|
|
|
|
dx ; |
5) ∫ |
|
|
|
e2 x |
|
|
dx ; |
|
|
|
|
|
|
|
6) |
|
∫ |
1 |
|
|
dx . |
|
|
|
|
|||||||||||||||
14 |
+ 3x |
4 |
|
25 + e |
2 x |
|
|
|
|
|
|
|
|
x ln |
3 |
x |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) ∫ |
|
|
1 |
|
|
dx = |
1 ∫ |
d(2x + b) |
|
= |
|
1 ln(2x + b) + C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
2x + b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
2x + b |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
11
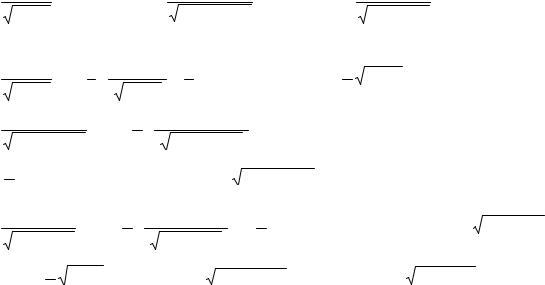
2) |
|
∫ |
|
|
sin 2x |
|
|
|
dx = − |
1 |
∫ |
d(1 + cos 2x) |
|
= − |
1 ln(1 + cos 2x) + C . |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
1 |
+ cos 2x |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + cos 2x |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
3) |
|
∫ |
|
|
1 |
|
|
|
dx = − |
1 |
∫ |
d(b − 3x) |
|
= − |
1 ln(b − 3x) + C . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
b − 3x |
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b − 3x |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4) ∫ |
|
|
x3 |
|
|
|
|
|
|
dx |
= |
|
1 |
∫ |
d(14 + 3x4 ) |
|
= |
|
|
|
1 |
|
|
|
ln |
|
14 + 3x |
4 |
|
+ C . |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
14 + |
3x |
4 |
|
|
12 |
14 + 3x |
4 |
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
5) ∫ |
|
|
e2 x |
|
|
|
|
|
dx = |
|
1 |
∫ |
|
d(25 + e2 x ) |
= |
|
1 |
|
|
ln |
|
|
25 + e |
2 x |
|
+ C . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
25 + e |
2 x |
|
2 |
|
|
25 + e |
2 x |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
6) |
∫ |
|
|
1 |
|
|
|
dx = |
∫ |
|
d(ln x) |
= ∫ln |
−3 |
xd(ln x) |
= − |
|
|
|
|
|
1 |
|
|
+ C . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
x ln |
3 |
x |
|
|
|
|
ln |
3 |
x |
|
|
2 ln |
2 |
|
x |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Ответ: 1) |
|
|
1 |
ln(2x + b) + C ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) − |
1 |
ln(1+ cos 2x) + C ; |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4) |
|
1 |
ln |
|
14 + 3x4 |
|
+ C ; |
|
|
|
|
|
|
|
5) |
|
|
1 |
ln |
|
25 + e2 x |
|
|
|
+ C ; |
|
|
|
6) − |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
12 |
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пример 9. Найти интегралы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1) |
|
∫ |
|
|
x2 |
|
|
|
|
dx ; |
|
|
|
|
|
|
|
|
|
|
|
|
2) ∫ |
|
|
sin x |
|
|
|
|
|
|
dx |
; |
|
|
|
|
|
|
|
3) ∫ |
sin x cos x |
dx |
||||||||||||||||||||||
|
|
|
1 + x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− sin |
2 |
x |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 + 2 cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Решение:
3) − |
|
1 |
ln(b − 3x) + C ; |
||
3 |
|||||
|
|
|
|||
1 |
|
+ C . |
|||
2 ln2 x |
|
||||
.
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
∫ |
|
3 dx = |
1 ∫ d(1 |
+ x3 ) |
= 1 ∫(1 + x3 ) |
− |
|
d(1 + x3 ) = |
2 |
|
1 + x3 + C . |
|
|
|
||||||||||||||||||||
|
2 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
1 + x |
|
|
|
|
3 |
|
|
1 + x |
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||
|
∫ |
|
sin x |
|
|
dx = − |
1 |
∫ d(15 + 2 cos x) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2) |
|
15 + 2 cos x |
|
|
|
|
2 |
|
15 + 2 cos x |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
− |
1 ∫(15 + 2 cos x)− |
|
d(15 + 2 cos x) = 15 + 2 cos x + C |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
sin x cos x |
|
|
|
|
1 |
∫ |
d(2 − sin 2 x) |
|
|
1 |
∫(2 − sin |
2 |
|
|
− |
1 |
|
|
2 |
|
|
2 |
|
||||||||||
3) |
dx = − |
= − |
x) |
2 d(2 − sin |
x) = − 2 |
− sin |
x + C . |
||||||||||||||||||||||||||||
2 − sin |
2 |
x |
2 |
2 |
− sin |
2 |
x |
2 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ответ: 1) |
2 |
|
1+ x3 |
+ C |
; |
|
2) |
|
15 + 2 cos x + C ; |
|
|
|
|
|
3) − |
2 − sin2 x + C . |
|
|
|||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.2.3. Подведение (внесение) под знак дифференциала
Один из множителей подынтегральной функции можно подвести под знак дифференциала. Для этого необходимо вычислить первообразную этого множителя и записать ее под знаком дифференциала.
В дальнейшем все дополнительные вычисления и рассуждения будем записывать между двумя вертикальными чертами.
∫[f (Y '(x)) Y '(x)]dx = ∫[f (Y (x))]dY (x) = F(Y (x)) + C |
(1.2.4) |
Совет. Если после внесения одного из множителей под знак дифференциала возникли затруднения в дальнейших действиях, смело заменяйте полученное выражение под знаком дифференциала на новую переменную.
Пример 10. Найти интегралы:
12
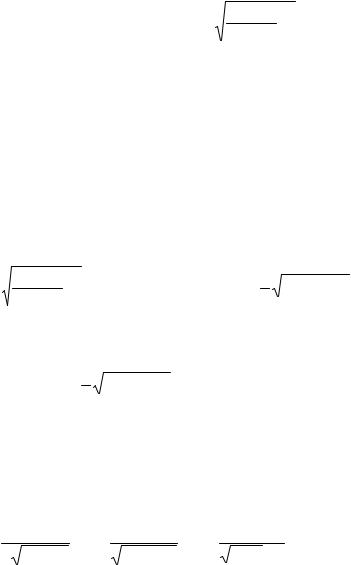
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
1) |
|
∫sin 5 x cos xdx ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) cos8 9x sin 9xdx ; |
|
|
|
|
|
|
3) ∫ |
|
acrtg x |
dx ; |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + x |
|
|
|
|
|||
4) |
|
∫ |
ln 2 x |
dx |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5) ∫ |
arcsin2 x dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1) |
|
∫sin5 xcos xdx = ∫sin5 xd(sin x) = sin6 x + C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) |
cos8 9xsin 9xdx = − |
1 |
∫cos8 9xd(cos9x) = − |
1 |
cos9 9x |
+ C = − |
1 |
|
|
cos9 |
9x + C . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
81 |
|
|
|
|
|
|
|
|
||||||||||||||
3) |
∫ |
acrtg 7 x |
dx = ∫arctg |
7 |
xd(arctgx) = |
arctg8 x |
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
1+ x2 |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
4) |
|
∫ ln2 x dx = ∫ln2 |
xd(ln x) = ln3 x + C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∫ |
arcsin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
5) |
|
|
1− x2 |
|
|
|
dx |
= |
∫(arcsin x) 2 d(arcsin x) = 3 |
|
|
(arcsin x) |
|
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Ответ: 1) |
|
sin6 x |
|
+ C ; 2) − |
|
1 |
cos |
9 |
9x + C ; 3) |
arctg8 x |
|
+ C ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
6 |
|
|
|
|
81 |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4) |
|
ln3 x |
+ C ; 5) |
2 |
|
(arcsin x) |
3 |
|
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 11. Найти интегралы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
∫ x(3x − 2) |
24 |
dx ; 2) ∫ x |
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3) ∫ |
|
|
xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1) |
|
|
|
|
|
|
sin(x |
|
+ 1)dx ; |
|
|
|
dx ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
4) |
|
∫ |
|
|
|
dx |
|
|
|
|
|
; 5) |
∫ |
|
|
|
|
|
dx |
|
|
|
|
|
|
; 6) ∫ |
|
|
dx |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x x |
2 |
− a |
2 |
|
|
2ax − x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 2 + 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
∫ x(3x − 2)24 dx = |
|
|
|
|
|
|
dx = 1 dt; x = t + 2 |
|
= 1 |
∫(t + 2)t24 dt = |
1 ∫(t 25 |
+ 2t 24 )dt = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
t = 3x − 2; |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
. |
|||
= |
|
1 |
t |
26 |
|
+ |
|
2t25 |
+ C = |
1 |
(3x |
− 2)26 |
+ |
2(3x − 2)25 |
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
9 |
|
|
|
|
|
|
|
|
|
25 |
|
9 |
|
|
|
|
|
|
26 |
|
|
250 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
∫ x2 sin(x3 + 1)dx = |
|
|
|
|
1 dt; |
|
|
|
|
1 ∫sin tdt = − 1 cost + C = |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
t = x3 + 1; |
|
|
x2 dx = |
|
|
3x2 dx = dt |
= |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
. |
|
|
= − |
1 cos(x3 + 1) + C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
xdx |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
∫ |
dt |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
dx = |
t = x |
|
+ 1; |
|
|
|
|
xdx |
|
= |
2 dt; |
|
|
2xdx = dt |
= |
|
|
t |
= |
2 ln |
|
t |
|
|
+ C = 2 ln |
x |
|
+ 1 |
+ C |
= |
|||||||||||||||||||||||||||||||||||||||||
3) |
|
x2 + 1 |
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||
= |
|
1 ln(x2 + 1) + C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13
