Добавил:

ota Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тольяттинский государственный университет

Предмет:

Высшая математика

Файл:

высшая математика часть 2.pdf

Скачиваний:

115

Добавлен:

26.07.2016

Размер:

505.36 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1111

2.4. Несобственные Интегралы

Пусть функция y = f (x) интегрируема на любом отрезке [a,b] . Тогда, определенный

интеграл ∫ f (x)dx называют еще и собственным интегралом.

В том случае, когда отрезок интегрирования бесконечный или конечный, но подынтегральная функция на этом отрезке терпит разрыв. Второго рода интеграл называется «несобственным» интегралом.

Рассмотрим каждый из двух случаев.

2.4.1. Несобственные интегралы с бесконечными пределами (I рода)

Если функция f (x) определена и непрерывна для всех a ≤ x ≤ +∞ , то по определению

+∞
интеграл ∫ f (x)dx вычисляется по обобщенной формуле Ньютона – Лейбница:
a
+∞
∫ f (x)dx = F(x) a+∞ = F(∞) − F(a)	(2.4.1)

10. Если результат интегрирования конечное число, то интеграл сходится. 20. Если результат интегрирования ∞ - то интеграл расходится.

30. Если результат интегрирования неопределенность, то надо применить определение.

+∞		b			b		b
∫	f (x)dx = lim		f (x)dx ,		∫	f (x)dx = lim		f (x)dx	(2.4.2)
∫		b→+∞ ∫			∫		a→−∞ ∫		(2.4.2)
a		a			−∞		a
	+∞		c			b
	∫	f (x)dx = lim		f (x)dx + lim			f (x)dx		(2.4.3)
	∫		a→−∞ ∫			b→+∞ ∫			(2.4.3)
	−∞		a			c

где с – произвольное число.

Определение: Несобственные интегралы I рода называются сходящимися, если существуют конечные пределы, стоящие в правых частях равенства (2.6). Если же указанные пределы не существуют или бесконечны, то несобственные интегралы называются расходящимися.

Рассмотрим некоторые признаки сходимости и расходимости несобственных интегралов I рода:

10. Признаки сравнения.

Если на промежутке [a,+∞) непрерывные функции			f (x) и ϕ (x) удовлетворяют условию
		+∞		+∞
0 ≤ f (x) ≤ ϕ (x) , то из сходимости интеграла ∫ϕ (x)dx следует сходимость интеграла ∫					f (x)dx , а
		a		a
		+∞	+∞
из расходимости интеграла		∫ f (x)dx следует расходимость интеграла ∫ϕ (x)dx .
		a	a
20. Если при x [a,+∞) ,		f (x) > 0 , ϕ (x) > 0 и существует конечный предел lim		f (x)	= k ≠ 0 ,
20. Если при x [a,+∞) ,		f (x) > 0 , ϕ (x) > 0 и существует конечный предел lim			= k ≠ 0 ,
			x→+∞ ϕ (x)
+∞	+∞
то интегралы ∫ f (x)dx и	∫	ϕ (x)dx сходятся и расходятся одновременно («предельный признак
a	a

сравнения».

+∞			+∞
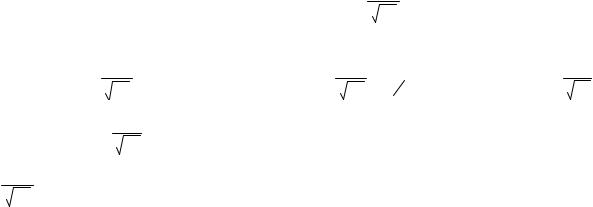
30. Если сходится интеграл ∫	f (x)	dx , то сходится и интеграл	∫ f (x)dx , который в этом
	f (x)	dx , то сходится и интеграл

a			a
		+∞	+∞
случае называется абсолютно – сходящимся. Если же интеграл ∫			f (x)dx сходится, а ∫	f (x)	dx
				f (x)	dx

		a	a

+∞

расходится, то интеграл ∫ f (x)dx называется условно – сходящимся.

Пример 62. Исследовать на сходимость интеграл

+∞ x + 3

∫

3 dx .

Решение:

x + 3

+∞

Здесь

f (x) =

> 0 при x [1,+∞) , при этом

= ϕ (x) , но интеграл ∫1 4

x34

+∞

расходится, т.к.

∫

= 4x 4

= ∞ . Поэтому, согласно признаку сравнения, исходный интеграл

+∞ x + 3

dx расходится.

∫ 4

+∞

Пример 63. Вычислить несобственный интеграл

∫2

xln4 x

Решение:

По определению:

+∞

+∞ d(ln x)

+∞

∫

= ∫

= −

= 0 +

, т.е. интеграл

xln

3ln

(+∞)

3ln

сходится.

Ответ:

+∞

Пример 64. Вычислить интеграл

∫

−∞ x

+ 2x + 5

Решение:

По определению:

+∞

x + 1

+∞

∫

= ∫

+ ∫

arctg

−∞ x

+ 2x + 5

−∞

+ 1)

+ 4

0 (x

+ 1)

−∞

1 arctg 1 −

1 arctg(−∞) +

1 arctg(+∞)

−

1 arctg

= π

Ответ:

π .

Пример 65. Вычислить несобственный интеграл или установить его расходимость

+∞

∫ xsin xdx .

Решение:

По определению:

+∞

u = x du = dx

= lim [− x cos x

∫

xsin xdx =

dv = sin xdx

v = − cos x

+ sin x

+∞

b→+∞

∫udv = u v

0+∞ − ∫vdu

lim [(−bcosb

) + 0 + lim sin b]− sin 0 =

− lim bcosb + lim sin b

b→+∞

+∞

Исходный интеграл

∫

xsin xdx расходящийся, т.к. − lim b cos b , lim sin b не существует.

b→+∞

∞

1− 4sin 2x

dx .

Пример 66. Исследовать сходимость интеграла ∫

Решение:

Функция f (x) = 1− 4sin 2x меняет знак вместе с изменением знака числителя. x3 + 3 x

∞ 1− 4sin 2x

dx . Так как 1− 4sin 2x <

Исследуем сходимость интеграла ∫1

x3 + 3 x

5 , а интеграл

x3 + 3 x

∞

∫

dx = −

сходящийся, то по первому признаку сравнения сходится и интеграл

∞ 1− 4sin 2x

dx также сходится, и притом

∫1

x3 + 3 x

dx . Следовательно, исходный интеграл ∫1

x3 + 3 x

абсолютно.

Пример 67. Исследовать сходимость несобственного интеграла ∫ x cos xdx .

−∞

Решение:

По определению несобственного интеграла I рода:

u = x du = dx

∫

x cos xdx =

dv = cos xdx

v = sin x

= lim (xsin x)

+ cos x

= 0 − lim asin a + 1− lim cos a

a→−∞

−∞

∫udv = u v

0−∞ − ∫sin xdx

−∞

Интеграл расходится, т.к.

lim a sin a , lim cos a не существуют.

a→−∞

2.4.2. Несобственный интегралы от неограниченных функций (II рода)

Если функция y = f (x) определена и непрерывна при a ≤ x ≤ b , интегрируема на любом отрезке [a,b − ε ] , где 0 < ε < b − a , и неограниченна слева от точки b (т.е. f (x) → ∞ при

x → b ) то определенный интеграл вычисляется по формуле:

b		b−ε
∫ f (x)dx =	εlim→+0	∫ f (x)dx	(2.4.4)
a		a

и называется несобственным интегралом от неограниченной функции (II рода).

Если предел в правой части равенства (2.4.4) существует, то несобственный интеграл II рода называется сходящимся; в противном случае – расходящимся.

Аналогично, когда функция f (x) определена и непрерывна при a < x ≤ b , интегрируема на любом отрезке [a + ε ,b] , где0 < ε < b − a и неограниченна справа от точки a (т.е. f (x) → −∞ при x → a ), то определенный интеграл в этом случае вычисляется по формуле (2.8).

b		b
∫ f (x)dx =	εlim→+0	∫ f (x)dx	(2.4.5)
a		a+ε

и также называется несобственным интегралом от неограниченной функции (или II рода). Если функция y = f (x) терпит разрыв II рода во внутренней точке c [a,b] , то

несобственный интеграл II рода определяется формулой (2.4.6).

b	c	b		c−ε		b
∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx =			εlim→+0	∫ f (x)dx +	εlim→+0	∫ f (x)dx	(2.4.6)
a	a	c		a		c+ε

Т.е. представляет собой сумму двух несобственных интегралов II рода. Здесь исходный интеграл вычисляется в предположении, что F(x) первообразная для f (x) . Тогда

b		c−ε		b
∫	f (x)dx = lim	∫	f (x)dx + lim	∫	f (x)dx = lim F(x)	c−ε

	ε →+0		ε →+0		ε →+0	a

a		a		c+ε
= lim F(c − ε ) − F(a) + F(b) − lim F(c + ε )
	ε →+0			ε →+0

+ lim F(x)	b	=

ε →+0	c+ε

В этом случае интеграл называется сходящимся, если только оба несобственных интеграла,

стоящих справа в (2.4.5), сходятся.
Для функций, определенных и положительных на промежутке [a,b)						или (a,b] справедливы
признаки сходимости и расходимости для несобственных интегралов II рода:
1.	Признак сравнения: Пусть функции f (x) и g(x)				определены на [a,b) и интегрируемы
	на каждом отрезке [a,b − ε ] , 0 < ε < b − a и если 0 ≤ f (x) ≤ g(x) , то из сходимости
			b		b	b	b
	интеграла ∫ g(x)dx следует сходимость интеграла ∫ f (x)dx , причем ∫						f (x)dx ≤ ∫ g(x)dx ;
			a		a	a	a
				b			b
	из расходимости интеграла ∫ f (x)dx следует расходимость интеграла ∫ g(x)dx .
				a			a
2. Предельный признак сравнения: Пусть функции					f (x) и g(x) непрерывны на
	промежутке [a,b) и в точке x = b терпят разрыв II рода. Если существует предел
		f (x)		b	b
	lim	f (x)	= k ,	0 < k < +∞ , то интегралы ∫ f (x)dx и ∫ g(x)dx сходятся и расходятся
	lim		= k ,
	x→+∞ g(x)			a	a
	одновременно.
3.	Если функция			f (x) знакопеременная на отрезке [a,b] и имеет разрыв в точке x = b , и

b		b
несобственный интеграл ∫	f (x)	dx сходится, то сходится и интеграл ∫ f (x)dx . В этом


a		a
b		b

случае интеграл ∫ f (x)dx называется абсолютно сходящимся. Если же интеграл ∫ f (x)dx

a a

сходится, а интеграл ∫

f (x)

dx расходится, то интеграл ∫ f (x)dx называется условно

сходящимся. Указанные признаки справедливы и для несобственных интегралов

∫ f (x)dx , где

f (x) неограниченна справа от точки a .

Замечание: В качестве эталона для сравнения функций часто берут функцию ϕ (x) =

(b − x)

Можно показать, что несобственный интеграл ∫a

(α > 0)

сходится при α < 1 и

(b − x)α

расходится при α ≥ 1 (2.10). это же относится и к интегралу ∫a

(x − a)α

3 dx .

Пример 68. Вычислить несобственный интеграл (или доказать его расходимость) ∫

ln x

Решение:

Подынтегральная функция f (x) =

неограниченна в окрестности точки x = 1. На

любом же отрезке [ε + 1,e]

ln x

она интегрируема, т.к. является непрерывной функцией. Поэтому:

3 3

∫

= εlim→+0 ∫

−

ln x

= εlim→+0

εlim→+0

(1+ ε )

1+ε

Интеграл сходится.

Ответ:

Пример 69. Вычислить несобственный интеграл (или доказать его расходимость)

Решение:

Подынтегральная функция f (x) = cos1 x неограниченна в окрестности точки x = π2

интегрируема на любом отрезке [0, π2 − ε ] как непрерывная функция. Поэтому:

−ε

= lim

= lim ln tg

−

= ∞ .

∫

cos x

∫

cos x

ε →+0

Следовательно, интеграл – расходится.

1 dx

Пример 70. Вычислить несобственный интеграл ∫0 1− x3 .

2 dx

∫0 cos x .

Решение:

Подынтегральную функцию f (x) = 1−1x3 представим в виде суммы простых дробей:

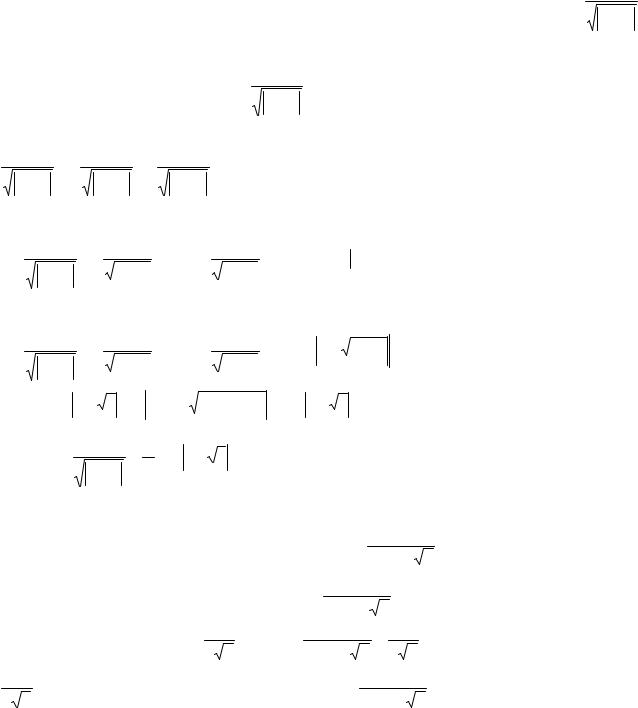
f (x) =		1		=	1			=	1		1	+		x + 2
																.
	1	− x	3		(1− x)(1+ x + x	2	)		3		− x		1+ x + x		2	.
	1	− x			(1− x)(1+ x + x		)		3	1	− x		1+ x + x

x + 2

Тогда:

∫0

1− x3

1− x

1+ x + x2

1−ε

= − lim ln(1− x)

т.к. ∫

= lim

∫

10−ε

= ∞ .

1− x

ε →+0

Второй интеграл вычислять нет уже надобности, т.к. этот интеграл собственный, а исходный интеграл уже расходится.

∫

Пример 71. Вычислить несобственный интеграл (или доказать его расходимость)

1− x2

Решение:

f (x) =

1− x2

Подынтегральная функция

неограниченна в окрестности точки x = 1,

являющейся внутренней точкой промежутка интегрирования. Поэтому, по определению:

∫

= ∫

+ ∫

1− x2

, где:

При 0 ≤ x ≤ 1:

1−ε

[arcsin(1− ε ) − 0] = π

∫

= ∫

= lim

∫

= lim arcsinx10−ε

= lim

1− x2

ε →+0

1− x2

ε →+0

;

При 1 ≤ x ≤ 2 :

∫

= ∫

= lim

∫

= lim ln x + x2 −1

1+ε

1− x2

1− x

ε →+0

1+ε

1− x

ε →+0

= lim

ln 2 +

3 − ln1+ ε +

(1+ ε )2 −1 = ln 2 +

ε →+0

∫

+ ln 2 +

Ответ: 0

1− x

Пример 72. Исследовать на сходимость интеграл ∫

+ 2

Решение: Подынтегральная функция f (x) = 3x2 + 23 x терпит разрыв II рода в точке x = 0 .

Сравним ее с функцией

ϕ (x) =

. Так как

3x2

, а несобственный интеграл

+ 23 x 23

dx3

dx 3

∫

сходится, следовательно исходный интеграл ∫

сходится по признаку

2 x

0 3x

+ 2

сравнения.

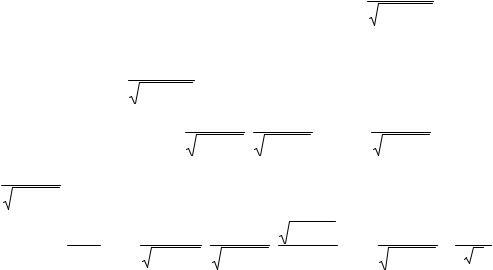
															1		cos	2	x2	2 dx .
		Пример 73. Исследовать на сходимость интеграл ∫															cos		x2	2 dx .
															0	3 (1− x )
		Решение:
		Функция f (x) =				cos2 x			терпит бесконечный разрыв (II рода) в точке x = 1. Перепишем
					3	(1− x2 )2
эту функцию в виде:						f (x) =		cos2 x						1	. ϕ (x) =		1				; интеграл
							3 (1+ x)2				3 (1			− x)2		3 (1− x)2
1		1		1	−	2						1	1
1		1		1	−	2						1	1
∫			2	= −∫(1− x)		3	d(1− x)				3			= 3 - сходится.
∫	3	(1− x)	2	= −∫(1− x)			d(1− x)		= −3(1− x)					= 3 - сходится.
0	3			0									0
0				0									0
		Т.к. lim		f (x)	= lim		cos2 x			1				3 (1− x)2			cos2 x				=	cos2	1	(≠ 0,	≠ ∞) , то
		Т.к. lim		ϕ (x)	= lim									1	= lim			+ x)2			=	3 4		(≠ 0,	≠ ∞) , то
		x→1		ϕ (x)	x→1 3 (1+ x)2				3 (1	− x)2				1	x→1 3 (1			+ x)2				3 4

согласно предельному признаку сравнения, исходный интеграл также сходится.

2.5.Тесты (теория)

1.Дайте определение несобственного интеграла I рода.

2.Дайте определение несобственного интеграла II рода.

3.Дайте определение признака сравнения для несобственных интегралов I рода.

4.Дайте определение частного признака сравнения для несобственных интегралов.

5.Дайте определение признака абсолютной сходимости несобственных интегралов.

6.Покажите, как производится вычисление несобственных интегралов с неограниченными пределами.

7.Покажите, как производится вычисление несобственных интегралов от неограниченных функций.

8.Покажите, как производится вычисление несобственных интегралов от функций f (x) в окрестности точки c , где a < c < b , а f (c) → ±∞ .

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1111

Соседние файлы в предмете Высшая математика

#
26.07.2016178.67 Кб20высшая математика структура дисциплины часть 3.pdf
#
26.07.2016113.73 Кб23высшая математика структура дисциплины часть 4.pdf
#
26.07.20161.43 Mб111высшая математика теоретический материал часть 3.pdf
#
26.07.2016158.98 Кб36высшая математика установочные лекции часть 3.pdf
#
26.07.201691.65 Кб14высшая математика характеристика дисциплины.pdf
#
26.07.2016505.36 Кб115высшая математика часть 2.pdf
#
26.07.2016500.27 Кб210математика и информатика курс лекций.pdf
#
26.07.20161.17 Mб273математика и информатика метод указания.pdf
#
26.07.2016483.87 Кб42математика индивид дом задания .pdf
#
26.07.2016721.05 Кб108метод указания по решению задач.pdf
#
26.07.2016547.48 Кб32методы анализа нелиненых цепей.pdf