13. Обработка прямых многократных измерений.

1. Из результатов наблюдений исключают известные систематические погрешности.

2. Если есть подозрение о наличии грубых погрешностей, то проверяют гипотезу по критерию t_Г. Для этого находят значение среднего арифметического А_ср, исключив из него систематическую погрешность, значение среднего квадратического отклонения σ^*_Δ, а далее вычисляют t_Г1=(A_cp-A_nmin)/σ^*_v ; t_Г2=(A_nmax-A_cp)/σ^*_v

Значения t_Г1 и t_Г2 сравнивают с табличным t_Г. Если t_Г1 и t_Г2 больше t_Г, то A_nmin и A_nmax исключают из дальнейшей обработки.

3. Вычисляют А_ср, σ^*_v σ^*_Acp исправленных результатов наблюдений.

σ^*_Acp = σ^*_v/√n’ .4. Если распределение подчин-ся нормальному з-ну, то задаётся довер вер-тью α и по ней находят β, Δ_α или t_c, Δ_α Δ_α=2β· σ^*_Acp где β - табличная величина, значение аргумента интеграла вероятности Ф(β);

5. определяют границы неисключенной систематической погрешности Q – погрешности обусловленные классом точности прибора. Для абсолютной погрешности Q=Δ=A₀-A_n=±α. Для относительной погрешности Q=±(δ/100)·A_cp Для привидённых Q = (γ/100)A_cp

Если имеется несколько неучтённых погрешностей необходимо найти:

где m – число погрешностей;

К = 1,1 при доверительной вероятности α=0.95.

6. Определяют отношение Q_Σ/σ^*_Acp. Если оно меньше 0,8, то неисключенными погрешностями пренебрегают.

Если оно больше 8, то пренебрегают случайной погрешностью и считают, что Δ=2θ_Σ.

Если 0,8 < θ_Σ/σ^*_Acp < 8, то при определении границ погрешности нужно учитывать и случайную и систематическую составляющие. Δ_Σ=K’·σ_Σ, где ,.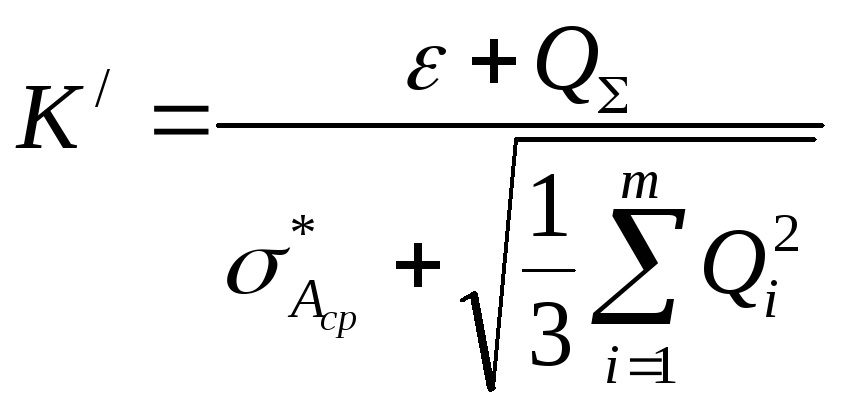

Результат измерения и погрешности представляют в виде A₀=(A_cp±Δ_Σ); α.

14. Обработка результатов нескольких групп измерений.

В практике измерений часто встречаются ситуации, когда необходимо найти наиболее достоверное значение величины на основании измерений, выполненных разными операторами, различными измерительными приборами и в различных условиях. Представляемые каждым оператором оценки называют, в таких ситуациях, рядами. Очевидно, что они неравноточные. Обработка таких неравноточных результатов направлена на получение наиболее достоверного значения измеряемой величины А_р.

Пусть истинное значение измеряемой величины равно А₀. Пусть также, в результате m неравноточных измерений получены ряды A_cp1,σ^*_v1; A_cp2,σ^*_v2; … ; A_cpm,σ^*_vm Тогда вероятнейшее значение А_р может быть найдено по формуле:

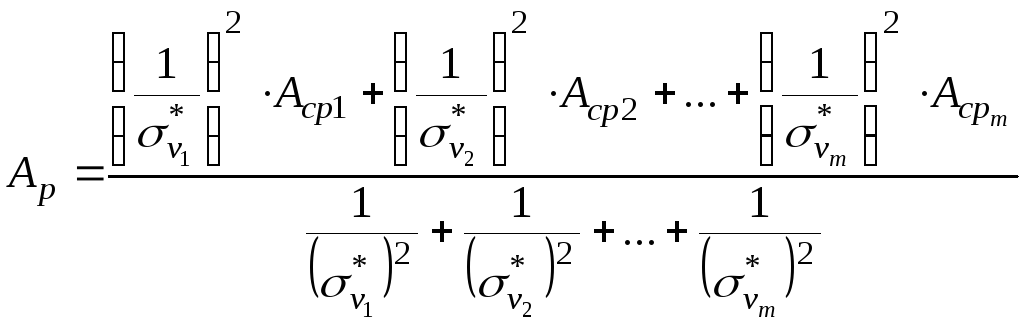(5.3)

Формула (5.3) неудобна для практического применения, так как обычно значение σ^*_vi сильно отличаются от единицы. Поэтому её преобразуют.

Введем некоторый коэффициент μ², на который умножим числитель и знаменатель правой части (5.3). Величину μ² выбирают так, чтобы отношение (μ/σ^*_vi)² было возможно ближе к единице. Величину (μ/σ^*_vi)² называют весом и обозначают p_i. С учетом этого формула (5.4) примет вид:

Величину А_р, полученную по (5.5), называют весовым средним или общей арифметической срединой. Оценку абсолютного значения среднеквадратического отклонения погрешности определяют выражением, аналогичным

Д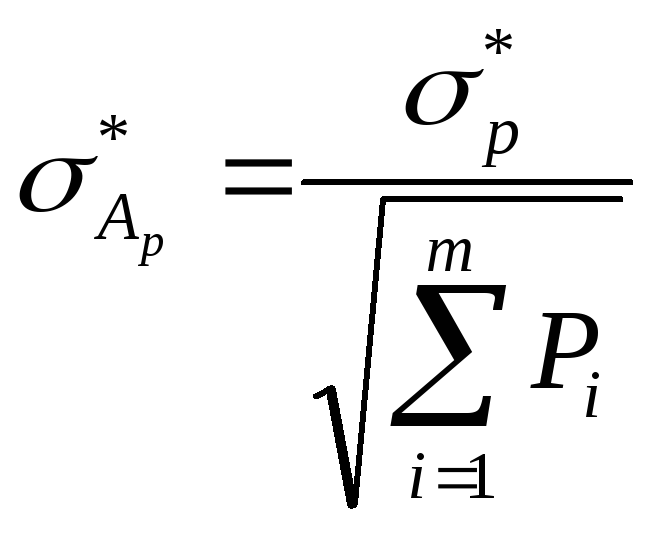ля оценки остаточной погрешности (погрешности весового среднего), пользуются формулой

Если значения σ^*_vi отсутствуют, но известно число измерений, выполненных в каждом неравноточном ряде п_i, то полагают п_{i ≈} σ^*_vi