Электротехника+лекции

Мгновенные значения – значения изменяющихся во времени э.д.с, тока,

напряжения, мощности в любой момент времени. На протяжении одного периода можно взять бесчисленное множество мгновенных значений.

Мгновенные значения обозначаются строчными буквами: е,i,u, р.

Амплитудное значение – наибольшее мгновенное значение синусоидальной э.д.с. тока, напряжения, мощности, обозначается прописной

буквой с индексом т (max): Em, Im, Um, Pm.

Рассмотрим получение синусоиды путем вращения вектора (рис. 2.3).

Допустим, что вектор ОА соответствует максимальному значению Ет

синусоидальной функции e = Em sin ωt и вращается против часовой стрелки с угловой скоростью ω, а угол α = ωt непрерывно изменяется. Проекция вектора

ОА на вертикальную ось равна: e = OA·sinα = OA·sinωt = Em sin ωt.

Аргумент синуса, т.е. величина ωt (может быть ωt + ψ ) называется фазой,

промышленной частоты f = 50 Гц, ω = 2·3,14·50=314 (1/с).

Если две синусоидально изменяющиеся величины проходят в одно и то же время через нулевые и максимальные значения, то эти две величины совпадают по фазе (рис. 2.4).

Рис. 2.4. Синусоидальные величины, совпадающие по фазе

Если e = Em sin (ωt – ψ1), а I = Im sin (ωt – ψ2 ), то эти две величины не будут совпадать по фазе (рис. 2.5). Угол ψ1 – ψ2 = φ называется углом сдвига по фазе.

Рис. 2.5. Синусоидальные величины, несовпадающие по фазе

2.3. Действующее значение синусоидального тока

Действующее значение синусоидального тока определяется по формуле:

I 1 T i2dt

T 0 .

При i = Im sin ωt получаем

так как

Аналогично действующие значения э.д.с. и напряжений равны соответственно

E Em 0,707 Em 2

U Um 0,707 Um 2

2.4. Среднее значение синусоидального тока

Под средним значением синусоидально изменяющейся величины понимают среднее значение ее за полпериода:

Аналогично средние значения э.д.с. и напряжений равны соответственно

2.5. Цепь переменного тока с активным сопротивлением

Резистор R включен на синусоидальное напряжение U=Umsinωt (рис. 2.6),

под действием напряжения по цепи протекает ток i. Величина сопротивления R

Рис. 2.6. Цепь переменного тока с активной нагрузкой

С увеличением частоты это отношение также увеличивается за счет поверхностного эффекта (скин-эффекта), эффекта вытеснения тока на поверхность проводника. Э.д.с. самоиндукции в проводниках переменного

где: L – индуктивность проводника;

dtdi – изменение тока во времени, поэтому плотность тока по сечению проводника неодинакова.

На переменном токе сопротивление резистора R называют активным, а на постоянном – омическим.

По закону Ома мгновенное значение тока в цепи (см. рис. 2.6):

i U Um sin t Im sin t , R R

т.е. напряжение и ток совпадают по фазе, а угол сдвига фаз равен нулю: φ=0.

На рис. 2.7 представлены графики изменения напряжения и тока в данной цепи и ее векторная диаграмма.

Рис. 2.7. Графики изменения напряжения и тока в цепи с активным сопротивлением (а); векторная диаграмма цепи (б)

Диаграмма, изображающая совокупность векторов, построенных с соблюдением их взаимной ориентации по фазе, называется векторной диаграммой.

2.6. Цепь переменного тока с идеальной катушкой индуктивности

Катушка индуктивности L включена в цепь синусоидального тока i = =Imsinωt (рис. 2.8). Катушка, у которой активное сопротивление R = 0

называется идеальной. Согласно второму закону Кирхгофа напряжение на входе цепи:

U e L di L Im sin t LIm cos t LIm sin(t 90 ) Um sin(t 90 ) , dt dt

т.е. напряжение опережает ток на 90°, или ток отстает от напряжения на 90°,

следовательно, индуктивность создает сдвиг по фазе.

Рис. 2.8. Цепь переменного тока с индуктивной нагрузкой

Произведение ωL = 2πfL – индуктивное сопротивление, которое зависит от частоты питающего напряжения f и индуктивности L.

На рис. 2.9 представлены графики изменения напряжения и тока в катушке индуктивности, векторная диаграмма цепи.

Рис. 2.9. Графики изменения напряжения и тока в цепи с идеальной катушкой индуктивности (а); векторная диаграмма цепи (б)

2.7. Цепь переменного тока с идеальным конденсатором

Конденсатор С включен в цепь с напряжением U = Umsinωt (рис. 2.10).

Конденсатор, у которого активное сопротивление R = 0, называется идеальным.

Рис. 2.10. Цепь переменного тока с емкостной нагрузкой

Если напряжение на конденсаторе изменяется по синусоидальному закону, то по синусоидальному закону изменяется и заряд конденсатора:

q = C·U = CUmsinωt.

Ток, протекающий через конденсатор:

т.е. ток через конденсатор опережает по фазе напряжение на угол 90°.

которое обратно пропорционально частоте питающего напряжения и емкости конденсатора.

На рис. 2.11 представлены графики изменения напряжения и тока в конденсаторе, векторная диаграмма цепи.

а б

Рис. 2.11. Графики изменения напряжения и тока в цепи с идеальным конденсатором (а); векторная диаграмма цепи (б)

2.8. Цепь переменного тока с катушкой индуктивности

Под действием напряжения u по катушке протекает ток i = Imsinωt (рис. 2.12). Приложенное напряжение u является суммой двух составляющих – активной u R и реактивной (индуктивной) uL :

u = u R + u L = Umsinωt + Umsin (ωt + 90º).

Рис. 2.12. Цепь переменного тока с активно-индуктивной нагрузкой

Активная составляющая uR = i·R совпадает по фазе с током, а индуктивная u L = i·XL опережает по фазе ток на четверть периода.

Векторную диаграмму для этой цепи обычно начинают строить с вектора тока Ī так как при последовательном соединении элементов ток на всех участках цепи одинаков (рис. 2.13, а). Далее откладываем вектор ŪR который совпадает по фазе с вектором тока Ī. Под углом 90° к вектору Ī откладываем вектор напряжения ŪL. Результирующий вектор Ū = ŪR + ŪL. Из треугольника напряжений определяем действующее значение приложенного напряжения:

U 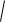UR2 UL2 .

Треугольнику напряжений подобен треугольник сопротивлений (рис.2.13,

Рис. 2.13. Векторная диаграмма цепи с последовательным соединением R, L (а); треугольник сопротивлений (б)

2.9. Цепь переменного тока с конденсатором

Если по цепи (рис. 2.14) протекает ток i = Imsinωt, то подводимое напряжение u равно сумме напряжений на активном сопротивлении и конденсаторе:

u = uR + uC = Umsinωt + Umsin(ωt – 90º).

Рис. 2.14. Цепь переменного тока с активно-емкостной нагрузкой

Активная составляющая напряжения совпадает по фазе с током, а емкостная составляющая отстает на четверть периода. Действующее значение подводимого к цепи напряжения

Векторная диаграмма строится аналогично предыдущему случаю (рис.

2.15). За исходный вектор принимаем вектор тока Ī. Вектор ŪR совпадает по фазе с вектором Ī. Под углом 90° откладываем вектор ŪC. Вектор приложенного напряжения к цепи Ū = ŪR + Ūс.

Рис. 2.15. Векторная диаграмма цепи с последовательным соединением R, C (а); треугольник сопротивлений (б)

2.10. Комплексный метод расчета цепей переменного тока

Тригонометрическая форма расчета электрических цепей практически применима только для простейших цепей, не содержащих большого числа контуров и источников, поэтому широкое применение получил алгебраический метод, позволяющий рассчитывать цепи переменного тока аналогично цепям постоянного тока – комплексный метод (метод комплексных амплитуд, или символический метод).

Комплексное число, соответствующее точке, в которой лежит конец вектора (рис. 2.16), может быть записано в следующих формах: алгебраической

А = a1 + ja2; тригонометрической А = a(cosα + jsinα); показательной А = a·ejα и

полярной (угловой) А = a·∟α,

где: a1 = a·cosα = Re[ А ] – действительная (вещественная) часть комплексного

числа А ;

a2 = a·sinα = Im[ А ] – мнимая часть комплексного числа А ;