
- •Ряды фурье
- •§1. Ортонормированные системы и общие ряды фурье
- •§2. Замкнутые и полные ортонормированные системы
- •§3. Замкнутость тригонометрической системы и следствия из нее
- •3. Следствия замкнутости тригонометрической системы.
- •§4. Простейшие условия равномерной сходимости и почленного дифференцирования тригонометрического ряда фурье
- •2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье.
- •§5. Более точные условия равномерной сходимости и условия сходимости в данной точке
- •3. Вспомогательные предложения.
- •§ 6. Кратные тригонометрические ряды фурье
- •Глава 9 преобразование фурье
- •§ 1. Представление функции интегралом фурье
- •2. Основная теорема. Формула обращения.
- •§ 2. Некоторые свойства преобразования фурье
- •§ 3. Кратный интеграл фурье
3. Вспомогательные предложения.
Лемма.
Пусть
![]() кусочно
непрерывная на сегменте
кусочно
непрерывная на сегменте
![]() и периодически с периодом
и периодически с периодом![]() продолжена на всю бесконечную прямую.
Тогда для любого
продолжена на всю бесконечную прямую.
Тогда для любого![]() найдется
такое
найдется
такое![]() ,
что при всех
,
что при всех![]() ,
удовлетворяющих условию
,
удовлетворяющих условию![]() ,
справедливо неравенство
,
справедливо неравенство
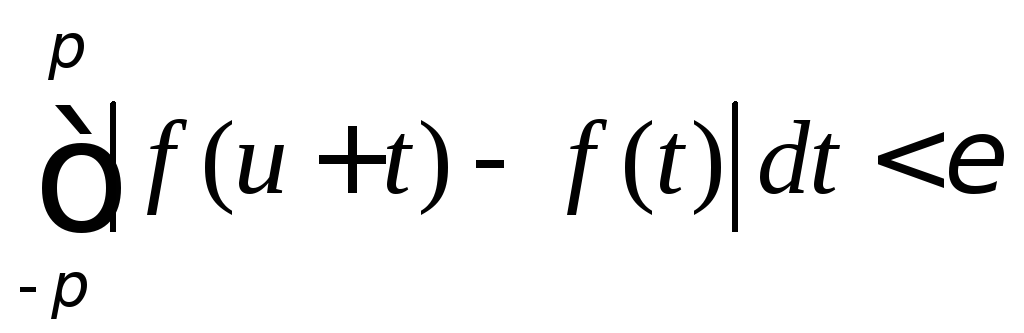 .
.
Доказательство.
Фиксируем произвольное
![]() .
Согласно теореме 8.8 (о замкнутости
тригонометрической системы) для функции
.
Согласно теореме 8.8 (о замкнутости
тригонометрической системы) для функции
![]() найдется
тригонометрический многочлен
найдется
тригонометрический многочлен
![]() такой, что
такой, что
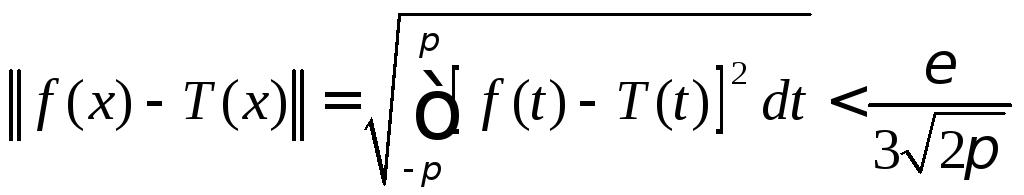 ,
,
и потому на основании неравенства Коши-Буняковского20
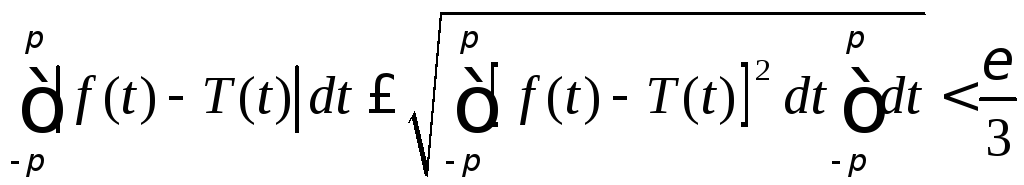 .
(8.56)
.
(8.56)
Из
неравенства (8.56), из леммы п. 2 и из того,
что
![]() и
и
![]() являются
периодическими функциями периода
являются
периодическими функциями периода
![]() ,
заключаем, что для любого числа
,
заключаем, что для любого числа
![]()
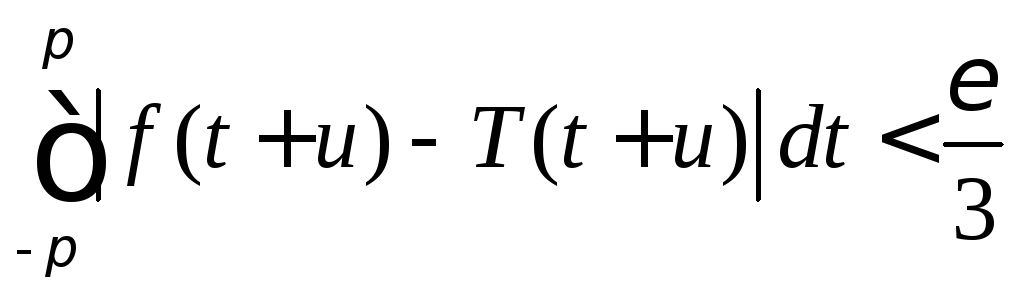 .
(8.57)
.
(8.57)
Поскольку
модуль суммы трех величин не превосходит
сумму модулей этих величин, то для любого
числа
![]() справедливо неравенство
справедливо неравенство
 .
(8.58)
.
(8.58)
Теперь
остается заметить, что в силу непрерывности
тригонометрического многочлена и
теоремы Кантора (см. теорему 4.16 ч.1) для
фиксированного нами
![]() найдется
найдется![]() такое,
что при
такое,
что при
![]() и
и
![]() при всех из
при всех из
![]()
![]()
и потому
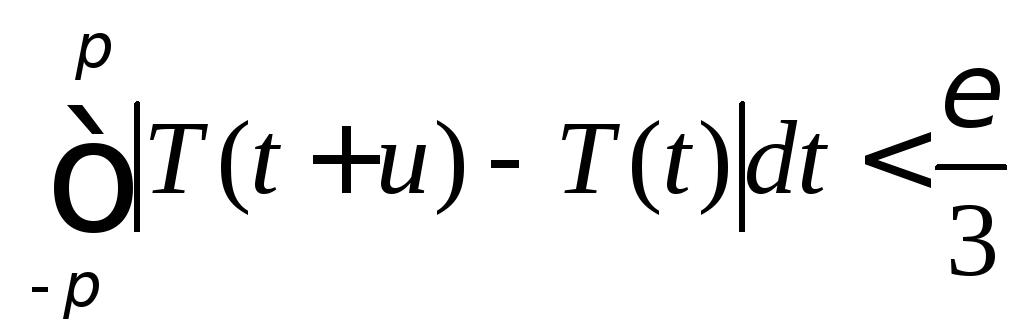 .
(8.59)
.
(8.59)
Сопоставляя неравенство (8.58) с неравенствами (8.56), (8.57) и (8.59), получим
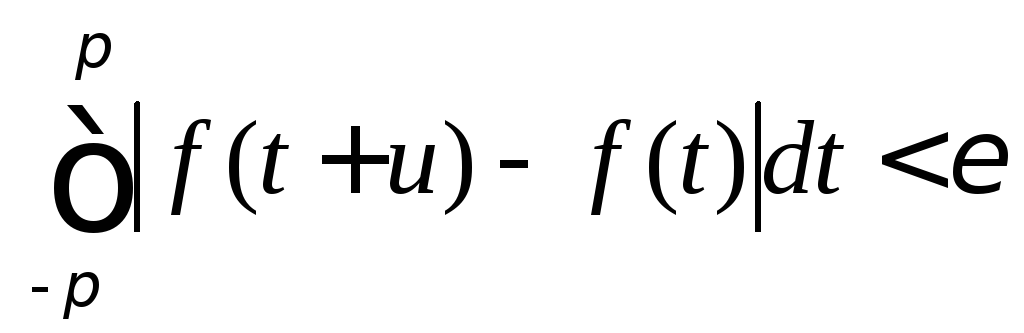 (8.60)
(8.60)
для
всех
![]() ,
для которых
,
для которых
![]() .
Лемма доказана.
.
Лемма доказана.
Извлечем теперь из этой леммы ряд важных для дальнейшего следствий.
Следствие
1. Если функция![]() кусочно непрерывна на сегменте
кусочно непрерывна на сегменте![]() и периодически (с периодом
и периодически (с периодом![]() )
продолжена на всю бесконечную прямую,
а
)
продолжена на всю бесконечную прямую,
а
![]() - любая фиксированная точка сегмента
- любая фиксированная точка сегмента
![]() ,
то для любого
,
то для любого![]() найдется
найдется
![]() такое,
что
такое,
что
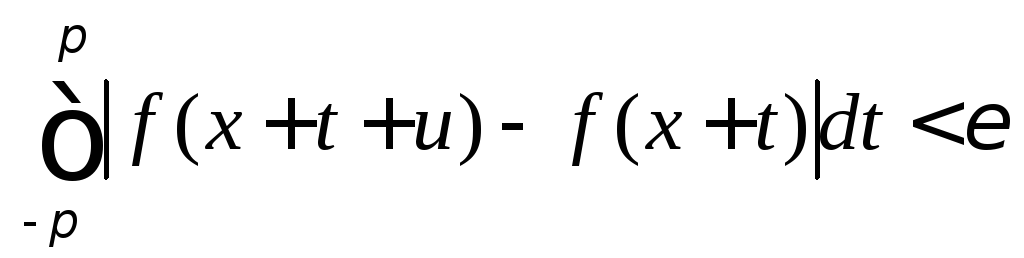 (8.61)
(8.61)
при
![]() .
.
Доказательство.
Сделаем в интеграле, стоящем в левой
части (8.61), замену переменной![]() :
:
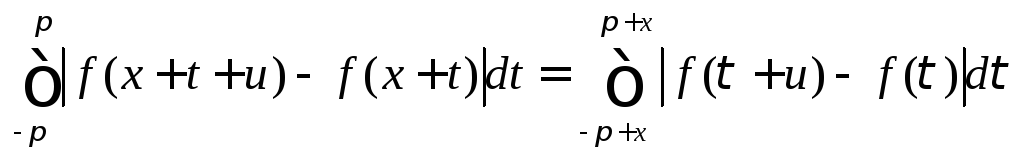 .
.
В силу равенства (8.49)
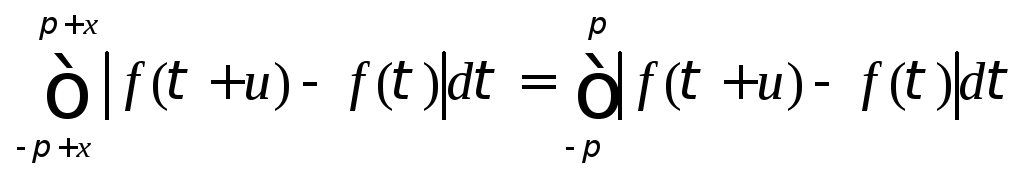 .
.
Следовательно, неравенство (8.61) является следствием (8.60).
Следствие
2. Если каждая из функций
![]() и
и
![]() кусочно
непрерывна на сегменте
кусочно
непрерывна на сегменте![]() и
периодически (с периодом
и
периодически (с периодом![]() )
продолжена на всю прямую, то функция
)
продолжена на всю прямую, то функция
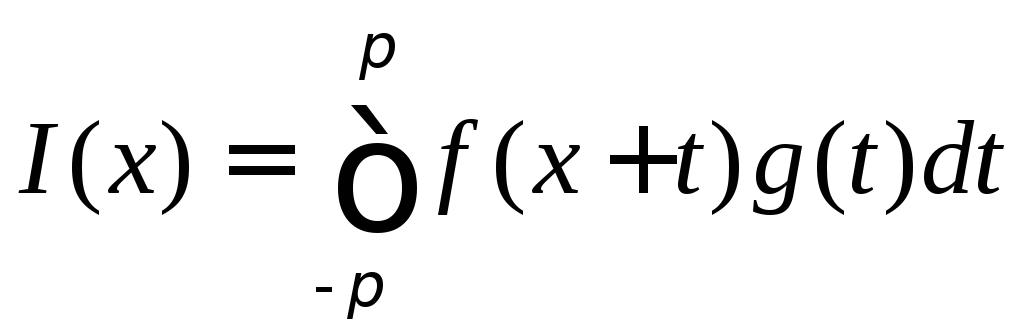
является
непрерывной функцией
![]() на
сегменте
на
сегменте
![]() .
.
Доказательство.
Пусть
![]() - любая точка сегмента
- любая точка сегмента
![]() .
Тогда
.
Тогда
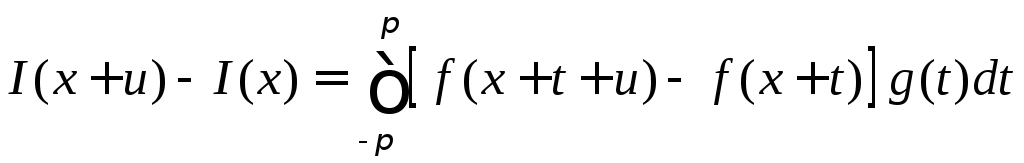 ,
,
и
поскольку кусочно непрерывная на
сегменте
![]() функция
функция
![]() удовлетворяет
на этом сегменте условию ограниченности
удовлетворяет
на этом сегменте условию ограниченности
![]() ,
то
,
то
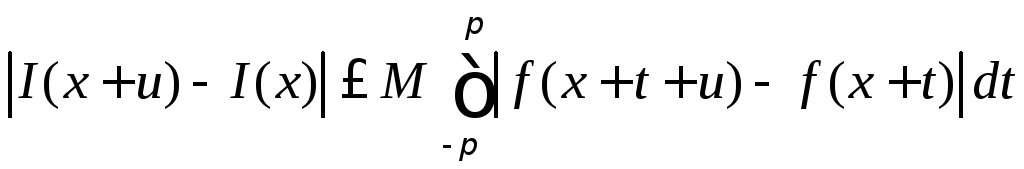 ,
,
и
потому в силу (8.61) для любого
![]()
![]() при
при
![]() .
.
Непрерывность
![]() в точке
в точке![]() доказана.
доказана.
Следствие
3.
Если
каждая из функций
![]() и
и
![]() кусочно
непрерывна на сегменте
кусочно
непрерывна на сегменте![]() и
периодически (с периодом
и
периодически (с периодом
![]() )
продолжена на всю прямую, то
тригонометрические коэффициенты Фурье
функции
)
продолжена на всю прямую, то
тригонометрические коэффициенты Фурье
функции
![]() при разложении ее по переменной
при разложении ее по переменной
![]()
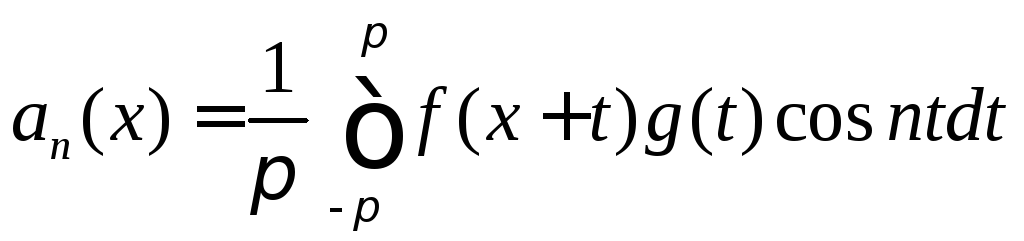 ,
(8.62)
,
(8.62)
 (8.63)
(8.63)
при
![]() сходятся к нулю равномерно относительно
сходятся к нулю равномерно относительно![]() на сегменте
на сегменте![]() (а, следовательно, и на всей прямой).
(а, следовательно, и на всей прямой).
Доказательство.
Для любой фиксированной точки
![]() сегмента
сегмента
![]() функция
функция![]() является кусочно непрерывной функцией
аргумента
является кусочно непрерывной функцией
аргумента![]() на сегменте
на сегменте
![]() ,
поэтому для нее справедливо равенство
Парсеваля21
,
поэтому для нее справедливо равенство
Парсеваля21
 .
(8.64)
.
(8.64)
Из
равенства (8.64) вытекает сходимость ряда,
стоящего в левой его части, в каждой
фиксированной точке
![]() сегмента
сегмента
![]() .
Так как указанный ряд состоит из
неотрицательных
членов, то в силу теоремы Дини22
для доказательства равномерной на
сегменте
.
Так как указанный ряд состоит из
неотрицательных
членов, то в силу теоремы Дини22
для доказательства равномерной на
сегменте
![]() сходимости
указанного ряда достаточно доказать,
что как функции
сходимости
указанного ряда достаточно доказать,
что как функции
![]() и
и![]() ,
так и сумма ряда (8.64)
,
так и сумма ряда (8.64)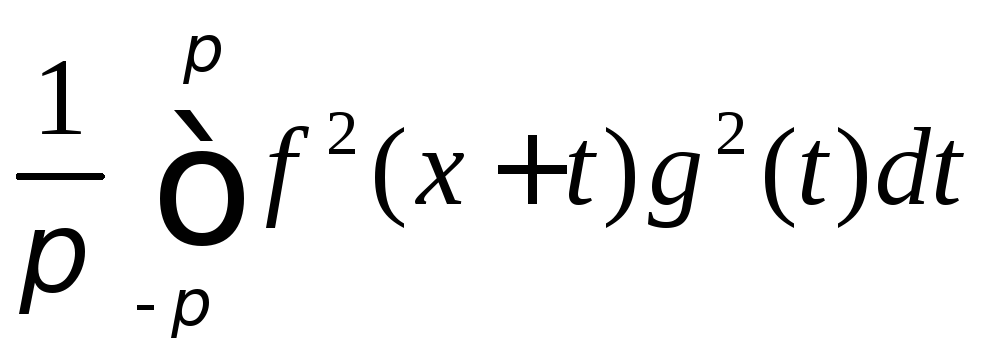 -
непрерывная функция
-
непрерывная функция
![]() на
сегменте
на
сегменте
![]() ,
а это сразу вытекает из предыдущего
следствия (достаточно учесть, что квадрат
кусочно непрерывной функции является
кусочно непрерывной функцией и что
,
а это сразу вытекает из предыдущего
следствия (достаточно учесть, что квадрат
кусочно непрерывной функции является
кусочно непрерывной функцией и что
![]() и
и![]() при каждом фиксированном номереn
являются непрерывными функциями).
при каждом фиксированном номереn
являются непрерывными функциями).
Следствие
4. Если каждая из функций
![]() и
и
![]() кусочно
непрерывна на сегменте
кусочно
непрерывна на сегменте
![]() и
периодически с периодом
и
периодически с периодом
![]() продолжена на всю прямую, то
последовательность
продолжена на всю прямую, то
последовательность
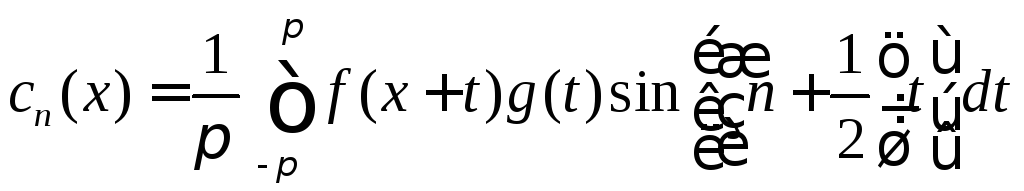 (8.65)
(8.65)
сходится
к нулю равномерно относительно
![]() на сегменте
на сегменте![]() (а следовательно, и на всей прямой).
(а следовательно, и на всей прямой).
Доказательство. Достаточно учесть, что
![]()
и
применить предыдущее следствие, беря
в (8.62) вместо
![]() функцию
функцию![]() ,
а в (8.63) вместо
,
а в (8.63) вместо![]() функцию
функцию![]() .
.
4.
Принцип локализации.
В этом пункте мы докажем, что вопрос о
том, сходится или расходится
тригонометрический ряд Фурье кусочно
непрерывной на сегменте
![]() и
периодической (с периодом
и
периодической (с периодом
![]() )
функции
)
функции
![]() в данной точке
в данной точке
![]() ,
решается лишь на основании поведения
функции
,
решается лишь на основании поведения
функции
![]() в как угодно малой окрестности точки
в как угодно малой окрестности точки
![]() .
Это замечательное свойство
тригонометрического ряда Фурье принято
называть принципом
локализации.
.
Это замечательное свойство
тригонометрического ряда Фурье принято
называть принципом
локализации.
Начнем с доказательства важной леммы.
Лемма
(лемма Римана). Если функция
![]() кусочно
непрерывна на сегменте
кусочно
непрерывна на сегменте![]() и периодически (с периодом
и периодически (с периодом
![]() )
продолжена на всю прямую и если эта
функция обращается в нуль на некотором
сегменте
)
продолжена на всю прямую и если эта
функция обращается в нуль на некотором
сегменте
![]() 23,
то для любого положительного числа
23,
то для любого положительного числа
![]() ,
меньшего
,
меньшего
![]() ,
тригонометрический ряд Фурье функции
,
тригонометрический ряд Фурье функции
![]() равномерно
на сегменте
равномерно
на сегменте
![]() сходится к нулю.
сходится к нулю.
Доказательство.
Пусть
![]() - произвольное положительное число,
меньшее
- произвольное положительное число,
меньшее![]() .
Частичная сумма тригонометрического
ряда Фурье функции
.
Частичная сумма тригонометрического
ряда Фурье функции![]() в
произвольной точке
в
произвольной точке
![]() числовой
прямой определяется равенством (8.54).
Полагая
числовой
прямой определяется равенством (8.54).
Полагая
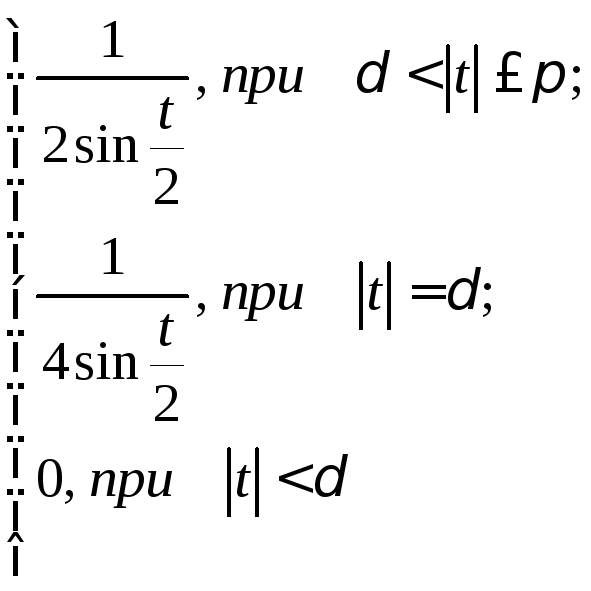 (8.65)
(8.65)
и
учитывая, что
![]() равняется нулю при условии, что
равняется нулю при условии, что![]() принадлежит
сегменту
принадлежит
сегменту
![]() ,
а
,
а![]() принадлежит
сегменту
принадлежит
сегменту![]() 24,
можно следующим образом переписать
равенство (8.54) для каждой точки
24,
можно следующим образом переписать
равенство (8.54) для каждой точки
![]() сегмента
сегмента![]() :
:
 .
.
Остается принять во внимание, что последовательность, стоящая в правой части последнего равенства, в силу следствия 4 п. 3 сходится к нулю равномерно
относительно![]() на всей числовой прямой. Лемма доказана.
на всей числовой прямой. Лемма доказана.
Непосредственными следствиями доказанной леммы являются следующие две теоремы.
Теорема
8.11. Пусть функция
![]() кусочно
непрерывна на сегменте
кусочно
непрерывна на сегменте![]() и периодически (с периодом
и периодически (с периодом![]() )
продолжена на всю прямую, и пусть
)
продолжена на всю прямую, и пусть
![]() - некоторый сегмент. Для того, чтобы
тригонометрический ряд Фурье функции
- некоторый сегмент. Для того, чтобы
тригонометрический ряд Фурье функции
![]() при любом положительном
при любом положительном![]() , меньшем
, меньшем
![]() , сходился (к этой функции) равномерно
на сегменте
, сходился (к этой функции) равномерно
на сегменте
![]() ,
достаточно чтобы существовала кусочно
непрерывная на сегменте
,
достаточно чтобы существовала кусочно
непрерывная на сегменте![]() и периодическая (с периодом
и периодическая (с периодом![]() )функция
)функция
![]() ,
обладающая равномерно сходящимся на
сегменте
,
обладающая равномерно сходящимся на
сегменте![]() тригонометрическим рядом Фурье и
совпадающая на сегменте
тригонометрическим рядом Фурье и
совпадающая на сегменте
![]() с
функцией
с
функцией![]() .
.
Доказательство.
Применяя лемму Римана к разности
![]() ,
получим, что тригонометрический ряд
Фурье разности
,
получим, что тригонометрический ряд
Фурье разности![]() при любом
при любом![]() из интервала
из интервала![]() сходится
к нулю равномерно на сегменте
сходится
к нулю равномерно на сегменте![]() ,
а отсюда и из равномерной на сегменте
,
а отсюда и из равномерной на сегменте![]() сходимости тригонометрического ряда
Фурье функции
сходимости тригонометрического ряда
Фурье функции![]() вытекает
равномерная на сегменте
вытекает
равномерная на сегменте![]() сходимость тригонометрического ряда
Фурье функции
сходимость тригонометрического ряда
Фурье функции![]() .
Тот факт, что последний ряд сходится на
сегменте
.
Тот факт, что последний ряд сходится на
сегменте![]() именно
к функции
именно
к функции
![]() ,
непосредственно вытекает из следствия
5 п. 3 § 3. Теорема доказана.
,
непосредственно вытекает из следствия
5 п. 3 § 3. Теорема доказана.
Теорема
8.12.
Пусть
функция
![]() кусочно
непрерывна на сегменте
кусочно
непрерывна на сегменте![]() и периодически (с периодом
и периодически (с периодом![]() )
продолжена на всю прямую, и пусть
)
продолжена на всю прямую, и пусть
![]() некоторая точка прямой. Для того, чтобы
тригонометрический ряд Фурье функции
некоторая точка прямой. Для того, чтобы
тригонометрический ряд Фурье функции
![]() сходился
в точке
сходился
в точке
![]() ,достаточно, чтобы существовала кусочно
непрерывная на сегменте
,достаточно, чтобы существовала кусочно
непрерывная на сегменте
![]() и
периодическая (с периодом
и
периодическая (с периодом
![]() )
функция
)
функция![]() ,
обладающая сходящимся в точке
,
обладающая сходящимся в точке
![]() тригонометрическим
рядом Фурье и совпадающая с
тригонометрическим
рядом Фурье и совпадающая с
![]() в
как угодной малой
в
как угодной малой
![]() –
окрестности точки
–
окрестности точки
![]() .
.
Доказательство.
Достаточно применить лемму Римана к
разности
![]() по сегменту
по сегменту![]() и
учесть что из сходимости в точке
и
учесть что из сходимости в точке![]() тригонометрических рядов функций
тригонометрических рядов функций![]() и
и![]() вытекает
сходимость в этой точке и тригонометрического
ряда Фурье функции
вытекает
сходимость в этой точке и тригонометрического
ряда Фурье функции![]() .
Теорема доказана.
.
Теорема доказана.
Теорема
8.12 не устанавливает конкретного вида
условий, обеспечивающих сходимость
тригонометрического ряда Фурье функции
![]() в
точке
в
точке![]() .
Она лишь доказывает, что эти условия
определяются только поведением
.
Она лишь доказывает, что эти условия
определяются только поведением![]() в
как угодно малой окрестности точки
в
как угодно малой окрестности точки
![]() (т.е. имеютлокальный
характер).
(т.е. имеютлокальный
характер).
5.
Равномерная сходимость тригонометрического
ряда Фурье для функции из класса Гёльдера.
В этом и следующем пункте мы уточним
условия, обеспечивающие равномерную
сходимость и сходимость в данной точке
![]() тригонометрического
ряда Фурье.
тригонометрического
ряда Фурье.
Теорема
8.13. Если функция
![]() принадлежит на сегменте
принадлежит на сегменте![]() классу
Гёльдера
классу
Гёльдера![]() с каким угодно положительным показателем
с каким угодно положительным показателем![]() (
(![]() )
и если, кроме того,
)
и если, кроме того,![]() ,
то тригонометрический ряд Фурье функции
,
то тригонометрический ряд Фурье функции![]() сходится
(к этой функции) равномерно на сегменте
сходится
(к этой функции) равномерно на сегменте![]() .
.
Доказательство.
Как
обычно, будем считать, что функция f(x)
периодически (с периодом 2![]() )
продолжена на всю числовую прямую.
Условиеf(
)
продолжена на всю числовую прямую.
Условиеf(![]() )=f(
)=f(![]() )
обеспечивает принадлежность так
продолженной функции классу Гёльдера
)
обеспечивает принадлежность так
продолженной функции классу Гёльдера
![]() на всей прямой.
на всей прямой.
Пусть
х
– любая точка сегмента [-![]() ;
;![]() ].
Умножая обе части равенства (8.56) наf(x)
и вычитая полученное при этом равенство
из (8.55), получим равенство
].
Умножая обе части равенства (8.56) наf(x)
и вычитая полученное при этом равенство
из (8.55), получим равенство
![]()
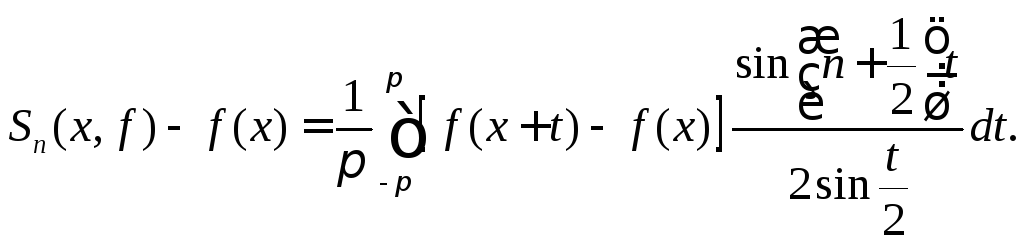 (8.68)
(8.68)
Из
условия принадлежности f(x)
классу Гёльдера
![]() вытекает существование постояннойМ
такой, что
вытекает существование постояннойМ
такой, что
![]() (8.69)
(8.69)
во
всяком случае для всех х
и для всех t
из сегмента [-![]() ;
;![]() ].
].
Фиксируем произвольное ε >0 и по нему δ>0, удовлетворяющее неравенству
![]() .
(8.70)
.
(8.70)
Разбивая
сегмент [-![]() ;
;![]() ]
на сумму отрезка
]
на сумму отрезка![]() и множества
и множества![]() ,
придадим равенству (8.68) следующий вид:
,
придадим равенству (8.68) следующий вид:
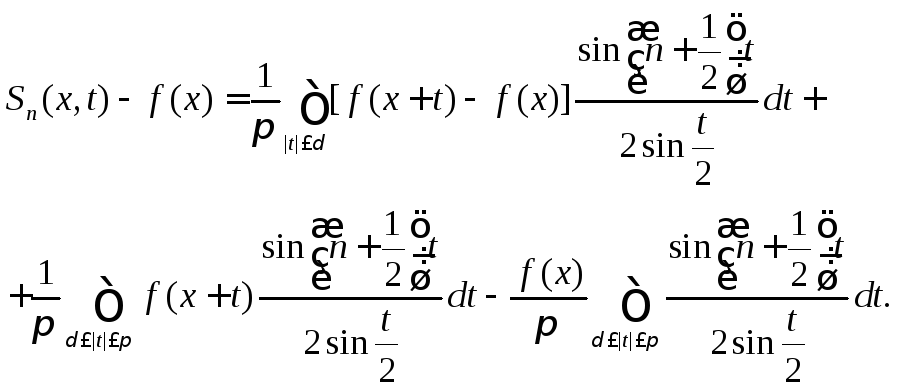 (8.71)
(8.71)
Для оценки первого интеграла в правой части (8.71) воспользуемся неравенством (8.69) и учтем, что
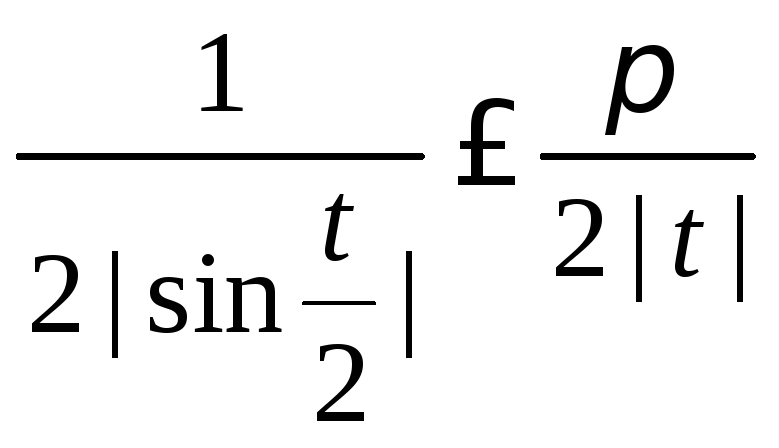
для
всех t
из сегмента [-![]() ;
;![]() ]31).
Таким образом, для любого номера n
и любого x
из сегмента [-
]31).
Таким образом, для любого номера n
и любого x
из сегмента [-![]() ;
;![]() ]
получим
]
получим
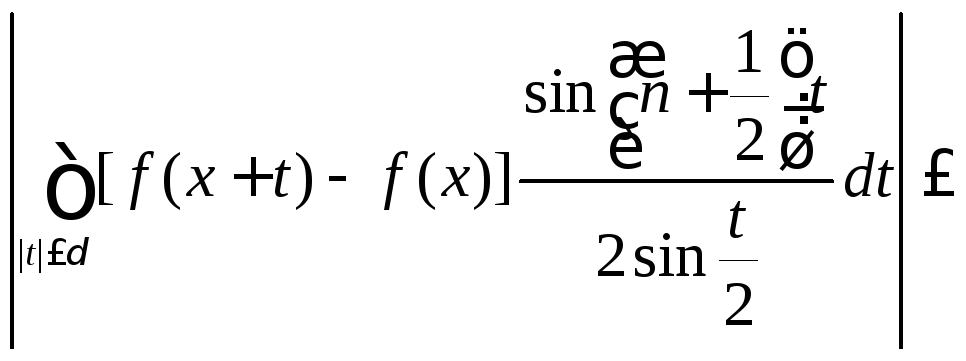
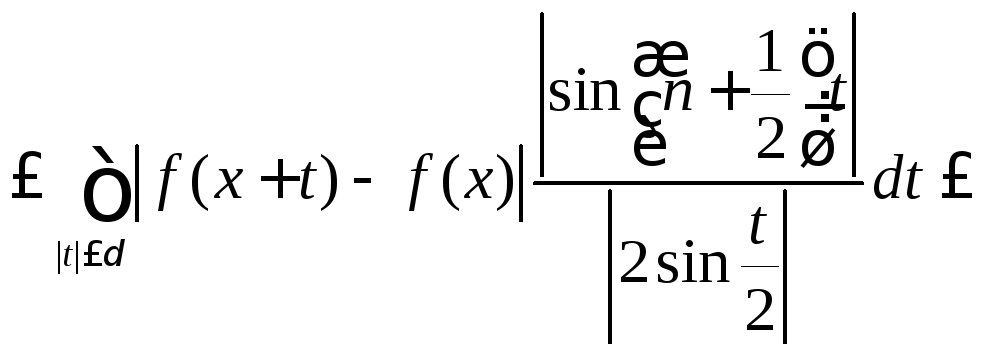
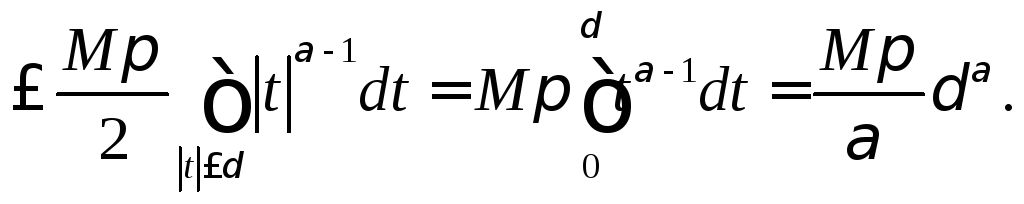
![]()
Отсюда на основании (8.70) для любого номера n и любого x из сегмента
[-![]() ;
;![]() ]
будем иметь оценку
]
будем иметь оценку
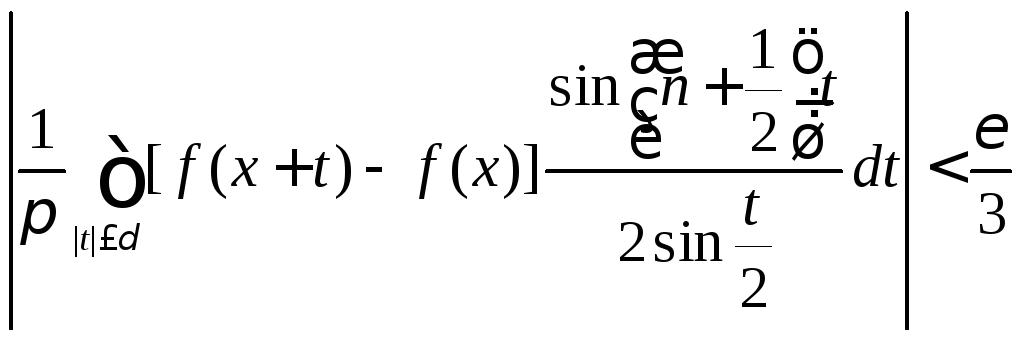 (8.72)
(8.72)
Второй
интеграл в правой части (8.71) с помощью
кусочно непрерывной на сегменте [-![]() ;
;![]() ]
функции (8.67) записывается в виде
]
функции (8.67) записывается в виде
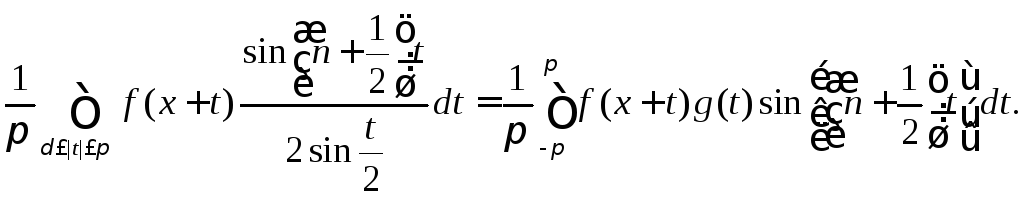
В
силу следствия 4 п. 3 правая часть
последнего равенства при
![]() сходится к нулю равномерно относительноx
на сегменте [-
сходится к нулю равномерно относительноx
на сегменте [-![]() ;
;![]() ].
Поэтому для фиксированного нами
].
Поэтому для фиксированного нами![]() найдется номерN1
такой,
что
найдется номерN1
такой,
что
![]()
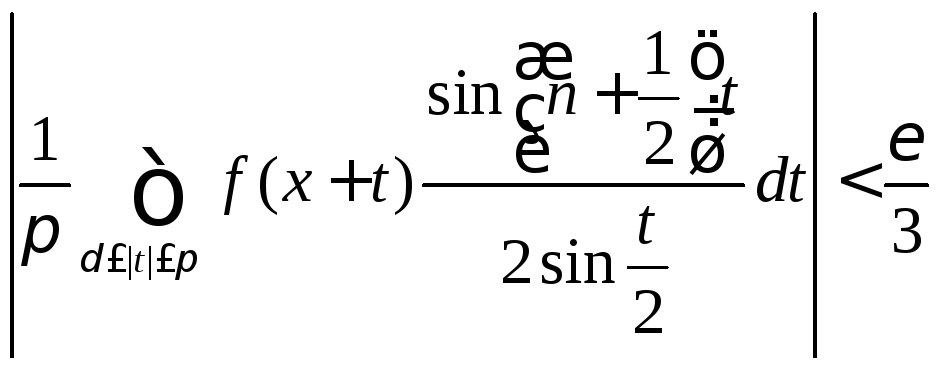 (8.73)
(8.73)
для
всех n![]() N1
и всех x
из сегмента [-
N1
и всех x
из сегмента [-![]() ;
;![]() ].Для
оценки последнего интеграла в правой
части (8.71) заметим, что с помощью кусочно
непрерывной функции (8.67) этот интеграл
записывается в виде
].Для
оценки последнего интеграла в правой
части (8.71) заметим, что с помощью кусочно
непрерывной функции (8.67) этот интеграл
записывается в виде
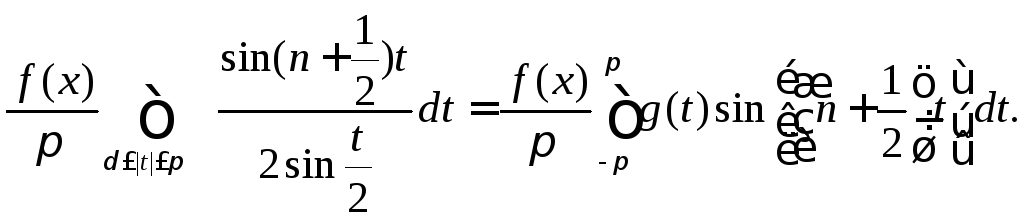
Интеграл,
стоящий в правой части последнего
равенства, при
![]() сходится к нулюв силу в силу все того
же следствия 4 п. 3 (достаточно применить
это следствие к функции
сходится к нулюв силу в силу все того
же следствия 4 п. 3 (достаточно применить
это следствие к функции![]() ).
Учитывая также, что функцияf(x)
во всяком случае ограничена на сегменте
[-
).
Учитывая также, что функцияf(x)
во всяком случае ограничена на сегменте
[-![]() ;
;![]() ],
получим, что для фиксированного нами
произвольного
],
получим, что для фиксированного нами
произвольного![]() найдется номерN2
такой, что
найдется номерN2
такой, что
 (8.74)
(8.74)
для
всех n![]() N2
и всех x
из сегмента [-
N2
и всех x
из сегмента [-![]() ;
;![]() ].
].
Обозначив
через N
наибольший из двух номеров N1
и
N2,
в силу (8.71) – (8.74) получим, что для
фиксированного нами произвольного
![]() найдется номерN
такой, что
найдется номерN
такой, что
![]()
для
всех n![]() N
и всех x
из сегмента [-
N
и всех x
из сегмента [-![]() ;
;![]() ].
Теорема доказана.
].
Теорема доказана.
Замечание
1. Очевидно,
что в условиях теоремы 8.13 тригонометрический
ряд Фурье сходится равномерно не только
не только на сегменте [-![]() ;
;![]() ],
но и на всей прямой (к функции, являющейся
периодическим (с периодом 2
],
но и на всей прямой (к функции, являющейся
периодическим (с периодом 2![]() )
продолжением функцииf(x)
на всю прямую).
)
продолжением функцииf(x)
на всю прямую).
Замечание
2.
Отметим, что при оценке интегралов
(8.73) и (8.74) мы использовали лишь кусочную
непрерывность (и вытекающую из нее
ограниченность) функции f(x)
на сегменте [-![]() ;
;![]() ]
(принадлежностьf(x)
классу Гёльдера
]
(принадлежностьf(x)
классу Гёльдера
![]() при оценке этих интегралов не
использовалась).
при оценке этих интегралов не
использовалась).
В
условиях теоремы 8.13 после периодического
(с периодом 2![]() )
продолжения функцияf(x)
оказалась принадлежащей классу Гёльдера
)
продолжения функцияf(x)
оказалась принадлежащей классу Гёльдера
![]() на
всей числовой прямой.
Естественно возникает вопрос о поведении
тригонометрического ряда Фурье функции
f(x),
принадлежащей классу Гёльдера
на
всей числовой прямой.
Естественно возникает вопрос о поведении
тригонометрического ряда Фурье функции
f(x),
принадлежащей классу Гёльдера
![]() только
на некотором сегменте [a,
b],
а всюду вне этого сегмента удовлетворяющей
лишь обычному требованию кусочной
непрерывности. Ответ на этот вопрос
дает следующая теорема.
только
на некотором сегменте [a,
b],
а всюду вне этого сегмента удовлетворяющей
лишь обычному требованию кусочной
непрерывности. Ответ на этот вопрос
дает следующая теорема.
Теорема
8.14.
Пусть
функция f(x)
кусочно непрерывна на сегменте [-![]() ;
;![]() ]и
периодически (с периодом 2
]и
периодически (с периодом 2![]() )продолжена
на всю числовую прямую.
)продолжена
на всю числовую прямую.
Пусть
далее на некотором сегменте [а,b],
имеющем длину, меньшую 2![]() ,эта
функция принадлежит классу Гёльдера
,эта
функция принадлежит классу Гёльдера
![]() с произвольным положительным показателем
с произвольным положительным показателем
![]() (0<
(0<![]()
![]() 1).Тогда
для любого
1).Тогда
для любого
![]() из
интервала 0<
из
интервала 0<![]() <(b-a)/2
<(b-a)/2
тригонометрический
ряд Фурье функции f(x)
сходится (к этой функции) равномерно
на сегменте [а+![]() ,b-
,b-![]() ].
].
Доказательство.
Построим функцию g{x),
которая
на сегменте [а,
b]
совпадает
с f(x),
на
сегменте [b,
a+2![]() ]
является линейной функцией видаАх+В,
обращающейся
в f(b)
при
х=b
и
в f
(а) при
x=а+2
]
является линейной функцией видаАх+В,
обращающейся
в f(b)
при
х=b
и
в f
(а) при
x=а+2![]() 33),
и которая периодически (с периодом 2
33),
и которая периодически (с периодом 2![]() )
продолжена с сегмента[а,
а+2
)
продолжена с сегмента[а,
а+2![]() ]
на
всю прямую (на рис. 8.1 жирная линия
изображает график функции f(x),
а
штриховая линия —график построенной
по ней функции g(x)).
]
на
всю прямую (на рис. 8.1 жирная линия
изображает график функции f(x),
а
штриховая линия —график построенной
по ней функции g(x)).
Очевидно, что построенная нами функция g(x) удовлетворяет условию
g(-![]() )=g(
)=g(![]() )
и принадлежит классу Гёльдера
)
и принадлежит классу Гёльдера
![]() (с тем же положительным показателем
а, что и f(x))
на
всей прямой34).
(с тем же положительным показателем
а, что и f(x))
на
всей прямой34).

Рис. 8.1
В
силу теоремы 8.13 и замечания 1
тригонометрический ряд Фурье функции
g(x)
сходится
равномерно на всей числовой прямой, а
поэтому в силу теоремы 8.11 тригонометрический
ряд Фурье функции f(x)
при
любом
![]() из интервала 0<
из интервала 0<![]() <(b-а)/2
сходится
(к этой функции) равномерно на сегменте
[а+
<(b-а)/2
сходится
(к этой функции) равномерно на сегменте
[а+![]() ,b-
,b-![]() ].
Теорема доказана.
].
Теорема доказана.
Замечание
4.
Утверждение теоремы 8.14 остается
справедливым и для сегмента [а,
b],
имеющего длину, равную
2![]() (т. е. для случаяb=а+2
(т. е. для случаяb=а+2![]() ,
но в этом случае при доказательстве
теоремы следует, фиксировав произвольное
,
но в этом случае при доказательстве
теоремы следует, фиксировав произвольное
![]() из интервала 0<
из интервала 0<![]() <
<![]() ,
взять функциюg(x)
совпадающей
с f(x)
на
сегменте [а+
,
взять функциюg(x)
совпадающей
с f(x)
на
сегменте [а+![]() /2,
а+2
/2,
а+2![]() -
-![]() /2],
линейной на сегменте [a+2
/2],
линейной на сегменте [a+2![]() -
-![]() /2,
a+2
/2,
a+2![]() +
+![]() /2]
и периодически (с периодом 2
/2]
и периодически (с периодом 2![]() )
продолженной с сегмента [а+
)
продолженной с сегмента [а+![]() /2,
а+2
/2,
а+2![]() +
+![]() /2]
на всю числовую прямую. Если же сегмент
[а,b]
имеет
длину, превосходящую
2
/2]
на всю числовую прямую. Если же сегмент
[а,b]
имеет
длину, превосходящую
2![]() ,
то из принадлежностиf(x)
классу
Гёльдера
,
то из принадлежностиf(x)
классу
Гёльдера
![]() на
этом сегменте и из условия периодичности
f(х)
(с
периодом 2
на
этом сегменте и из условия периодичности
f(х)
(с
периодом 2![]() )
вытекает, чтоf(x)
принадлежит
классу
)
вытекает, чтоf(x)
принадлежит
классу
![]() на всей прямой, т. е. в этом случае мы
приходим к теореме 8.13.
на всей прямой, т. е. в этом случае мы
приходим к теореме 8.13.
6. О сходимости тригонометрического ряда Фурье кусочно гёльдеровой функции.
Определение
1.
Будем
называть функцию f(x)
кусочно
гёльдеровой
на сегменте
[а,b],
если эта функция кусочно непрерывна
на сегменте [а,b]
и
если этот сегмент при помощи конечного
числа точек a=x0<x1<x2<
... <хп=b
разбивается на частичные сегменты
[хк-1,
хк]
(k=1,
2,..., n),
на
каждом из которых функция f(x)
принадлежит классу Гёльдера![]()
![]() с
некоторым положительным показателем
с
некоторым положительным показателем
![]() (0<
(0<![]()
![]() 1).При
этом при определении класса Гёльдера
на частичном сегменте [хк-1,
хк]
в качестве значений функции на концах
сегмента следует брать предельные
значения
1).При
этом при определении класса Гёльдера
на частичном сегменте [хк-1,
хк]
в качестве значений функции на концах
сегмента следует брать предельные
значения
![]() и
и
![]() 35).
35).
Иными словами, область задания всякой кусочно гёльдеровой функции распадается на конечное число не имеющих общих внутренних точек сегментов, на каждом из которых эта функция принадлежит классу Гёльдера с некоторым положительным показателем.
Каждый из этих сегментов мы будем называть участком гладкости функции.
Определение 2. Будем называть функцию f(x) кусочно гладкой на сегменте [а,b], если эта функция кусочно непрерывна на сегменте [а,b] и имеет на этом сегменте кусочно непрерывную производную36), т. е. если функция f(x) кусочно непрерывна на сегменте [а,b] и ее производная f'(x) существует и непрерывна всюду на этом сегменте, за исключением, быть может, конечного числа точек, в каждой из которых функция f'(x) имеет конечные правое и левое предельные значения.
Ясно, что всякая кусочно гладкая на сегменте [а,b] функция является на этом сегменте кусочно гёльдеровой.
Теорема
8.15.
Пусть
кусочно гёльдеровая на сегменте [-![]() ;
;![]() ]
функция
f(x)
периодически (с периодом 2
]
функция
f(x)
периодически (с периодом 2![]() )продолжена
на
всю прямую.
Тогда
тригонометрический ряд Фурье функции
f(х)
сходится в каждой точке х прямой к
значению f(x)=[f(x+0)
+ f(x-0)]/2,
причем
сходимость этого ряда является раеномерной
на каждом фиксированном сегменте,
лежащем внутри участка гладкости
функции f(x).
)продолжена
на
всю прямую.
Тогда
тригонометрический ряд Фурье функции
f(х)
сходится в каждой точке х прямой к
значению f(x)=[f(x+0)
+ f(x-0)]/2,
причем
сходимость этого ряда является раеномерной
на каждом фиксированном сегменте,
лежащем внутри участка гладкости
функции f(x).
Доказательство. Утверждение теоремы о равномерной сходимости на каждом фиксированном сегменте, лежащем внутри участка гладкости, сразу вытекает из теоремы 8.14. Отсюда же вытекает и сходимость тригонометрического ряда Фурье функции f(x) в каждой внутренней точке участка гладкости функции f(х)37). Остается доказать сходимость тригонометрического ряда Фурье функции f(x) в каждой точке соединения двух участков гладкости.
Фиксируем одну из таких точек и обозначим ее через х. Тогда найдутся постоянные М1 и М2 такие, что при любом достаточно малом положительном t будет справедливо неравенство
![]()
![]() ,
(8.75)
,
(8.75)
а при любом достаточно малом отрицательном t — неравенство
![]()
![]() .
(8.76)
.
(8.76)
Обозначим
через М
наибольшее
из чисел М1
и
М2,
а
через
![]()
![]() наименьшее
из чисел
наименьшее
из чисел
![]() и
и![]() .
Тогда при |t|
.
Тогда при |t|![]() 1
в правой части каждого из неравенств
(8.75) и (8.76) можно писать
1
в правой части каждого из неравенств
(8.75) и (8.76) можно писать![]() .
Фиксируем теперь произвольное
.
Фиксируем теперь произвольное
 и по нему
и по нему![]() ,
удовлетворяющее
неравенству (8.70) и настолько малое, что
при |t|
,
удовлетворяющее
неравенству (8.70) и настолько малое, что
при |t|![]() справедливы
оба неравенства (8.75) и (8.76) и в правой
части этих
неравенств можно брать число
справедливы
оба неравенства (8.75) и (8.76) и в правой
части этих
неравенств можно брать число
![]() .
Повторяя
рассуждения,
проведенные при доказательстве теоремы
8.13, мы придем к равенству
(8.71), и для доказательства теоремы нам
остается убедиться, что в фиксированной
нами точке х
справедливы
оценки
(8.72), (8.73) и (8.74). В замечании 2 п. 5 мы
отметили, что оценки
(8.73) и (8.74) справедливы для любой только
кусочно непрерывной
и периодической (с периодом 2
.
Повторяя
рассуждения,
проведенные при доказательстве теоремы
8.13, мы придем к равенству
(8.71), и для доказательства теоремы нам
остается убедиться, что в фиксированной
нами точке х
справедливы
оценки
(8.72), (8.73) и (8.74). В замечании 2 п. 5 мы
отметили, что оценки
(8.73) и (8.74) справедливы для любой только
кусочно непрерывной
и периодической (с периодом 2![]() )
функции. Остается
доказать
справедливость для всех номеров n
оценки (8.72).
)
функции. Остается
доказать
справедливость для всех номеров n
оценки (8.72).
Так
как
![]() и38)
и38)
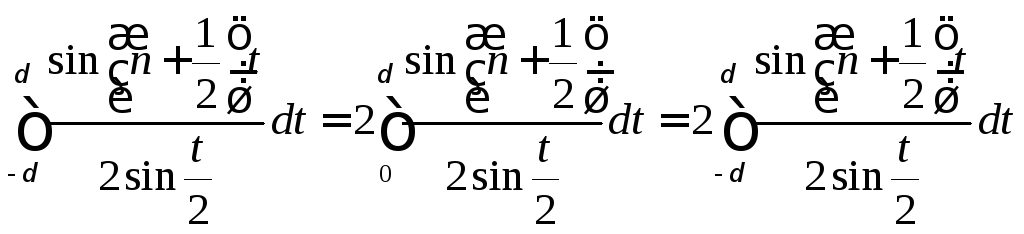 ,
,
то интеграл, стоящий в левой части (8.72), можно переписать так

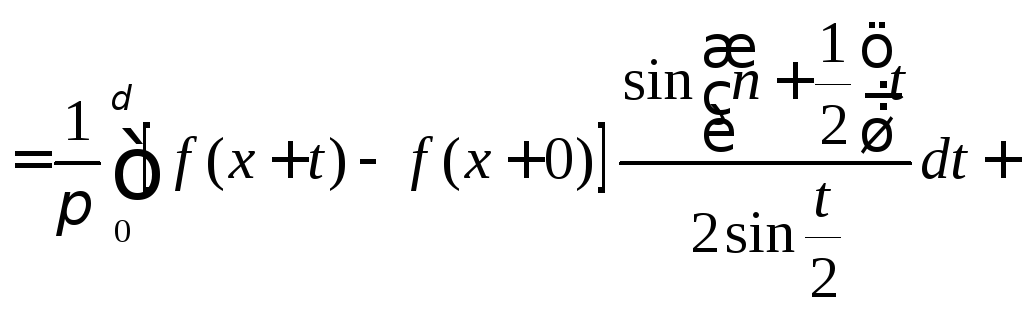
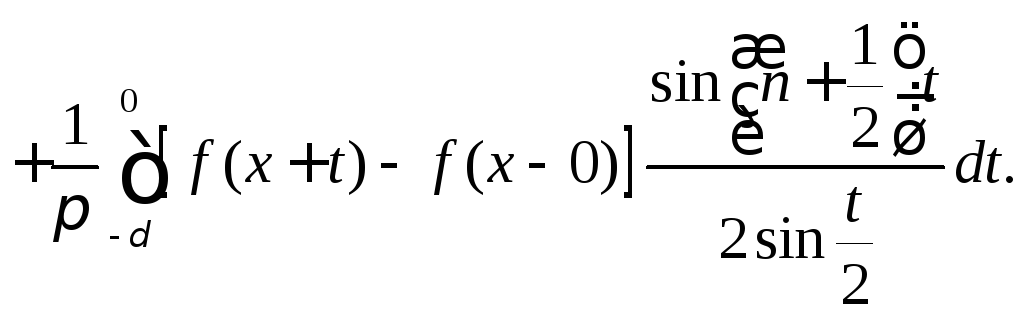 (8.77)
(8.77)
Для
оценки интегралов, стоящих в правой
части (8.77), воспользуемся
неравенствами (8.75) и (8.76), беря в правой
части этих
неравенств число
![]() .
Учитывая уже применявшуюся при
доказательстве
теоремы 8.13 оценку
.
Учитывая уже применявшуюся при
доказательстве
теоремы 8.13 оценку
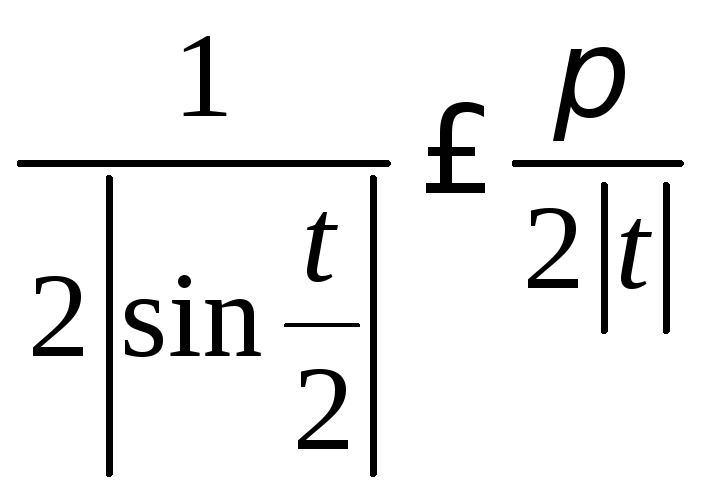
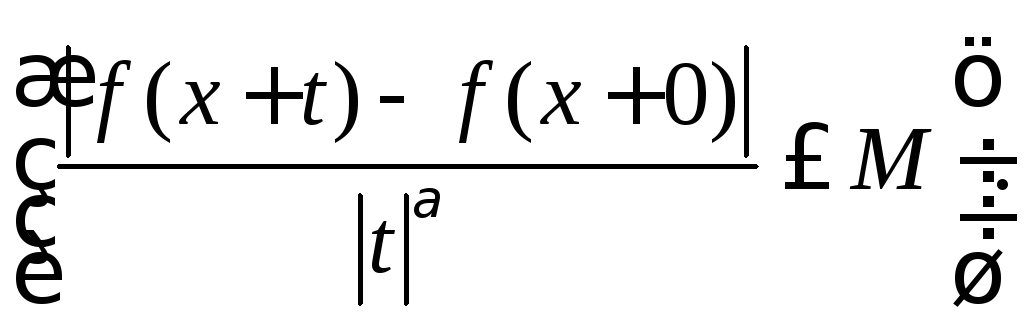 (при
(при
![]() )
)
и неравенство (8.70), будем иметь
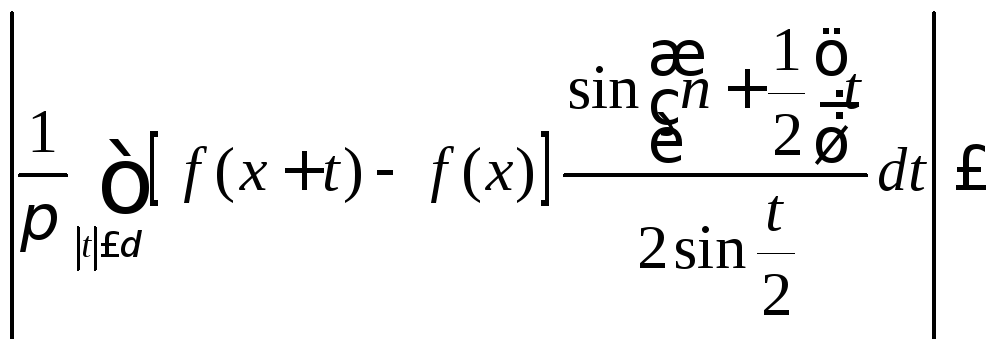
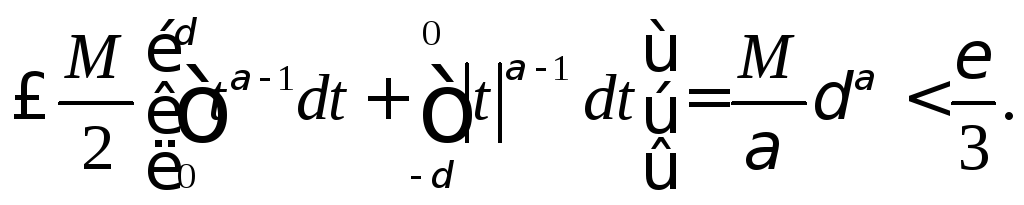
Оценка (8.72), а с ней и теорема доказаны.
Следствие
1.
Утверждение
теоремы 8.15
будет
тем более справедливо, если в ее
формулировке вместо кусочно гёльдеровой
взять кусочно гладкую (на сегменте
[-![]() ;
;![]() ])
функцию, периодически (с периодом
2
])
функцию, периодически (с периодом
2![]() )
продолженную на всю прямую.
)
продолженную на всю прямую.
Для
формулировки еще одного следствия
введем новое понятие. Пусть 0<![]() 1.
1.
Определение
3.
Будем
говорить, что функция f(x)
удовлетворяет
в данной точке
х справа (слева) условию Гёльдера
порядка
![]() , если функцияf(x)
имеет в точке х правое (левое) предельное
значение и если существует такая
постоянная М, что для всех достаточно
малых положительных (отрицательных) t
справедливо
неравенство
, если функцияf(x)
имеет в точке х правое (левое) предельное
значение и если существует такая
постоянная М, что для всех достаточно
малых положительных (отрицательных) t
справедливо
неравенство
![]()
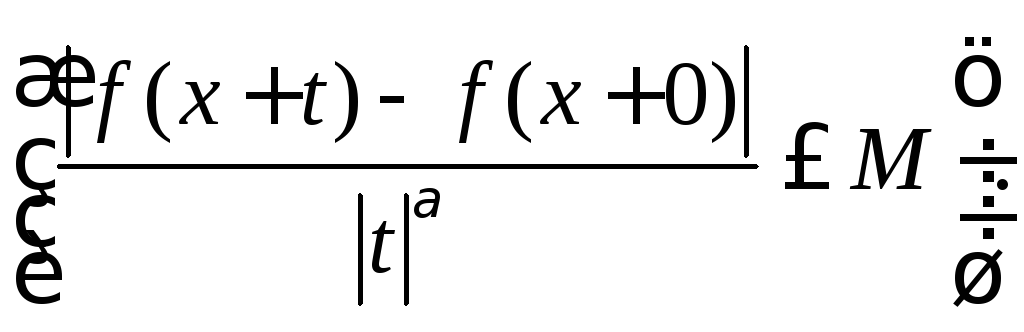
![]()
Очевидно, что если функция f(x) имеет в данной точке х правую (левую) производную, понимаемую как предел
![]()
![]()
то
функция f(x)
заведомо
удовлетворяет в этой точке х
справа
(слева) условию Гёльдера любого порядка
![]() 1.
1.
Следствие
2 (условие сходимости тригонометрического
ряда Фурье в данной точке).
Для
того чтобы тригонометрический ряд Фурье
кусочно непрерывной и периодической
(с периодом 2![]() )
функции
f(x)
сходился в данной точке х числовой
прямой, достаточно, чтобы функция
f(x)
удовлетворяла в точке х справа условию
Гёльдера какого-либо положительного
порядка
)
функции
f(x)
сходился в данной точке х числовой
прямой, достаточно, чтобы функция
f(x)
удовлетворяла в точке х справа условию
Гёльдера какого-либо положительного
порядка
![]() и в точке х слева условию Гёльдера
какого-либо положительного порядка
и в точке х слева условию Гёльдера
какого-либо положительного порядка![]() (и тем более достаточно, чтобы функцияf(x)
имела в точке х правую и левую производные).
(и тем более достаточно, чтобы функцияf(x)
имела в точке х правую и левую производные).
Доказательство.
Достаточно заметить, что из того, что
функция f(x)
удовлетворяет
в точке х
справа
(слева) условию Гёльдера порядка
![]() ,
(порядка
,
(порядка
![]() ),
вытекает существование постоянной
М1
(постоянной
М2)
такой,
что для всех достаточно малых
положительных (отрицательных) t
справедливо
неравенство (8.75) (неравенство (8.76)). Так
как доказательство теоремы 8.15 использует
лишь неравенства (8.75) и (8.76) и кусочную
непрерывность и периодичность f(x),
то
утверждение следствия 2 верно.
),
вытекает существование постоянной
М1
(постоянной
М2)
такой,
что для всех достаточно малых
положительных (отрицательных) t
справедливо
неравенство (8.75) (неравенство (8.76)). Так
как доказательство теоремы 8.15 использует
лишь неравенства (8.75) и (8.76) и кусочную
непрерывность и периодичность f(x),
то
утверждение следствия 2 верно.
Пример. Не вычисляя коэффициентов Фурье функции
![]()
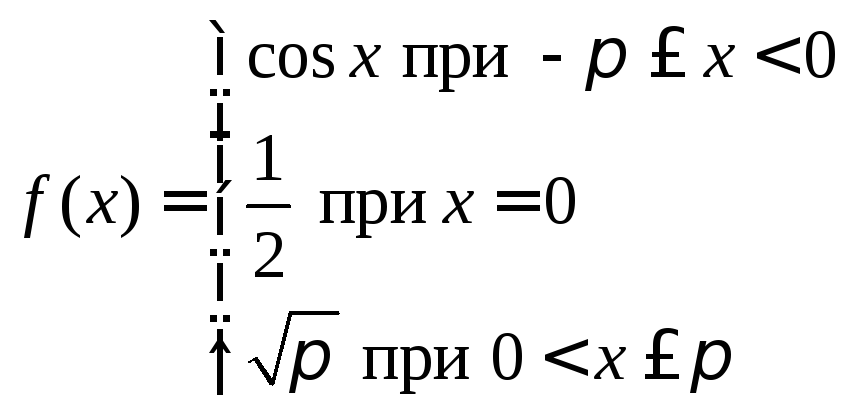
![]()
можно
утверждать, что тригонометрический ряд
Фурье этой функции сходится в точке х=0
к
значению
![]() ,
так как функцияf(x)
имеет
в этой точке левую производную и
удовлетворяет в этой точке справа
условию Гёльдера порядка
,
так как функцияf(x)
имеет
в этой точке левую производную и
удовлетворяет в этой точке справа
условию Гёльдера порядка
![]() =
=![]() .
.
Заключительные
замечания. 1°.
При решении ряда конкретных
задач приходится раскладывать функцию
в тригонометрический
ряд Фурье не на сегменте [-![]() ;
;![]() ],
а
на сегменте [-l,l],
где l
–
произвольное положительное число. Для
перехода к такому случаю достаточно во
всех проведенных выше рассуждениях
заменить
переменную х
на
],
а
на сегменте [-l,l],
где l
–
произвольное положительное число. Для
перехода к такому случаю достаточно во
всех проведенных выше рассуждениях
заменить
переменную х
на
![]() .
Конечно,
при такой линейной замене
переменной останутся справедливыми
все установленные нами результаты,
которые будут относиться к тригонометрическому
ряду
Фурье
.
Конечно,
при такой линейной замене
переменной останутся справедливыми
все установленные нами результаты,
которые будут относиться к тригонометрическому
ряду
Фурье
![]() (8.85)
(8.85)
со следующими выражениями для коэффициентов Фурье:
![]()
![]()
![]()
![]() (8.86)
(8.86)
n=1, 2, ...
Мы
не будем заново формулировать все
установленные теоремы,
а лишь отметим, что во всех формулировках
сегмент [-![]() ;
;![]() ]
следует
заменить сегментом [-l,l],
а период 2
]
следует
заменить сегментом [-l,l],
а период 2![]() — периодом 2l.
— периодом 2l.
2°. Из вида (8.86) тригонометрических коэффициентов Фурье вытекает, что для четной функции f(x) равны нулю все коэффициенты bк (k=1, 2, ...), а для нечетной функции f(x) равны нулю все коэффициенты ak (k=0, 1, 2, ...). Таким образом, четная функция f(x) раскладывается в тригонометрический ряд Фурье только по косинусам:
![]()
![]()
а нечетная функция f(x) раскладывается в тригонометрический ряд Фурье только по синусам:
![]()
![]()
3°.Приведем весьма часто употребляемую комплексную форму записи тригонометрического ряда Фурье (8.85). Используя соотношения (см. п. 3 § 7 гл. 2)
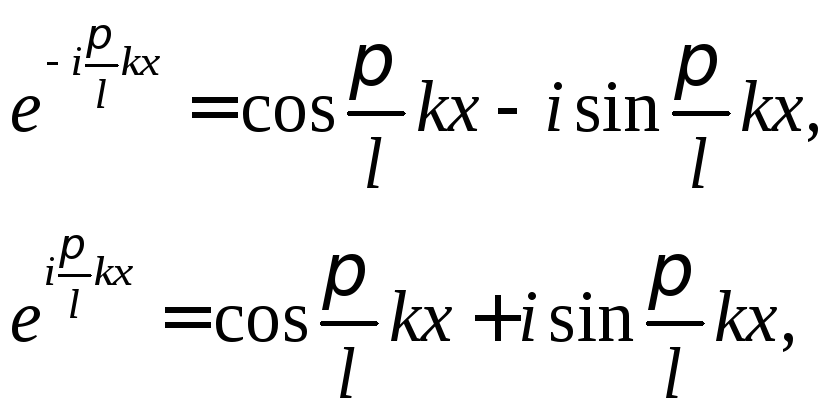
легко убедиться в том, что тригонометрический ряд Фурье (8.85) с коэффициентами Фурье (8.86) приводится к виду
![]() ,
(8.87)
,
(8.87)
в котором комплексные коэффициенты сk имеют вид
![]()
и выражаются через коэффициенты (8.86) по формулам
![]()
![]()
![]() (k=1,2,…)
(k=1,2,…)
