§4. Предел функции m переменных

Пусть числовая функция f определена на множестве . Будем использовать обозначениеили.

Пусть точка - предельная точка множестваX.

Определение 1.(предела функции по Гейне)

Число a называется пределом функции f в точке , если для любой сходящейся к точкепоследовательноститочек множестваX, все элементы которой отличны от , числовая последовательность значений функциисходится к числуa.

Определение 1*.(предела функции в точке по Коши)

Число a называется пределом функции f в точке , если

Для обозначения предела используется следующая символика:

.

Доказательство эквивалентности определения 1 и 1* проводится точно так же, как и для функции одной переменной.

Введем понятие предела функции f при . Для этого положим, что множествоX для любого имеет хотя бы один элемент, лежащий вне шара радиусас центром в точке. Ограничимся определением по Коши.

Определение 2.

Число a называется пределом функции f при , если .

Так же, как и для функции одной переменной, доказывается теорема 1.

Теорема 1. Если , то

,

,

при дополнительном требовании, что и функцияg в ноль не обращается.

Определение 3.

Будем говорить, что функция f удовлетворяет условию Коши в точке (соответственно при), если

Теорема 2. (Критерий Коши существования предела функции в точке).

Для того чтобы функция f имела конечный предел в точке [при], необходимо и достаточно, чтобы эта функция удовлетворяла в точке[при] условию Коши.

Доказательство этой теоремы полностью идентично доказательству критерия Коши для функции одной переменной.

§5. Непрерывность функции m переменных.

Приведем два эквивалентных определения непрерывности функции в точке.

Определение 1.(непрерывности функции в точке по Гейне)

Функция f называется непрерывной в точке , если для любой сходящейся к точкепоследовательноститочек множестваX числовая последовательность значений этой функции сходится к числу.

Определение 1*.(непрерывности функции в точке по Коши)

Функция f называется непрерывной в точке , если

Сопоставляя эти определения с определениями предела функции в точке, нетрудно прийти к выводу:

Функция f непрерывна в точке , являющейся предельной точкой множестваX, тогда и только тогда, когда .

Определение 2.

Функция f называется непрерывной на множестве X, если она непрерывна в каждой точке этого множества.

Основные свойства непрерывных функций:

1. Если функции f и g непрерывны в точке 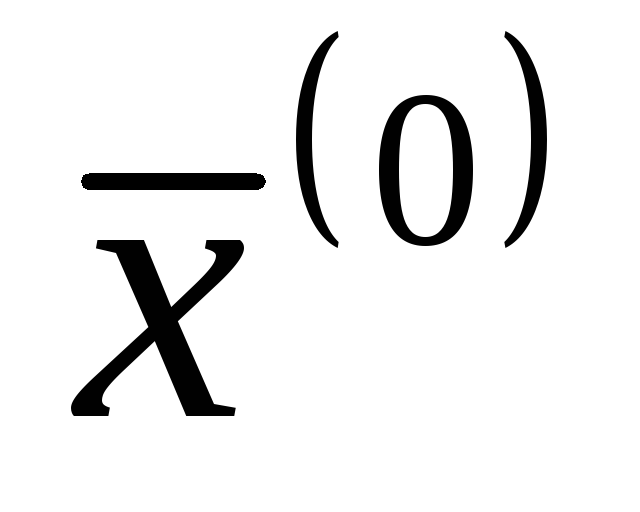, то функци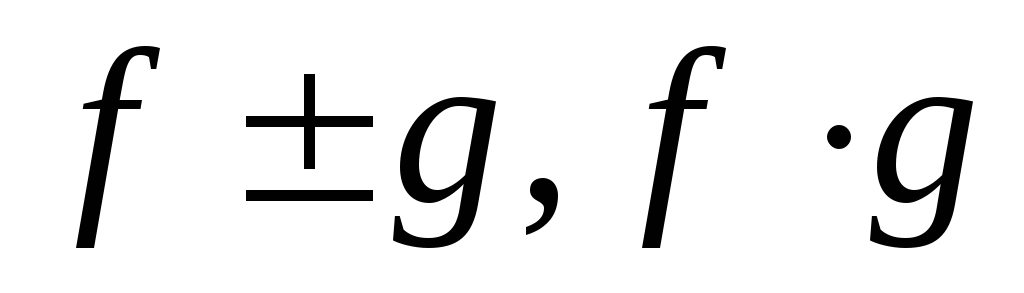ии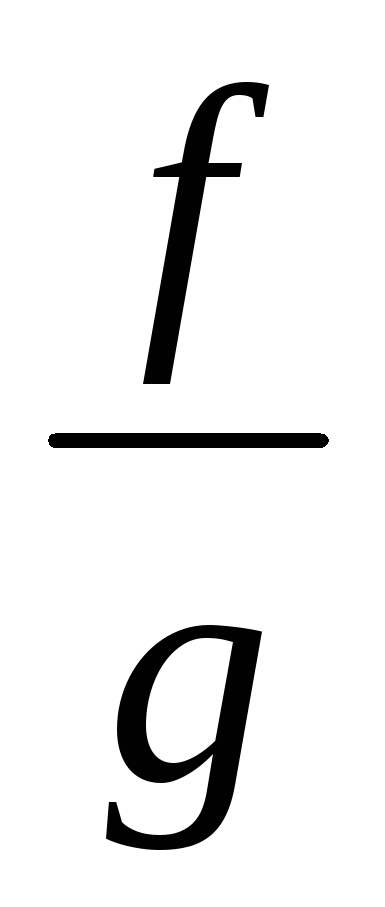также непрерывны в точке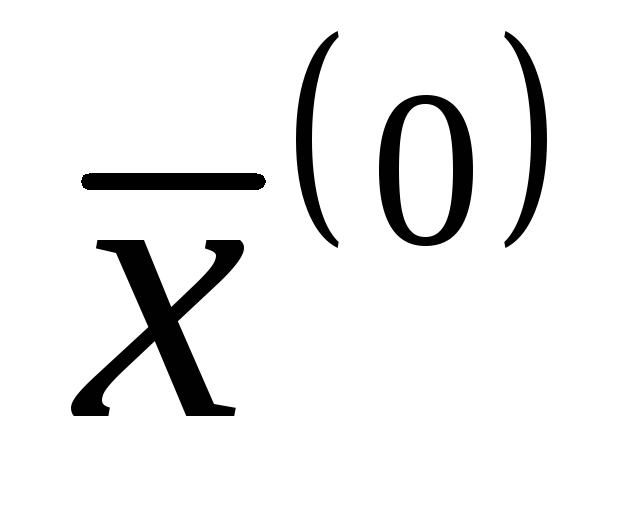(в случае частного нужно дополнительно потребовать, чтобыg не обращалась в 0). Это утверждение вытекает из теоремы 1 предыдущего параграфа.

2. Непрерывность сложной функции.

Пусть функции

непрерывны в точке , а функциянепрерывна в точке, где,i =1,2,…,m. Тогда сложная функция непрерывна в точке.

Доказательство. Пусть последовательность . Тогда в силу непрерывности функцийв точкеi =1,2,…,m, , а в силу непрерывности функцииf в точке , а в силу непрерывности функцииf в точке . Но это и означает, что, то есть сложная функциянепрерывна в точке. Свойство 2 доказано.

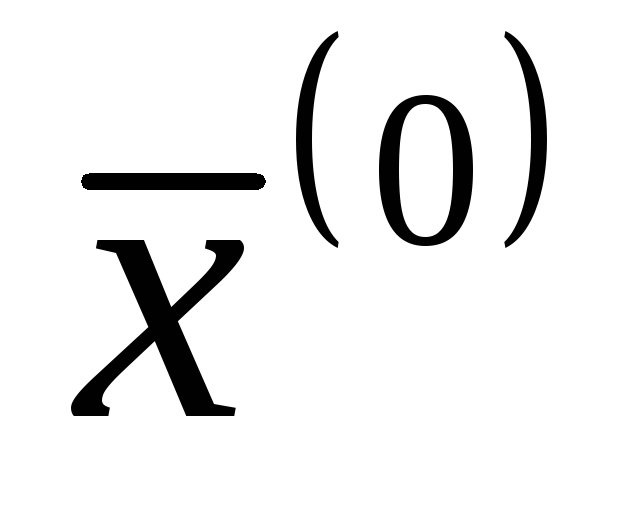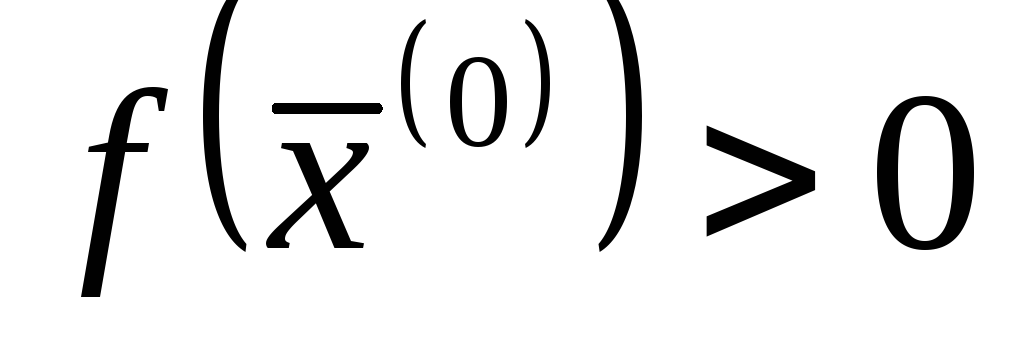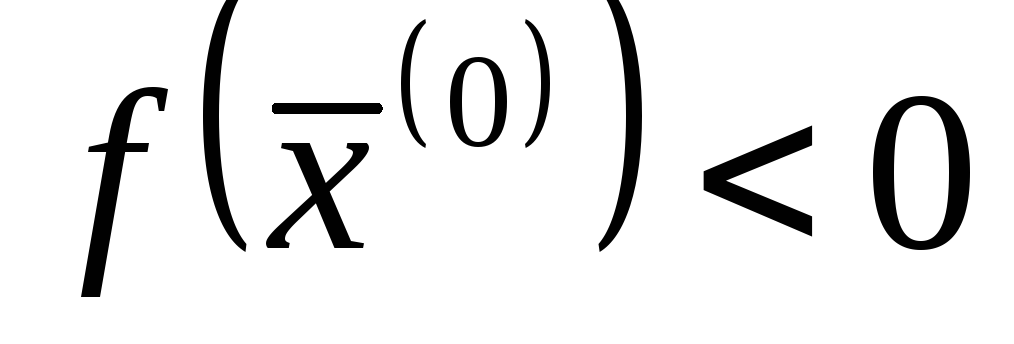3. Теорема об устойчивости знака непрерывной функции. Теорема. Если функция f непрерывна в точке и(), то

().

Доказательство этой теоремы, как и в случае функций одной переменной, почти непосредственно вытекает из определения Коши.

4. Теорема о прохождении непрерывной функции через любое промежуточное значение.

Теорема. Пусть функция f непрерывна на связном множестве X, ,,c – любое число, заключенное между и. Тогда на любой непрерывной кривойL, соединяющей точки ии лежащей в множествеX, найдется точка такая, что .Доказательство. Пусть ,- уравнения непрерывной кривойL; соединяющей точки ии лежащей в множествеX. На отрезке определена сложная функцияодной переменнойt. Эта функция непрерывна на отрезке. В силу теоремы принимает значение c в некоторой . Другими словами функцияf принимает значение c в точке . Теорема доказана.

5. Свойства функции непрерывной на замкнутом ограниченном множестве.

Теорема (первая теорема Вейерштрасса).

Если функция f непрерывна на ограниченном замкнутом множестве X, то она ограничена на нем. Доказательство. Проведем методом от противного. Пусть функция f неограниченна на X. Тогда выделим последовательность точек , для которых. В силу теоремы Больцано – Вейерштрасса из нее можно выделить подпоследовательность, предел которойпринадлежит множествуX( так как X замкнуто). Очевидно, что последовательность неограниченна. С другой стороны в силу непрерывности функцииf в точке эта последовательность. Полученное противоречие доказывает теорему.

Теорема (вторая теорема Вейерштрасса).

Если функция f непрерывна на ограниченном замкнутом множестве X, то она достигает на этом множестве наибольшего и наименьшего значений. Доказательство почти дословно повторяет доказательство второй теоремы Вейерштрасса для функции одной переменной.

Определение 3. Функция f называется равномерно непрерывной на множестве X, если

.

Аналогично случаю одной переменной доказывается теорема Кантора. Теорема Кантора. Непрерывная на ограниченном замкнутом множестве функция равномерно непрерывна на нем.